Densitet och Tryck Fysik1: Skillnad mellan sidversioner

Från Wikiskola
Hoppa till navigering Hoppa till sök
VisuellWikitext
 
(109 mellanliggande sidversioner av samma användare visas inte)
Rad 1: Rad 1:
En simulering om gas i en behållare
=== Konvertera till SI-enheter ===
Som i all fysik är det nödvändigt att göra om de värden du får till SI-enheter innan du sätter in dem i formler och gör beräkningar. När du arbetar med tryck är det extra viktigt.


.
Antag att du behöver konvertera 24 dm<sup>3</sup> till m<sup>3</sup>. Hur gör du då?


.
Det är enkelt om du använder Wolfram Alpha. Skriv till exempel 1 dm^3 i inmatningsrutan så får du se.


.
Eller pröva att göra om 740 mmHg till bar.


Knappen har tyväär hamnat fel på något mysko sätt.
== Densitet ==


Vet ej varför.
Formeln för densiteten är:


..
ρ = m / V
där ρ är densiteten,  m är massan och V är volymen


..
=== Densitetstabell ===
[[Fil:Några_densiteter.png|right]]


En liten densitets-[[tabell med riktiga värden]]?


Fullständig tabell över grundämnenas densitet finns här: {{enwp|Densities_of_the_elements_(data_page)}}


=== Konvertera till SI-enheter ===
'''Tänk på''' att SI-enheten för densitet är kg/m<sup>3</sup>


Som i all fysik är det nödvändigt att göra om de värden du får till SI-enheter innan du sätter in dem i formler och gör beräkningar. När du arbetar med tryck är det extra viktigt.
1 g/cm<sup>3</sup> = 1000 kg/m<sup>3</sup>


Antag att du behöver konvertera 24 dm<sup>3</sup> till m<sup>3</sup>. Hur gör du då?
{{clear}}
 
En enkel väg är att använda denna widget. Du behöver bara skriva in värdet som ska konverteras och den enhet du vill få det konverterat till,
 
'''Exempel''': skriv 24 dm3 och m3 i respektive ruta.
 
{{#widget:WolframAlpha|id=6246bee639c7a7b11a08e34dd3cc6|theme=green|output=lightbox}}
 
Eller pröva att göra om 740 mmHg till bar.


== Densitet ==
=== Uppgift ===


Formeln för densiteten är:
{{uppgruta|'''Beräkna massan'''


p = m / V
Kolla i formelsamlingen. Hitta grundämnet med högst densitet.
där p är densiteten,  m är massan och V är volymen


=== Densitetstabell ===
Hur mycket väger ett klot med radien 2 cm av det ämnet?


En [[tabell med riktiga värden]]?
}}
{{uppgruta| '''Flyter is på olja?'''


=== Rapport ===
Testa hemma.


Läs mer här om att [[skriva labbrapport]]
Läs på hos [http://school.chem.umu.se/Experiment/P217 ResursCentrum för Kemi]
}}


== Tryck mellan fasta kroppar, sid 105-106 ==
== Tryck mellan fasta kroppar, sid 105-106 ==
Rad 55: Rad 54:
  A är arean i m<sup>2</sup>
  A är arean i m<sup>2</sup>


'''Omvandling av tryckenheter'''
=== Tryckenheter ===


''Tabellen kommer från [http://sv.wikipedia.org/wiki/Tryck Wikipedia].''
{{:Omvandling_av_tryckenheter}}


{|border="1" cellspacing="0"
|+Omvandlingstabell för tryckenheter
|-
!Enhet!!Motsvarighet i kPa!!Motsvarighet i bar!!Motsvarighet i PSI!!Motsvarighet i mmHg!!Motsvarighet i mmVp!!Motsvarighet i mVp!!Motsvarighet i atm
|-
|'''bar'''||100||1||14,5||750,06||10190||10,19||0,99
|-
|'''PSI'''||6,89||0,069||1||51,71||703||0,70||0,068
|-
|'''mmHg'''||0,13||0,0013||0,019||1||13,59||0,01359||0,0013
|-
|'''mmVp'''||0,0098||98·10<sup>−6</sup>||0,0014||0,074||1||0,001||97·10<sup>−6</sup>
|-
|'''mVp'''||9,81||0,098||1,42||73,56||1000||1||0,097
|-
|'''atm'''||101,325||1,01325||14,70||760||10 330||10,33||1
|}
<br>
<br>
<br>
<br>
Rad 84: Rad 66:


== Tryck i vätskor och gaser ==
== Tryck i vätskor och gaser ==
[[File:ALVIN submersible.jpg|thumb|ALVIN submersible]]
[[File:ALVIN submersible.jpg|thumb|ALVIN submersible]]
{{heureka|Läs härledningen boken sidan 49.}}
=== Experiment: Brusraketen ===


to v 8
[http://school.chem.umu.se/Experiment/59 Brusraketen]


'''En tillbakablick'''
=== En tillbakablick ===


[http://www.geogebratube.org/student/m2340 GGB med mätvärden och derivator]
[http://www.geogebratube.org/student/m2340 GGB med mätvärden och derivator]


'''Tryck i vätskor'''
=== Tryck i vätskor ===


  p = ρ g h  (Pascals lag)
  p = ρ g h  (Pascals lag)


'''Sir Richard Branson'''
==== Härledning av Pascals lag ====
 
: F = mg
: p = m/V <==> m = Vp
: p = F/A
 
tänk dig en area på djupet h
 
: p = F/A = mg/A = Vpg/A = hpg
 
==== Räkna själv ====
 
{{uppgruta|'''Döda havet'''
Döda havet är 65 kilometer långt, upp till 18 kilometer brett och det största djupet är 378 meter. Vattnet har en salthalt på omkring 33,7 procent vilket ger saltvattnet en densitet på 1.24 g/cm<sup>3</sup>.
 
{{enwp|Dead_Sea}}
 
'''Beräkna''' vattentrycket på den djupaste platsen.
}}
<br />
 
=== Sir Richard Branson ===


Kolla filmerna och besvara frågorna:
Kolla filmerna och besvara frågorna:
Rad 104: Rad 111:
Gör ett antagande för glasets yta och räkna ut vilken kraft det måste tåla
Gör ett antagande för glasets yta och räkna ut vilken kraft det måste tåla


<youtube>_Sk_XEHfqwk</youtube><youtube>FB9aB8LwHws</youtube>
{{#ev:youtube|_Sk_XEHfqwk|240|left}}


[http://en.wikipedia.org/wiki/Siphon Häverten (Wikipedia)]
[http://en.wikipedia.org/wiki/Siphon Häverten (Wikipedia)]
{{clear}}


'''Hydrostatiska paradoxen'''
=== Hydrostatiska paradoxen ===


  Trycket på botten av ett kärl beror bara på djupet inte på formen.
  Trycket på botten av ett kärl beror bara på djupet inte på formen.
  Med djupet menas avståndet upp till vattenytan.
  Med djupet menas avståndet upp till vattenytan.
<br />
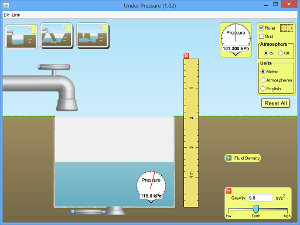
<html>
<div style="position: relative; width: 300px; height: 226px;"><a href="http://phet.colorado.edu/sims/fluid-pressure-and-flow/under-pressure_en.jnlp" style="text-decoration: none;"><img src="http://phet.colorado.edu/sims/fluid-pressure-and-flow/under-pressure-screenshot.png" alt="Under Pressure" style="border: none;" width="300" height="226"/><div style="position: absolute; width: 200px; height: 80px; left: 50px; top: 73px; background-color: #FFF; opacity: 0.6; filter: alpha(opacity = 60);"></div><table style="position: absolute; width: 200px; height: 80px; left: 50px; top: 73px;"><tr><td style="text-align: center; color: #000; font-size: 24px; font-family: Arial,sans-serif;">Click to Run</td></tr></table></a></div>
</html>
<br />
{{clear}}


'''Pascals princip - kraftförstärkning'''
=== Pascals princip - kraftförstärkning ===


  Trycket i någon del av vätskan överförs till alla delar av vätskan.
  Trycket i någon del av vätskan överförs till alla delar av vätskan.
Rad 123: Rad 137:
[[Fil:Principe_de_Pascal.jpg|right|CC [http://upload.wikimedia.org/wikipedia/commons/f/f1/Principe_de_Pascal.jpg?uselang=sv By]]]
[[Fil:Principe_de_Pascal.jpg|right|CC [http://upload.wikimedia.org/wikipedia/commons/f/f1/Principe_de_Pascal.jpg?uselang=sv By]]]


<youtube>A3ormYVZMXE</youtube><youtube>TL3DcMZQEog</youtube>
{{#ev:youtube|A3ormYVZMXE |240|left}}


Den övre/vänstra filmen innehåller ett fel, vilket? Den högtra är bra men använcder ovanliga enheter. Var används dessa?
Den övre/vänstra filmen innehåller ett fel, vilket? Den högtra är bra men använcder ovanliga enheter. Var används dessa?


'''Evighetsmaskiner finns inte eller hur...'''
=== Evighetsmaskiner finns inte eller hur... ===


[http://physics.stackexchange.com/questions/8784/troll-physics-buoyancy-for-infinite-power Troll Physics]
[http://physics.stackexchange.com/questions/8784/troll-physics-buoyancy-for-infinite-power Troll Physics]
Rad 145: Rad 159:
{{clear}}
{{clear}}


== Archimeds princip, s 112-114 ==
== Lufttryck ==
[[Fil:Domenico-Fetti Archimedes 1620.jpg|miniatyr|Arkimedes på en målning av Domenico Fetti, 1620. ]]
 
Arkimedes princip beskriver den kraft som påverkar ett föremål vilket sänks ned i en vätska. Den säger att "ett föremål nedsänkt i vätska påverkas av en uppåtriktad kraft, som är lika stor som tyngden av den undanträngda vätskan". Lyftkraftens storlek F är alltså proportionell mot volymen V av den del av föremålet som är nedsänkt i vätskan genom sambandet F = ρ V g, där ρ är vätskans densitet och ρV därmed den undanträngda massan medan g är jordens tyngdacceleration. Principen upptäcktes av Arkimedes.
 
Om föremålet har lägre densitet än vätskan, blir lyftkraften så stor att föremålet flyter. Har det större densitet än vätskan, till exempel järn i vatten, kan det fås att flyta om formen anpassas så att föremålet exempelvis förvarar luft under omgärdande vätskeyta. I detta fall blir densiteten av "föremålet", som tränger undan vätskan, ett medelvärde av järnets och luftens; medeldensiteten för föremålet blir lägre än vätskans densitet.
 
Observera dock att Arkimedes princip gäller även i andra media än vätskor. Sålunda påverkas varje föremål som befinner sig i luft av en lyftkraft, om än liten. Också här gäller regeln att ju större föremålets volym är, desto större är lyftkraften. Därför har i en normal situation en klump bly en (marginellt) större tyngd än en mängd bomull med samma massa.
''[http://sv.wikipedia.org/wiki/Arkimedes_princip Texten ovan från Wikipedia]''
 
=== Demo: Fingret i vattenglaset ===
 
Man skulle kunna ha vågar med vattenglas på som eleverna får komma fram till och pröva. Sedan får de skriva sin förklaring (i datorn och publicera?).
 
* [http://www.thenakedscientists.com/HTML/content/kitchenscience/exp/weighing-buoyancy/ Kitchen Science Experiments]
* [http://www.danielbarker.se/fysik-a/akrimedes-princip Daniel Barker]
 
'''Lösingar:''' [[Media:B-07122011122533.pdf|Lösningar till uppgift 614-620]]
 
== Lufttryck, s114-117 ==
[[Fil:442px-NSRW_Torricelli's_experiment.jpg|thumb|CC http://commons.wikimedia.org/wiki/File:NSRW_Torricelli%27s_experiment.jpg|Torricelli tog ett två meter långt glasrör som han fyllde med kvicksilver och vände upp och ner i en skål. Det bildades en 76 cm hög pelare av kvicksilver i röreet. Det är lufttrycket som trycker upp kvicksilvret. CC Wikipedia.]]
[[Fil:442px-NSRW_Torricelli's_experiment.jpg|thumb|CC http://commons.wikimedia.org/wiki/File:NSRW_Torricelli%27s_experiment.jpg|Torricelli tog ett två meter långt glasrör som han fyllde med kvicksilver och vände upp och ner i en skål. Det bildades en 76 cm hög pelare av kvicksilver i röreet. Det är lufttrycket som trycker upp kvicksilvret. CC Wikipedia.]]
{{heureka|Läs i boken sidan 55-56.}}


På 1600-talet försökte man pumpa vatten ur gruvor. Man märkte att man bara kunde pumpa 10 m högt.
På 1600-talet försökte man pumpa vatten ur gruvor. Man märkte att man bara kunde pumpa 10 m högt.
Rad 174: Rad 170:


'''Totala trycket i en vätska'''
'''Totala trycket i en vätska'''
Totala trycket i en vätska är summan av lufttrycket och vätsketrycket.
   
   
  p = p<sub>0</sub> + ρ g h
  p = p<sub>0</sub> + ρ g h
Rad 182: Rad 180:
  h är djupet i vätskan
  h är djupet i vätskan


<br>
[[Image:aneroid barometer.JPG|300px|left|En gammal aneroidbarometer]]
<youtube>jzjQqtGFifs</youtube>
[[Fil:Aneroidbarometer.png|300px|right|Ritning av aneroidbarometer.]]
<youtube>vR5tXurNlsM</youtube>
 
<br>
Det förekommer två typer av barometrar:
 
# '''aneroidbarometer''' som mäter det absoluta trycket, till exempel lufttrycket i relation till vakuum.
# '''manometern''' som mäter en tryckskillnad mellan två utrymmen, till exempel övertrycket i ett pumpat bildäck.
<br />
[http://sv.wikipedia.org/wiki/Kvicksilverbarometer Läs om barometern].
[http://sv.wikipedia.org/wiki/Kvicksilverbarometer Läs om barometern].
{{clear}}


{{#ev:youtube|jzjQqtGFifs|240|left}}
{{#ev:youtube|vR5tXurNlsM|240|right}}
Detta är två filmer som visar på kul effekter av undertryck.
<br />
{{clear}}
Lösningar: [[Media:C-07122011122610.pdf|Lösningar till uppgift 621-625]]
Lösningar: [[Media:C-07122011122610.pdf|Lösningar till uppgift 621-625]]


== Ideala gaslagen, s 118-120 ==
{{uppgruta|'''Vattentryck och lufttryck'''
to v11


=== Allmänna gaslagen ===
PÅ vilket djup är vattentrycket lika stort som lufttrycket vid vattenytan?
 
pV = nRT
Lufttrycket vid vattenytan är 101.3 kPa.
}}
där p = trycket, V är volymen, T = temperaturen,
n är antalet partiklar i gasen och R är allmänna gaslagen.
R = 8.314 J/(mol*Kelvin)


=== Simuleringar ===
{{Läxa|Ni får en ganska tuff läxa.
:Läs sidorna 44-56.
}}
{{clear}}


Här är två olika simuleringar av gaser i behållare:
=== Förnöjande film ===
<br>
<br>
<youtube>2VHneRg0mhI</youtube>
<br>
<br>
<html><div style="position: left; width: 300px; height: 228px;"><a href="http://phet.colorado.edu/sims/ideal-gas/gas-properties_en.jnlp" style="text-decoration: none;"><img src="http://phet.colorado.edu/sims/ideal-gas/gas-properties-screenshot.png" alt="Gas Properties" style="border: none;" width="300" height="228"/><div style="position: absolute; width: 200px; height: 80px; left: 50px; top: 74px; background-color: #FFF; opacity: 0.6; filter: alpha(opacity = 60);"></div><table style="position: absolute; width: 200px; height: 80px; left: 50px; top: 74px;"><tr><td style="text-align: center; color: #000; font-size: 24px; font-family: Arial,sans-serif;">Click to Run</td></tr></table></a></div></html>


<html><div style="position: right; width: 300px; height: 225px;"><a href="http://phet.colorado.edu/sims/states-of-matter/states-of-matter_en.jnlp" style="text-decoration: none;"><img src="http://phet.colorado.edu/sims/states-of-matter/states-of-matter-screenshot.png" alt="States of Matter" style="border: none;" width="300" height="225"/><div style="position: absolute; width: 200px; height: 80px; left: 50px; top: 72px; background-color: #FFF; opacity: 0.6; filter: alpha(opacity = 60);"></div><table style="position: absolute; width: 200px; height: 80px; left: 50px; top: 72px;"><tr><td style="text-align: center; color: #000; font-size: 24px; font-family: Arial,sans-serif;">Click to Run</td></tr></table></a></div></html>
== Archimeds princip, s 112-114 ==
<br>
[[Fil:Domenico-Fetti Archimedes 1620.jpg|miniatyr|Arkimedes på en målning av Domenico Fetti, 1620. ]]
<br>
 
Arkimedes princip beskriver den kraft som påverkar ett föremål vilket sänks ned i en vätska. Den säger att "ett föremål nedsänkt i vätska påverkas av en uppåtriktad kraft, som är lika stor som tyngden av den undanträngda vätskan". Lyftkraftens storlek F är alltså proportionell mot volymen V av den del av föremålet som är nedsänkt i vätskan genom sambandet F = ρ V g, där ρ är vätskans densitet och ρV därmed den undanträngda massan medan g är jordens tyngdacceleration. Principen upptäcktes av Arkimedes.
 
Om föremålet har lägre densitet än vätskan, blir lyftkraften så stor att föremålet flyter. Har det större densitet än vätskan, till exempel järn i vatten, kan det fås att flyta om formen anpassas så att föremålet exempelvis förvarar luft under omgärdande vätskeyta. I detta fall blir densiteten av "föremålet", som tränger undan vätskan, ett medelvärde av järnets och luftens; medeldensiteten för föremålet blir lägre än vätskans densitet.


=== En klurig film ===
Observera dock att Arkimedes princip gäller även i andra media än vätskor. Sålunda påverkas varje föremål som befinner sig i luft av en lyftkraft, om än liten. Också här gäller regeln att ju större föremålets volym är, desto större är lyftkraften. Därför har i en normal situation en klump bly en (marginellt) större tyngd än en mängd bomull med samma massa.
''[http://sv.wikipedia.org/wiki/Arkimedes_princip Texten ovan från Wikipedia]''


Nu är vi klara med detta kapitel och har alla verktygen för att förklara vardagliga fenomen exempelvis det i filmen nedan:
{{#ev:youtube|rMwp-ztn9sg}}


<youtube>j2k40Hw3GI0</youtube>
'''Arkimedes princip'''


=== Laboration på gång ===
ett föremål nedsänkt i vätska påverkas av en uppåtriktad kraft,
som är lika stor som tyngden av den undanträngda vätskan
F = ρ V g,
där F är lyftkraftens storlek, ρ är vätskans densitet, V är volymen och g är jordens tyngdacceleration.


Dela ut labbinstruktion till Arkimedeslabb.
=== Demo: Fingret i vattenglaset ===


=== Länkar: Ideala gaslagen ===
Man skulle kunna ha vågar med vattenglas på som eleverna får komma fram till och pröva. Sedan får de skriva sin förklaring (i datorn och publicera?).


http://sv.wikipedia.org/wiki/Ideala_gaslagen
* [http://www.thenakedscientists.com/HTML/content/kitchenscience/exp/weighing-buoyancy/ Kitchen Science Experiments]


http://sv.wikipedia.org/wiki/Boyles_lag
'''Lösingar till Nexus A:''' [[Media:B-07122011122533.pdf|Lösningar till uppgift 614-620]]
<br />


== Diagnostiskt test ==
{{Uppgruta|'''En vätskas lyftkraft'''
[[Fil:Silja Serenade.jpg|thumb]]
Silja Serenade färdas mot Stockholm med 22 knop. Hon är känd för sin 140 m långa gågata. Silja Serenade väger cirka 5 500 ton. Hon har 13 däcksplan och hon tar 2852 passagerare. 
# Hur stor är vattnets lyftkraft på båten?
# Hur stor volym vatten tränger hennes skrov undan?
}}


måndag v11
{{exruta|'''Lyftkraften i en gas'''
{{#ev:youtube|rsPoSoy5vAE|240|right}}
Arikemedes princip gäller även för gaser och bebisar.


Diagnostestet tar cirka 40 min. Här finns [[facit till tryckdiagnosen]].
Alice i filmen till höger suger i sig heliumgasen för att prata om ditt och datt på Youtube. Om hon istället hade sparat sina ballonger hade hon kunnat ta en flygtur. Hur många liter gas hade hon behövt spara för att kunna lätta från marken?
}}
<br />


Därefter finns tid för att räkna uppgifter ur boken.
{{uppgruta| '''Arkimedes och guldkronan'''


== Laboration - Arkimedes ==
[[File:Archimedes water balance.gif|thumb|right|Archimedes water balance]]


Torsdag v11
Förklara vad som händer i fallet med Arkimedes och guldkronan


Före vi labbar går vi igenom diagnosen helt kort, cirka 10 min.
{{enwp|Archimedes}}


Vi labbar i helklass. läs på instruktionen i förväg.
Detta är en lämplig uppgift som avslutning av en lektion. Låt gärna eleverna skriva sina förklaring på lappar som samlas in eller [http://todaysmeet.com/Guldkronan TodaysMeet].
}}


=== Didaktisk kommentar till laborationen ===
== Ett gammalt diagnostiskt test med lösningar ==


Skulle man inte kunna plocka ut sista delen med träklossen och vannan och göra den som en demo i helklass med klassrumsdiskussion. Den följer nämligen inte tankespåret i de övriga momenten i labben.
Själva testet finns inte fritt men här är en kopia med lösningar: [[facit till tryckdiagnosen]].


== Repetition ==
== Repetition ==


Låt oss först konstatera att det här är ett relativt lätt prov. Det rör sig om ett kapitel. Och ett ganska kort ett dessutom. Femton sidor och tre formeler....
Låt oss först konstatera att det här är ett relativt lätt prov. Det rör sig om kapitel 1-3.Få sidor och fem formeler....
 
=== Skapa malluppgifter åt varandra ===
 
{{uppgruta| '''Malldokumentet för fysikuppgifter'''
 
Problemlösning med hjälp av malldokument:
 
Du får en av uppgifterna; 3.6, 3.10, 3.13, 2.25, 3.27, 3.28.
 
Ni löser olika uppgifter. Sedan jämför vi lösningarna och fotar den bästa som sedan visas från IPad till projektor och diskuteras.
 
Vi lägger ihpop de lösta uppgifterna i en pdf.
 
Därefter får ni ett kompendium med uppgifter att öva på hemma.
}}
 
=== Övningsuppgifter ===


=== Pluggtips ===
{{TIS| Åke Dahlöf |


* Börja med att läsa sammanfattningen på sidan 121 så att du får en känsla för vad du behöver lära dig mer om.
: [[media:Övning_i_densitet.pdf|Exempel: Övning i densitet]]
* Du bör läsa sidorna 105-120.
:  [[media:Övningsuppgifter_på_densitet.pdf|Övningsuppgifter på densitet]]
* Titta gärna igenom denna sida på wikiskola.se
: [[media:Övningsblad_på_Archimedes_Princip.pdf| Övningsblad Arkimedes proincip]]
* Exemplen: 6.1-6.8 är alla lämpliga att studera noggrant. Här ser du exakt hur du kan ställa upp dina lösningar.
: [[Media:Extra_övningsblad_Arkimedes_princip.pdf| Extra övningsblad Arkimedes princip]]
* Räkna många av de blandade uppgifterna på sidorna 122-123.
}}


=== Läsanvisningar ===
{{tnkruta | '''Kluring'''


* Sid 105 är ger dig formeln för tryck mellan fasta kroppar och dessutom omvandling mellan enheter.
Vad blir lyftkraften om man sänker ner universum i vatten?
* Vätsktryck på sid 107 är viktigt.
}}
* Läs om den hydrostatiska paradoxen och Pascals princip så att du har det med dig för kommande resonemang.
* På sidan 112 bör du läsa '''noga''' om Archimedes princip även om du inte behöver kunna göra härledningen själv.
* Du läser om lufttryck på sid 114-115 för att förstå hur formeln ska användas.
* Läs texterna på sid 116-117 som allmänbildning i fysik.
* Allmänna gaslagen på sid 118 är betydelsefull, speciellt som den tillämpas i Exempel 6.7.
* Läs sidan 127 för att det är kul att veta mer om dinosaurierna.


=== Övningsprov ===
=== Övningsprov ===


Öva på ett [http://lararwebb.orebro.se/lasam23/NV1/FY/prov_VT10_tryck_version2_facit.pdf gammalt prov från Örebro], Med lösningar.
Vi delar ut ett [[övningsprov med G-uppgifter om Tryck]].
 
Facit till [[Prov: Tryck version 1 med lösningar | Prov: Tryck version 1 med handskrivna lösningar]]
 
=== Elevaktiv formativ bedömning ===


Vi delar ut ett [[övningsprov med G-uppgifter om Tryck]].
Prov kap 1-3 ver 2.2


Facit till [[Prov: Tryck version 1 med lösningar]]
Två rättningsmallar som är nästan kompletta:
: [[media:Prov_Fysik_1_kap_1-3_krafter_tryck_och_densitet_version_2_2_-_Bedomningsmall.pdf|Rättningsmall baserad på elevernas lösningar]]
: [[Media:Prov,_Fysik_1_kap_1-3_krafter_tryck_och_densitet_Mattias_R_mall.pdf| Mattias rättningsmall till Prov version 2.2]]


=== Förnöjande film ===
==== Powerpoint till uppgiften om universums denitet ====
<br>
<youtube>2VHneRg0mhI</youtube>
<youtube>ntjHVQOKDdo</youtube>
<br>


== Prov - Torsdag v 12 ==
{{PPT| [[Media:Universums_densitet_lösningsexempel.ppt | Universums densitet ]]}}

Nuvarande version från 25 oktober 2017 kl. 14.15

Konvertera till SI-enheter

Som i all fysik är det nödvändigt att göra om de värden du får till SI-enheter innan du sätter in dem i formler och gör beräkningar. När du arbetar med tryck är det extra viktigt.

Antag att du behöver konvertera 24 dm3 till m3. Hur gör du då?

Det är enkelt om du använder Wolfram Alpha. Skriv till exempel 1 dm^3 i inmatningsrutan så får du se.

Eller pröva att göra om 740 mmHg till bar.

Densitet

Formeln för densiteten är: 

ρ = m / V

där ρ är densiteten,  m är massan och V är volymen

Densitetstabell

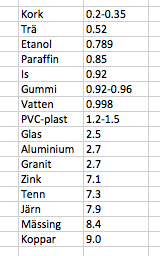
En liten densitets-tabell med riktiga värden?

Fullständig tabell över grundämnenas densitet finns här: Wikipedia:Densities_of_the_elements_(data_page)

Tänk på att SI-enheten för densitet är kg/m3

1 g/cm3 = 1000 kg/m3

Uppgift

Uppgift
Beräkna massan

Kolla i formelsamlingen. Hitta grundämnet med högst densitet.

Hur mycket väger ett klot med radien 2 cm av det ämnet?


Uppgift
Flyter is på olja?

Testa hemma.

Läs på hos ResursCentrum för Kemi


Tryck mellan fasta kroppar, sid 105-106

p = F / A
 
där p är trycket i N/m2 = pascal, Pa
F är kraften, ofta mg. Kraften anges i Newton, N.
A är arean i m2

Tryckenheter

Omvandling av tryckenheter

Tabellen kommer från Wikipedia.

Omvandlingstabell för tryckenheter
Enhet Motsvarighet i kPa Motsvarighet i bar Motsvarighet i PSI Motsvarighet i mmHg Motsvarighet i mmVp Motsvarighet i mVp Motsvarighet i atm
bar 100 1 14,5 750,06 10190 10,19 0,99
PSI 6,89 0,069 1 51,71 703 0,70 0,068
mmHg 0,13 0,0013 0,019 1 13,59 0,01359 0,0013
mmVp 0,0098 98·10−6 0,0014 0,074 1 0,001 97·10−6
mVp 9,81 0,098 1,42 73,56 1000 1 0,097
atm 101,325 1,01325 14,70 760 10 330 10,33 1





Räkna 601-607

Tryck i vätskor och gaser

ALVIN submersible

NoK Heureka Fysik 1: Läs härledningen boken sidan 49.


Experiment: Brusraketen

Brusraketen

En tillbakablick

GGB med mätvärden och derivator

Tryck i vätskor

p = ρ g h  (Pascals lag)

Härledning av Pascals lag

F = mg
p = m/V <==> m = Vp
p = F/A

tänk dig en area på djupet h

p = F/A = mg/A = Vpg/A = hpg

Räkna själv

Uppgift
Döda havet

Döda havet är 65 kilometer långt, upp till 18 kilometer brett och det största djupet är 378 meter. Vattnet har en salthalt på omkring 33,7 procent vilket ger saltvattnet en densitet på 1.24 g/cm3.

Wikipedia:Dead_Sea

Beräkna vattentrycket på den djupaste platsen.


Sir Richard Branson

Kolla filmerna och besvara frågorna:

Hur djupt kan undervattensfarkosten gå? Vilket är trycket där? Gör ett antagande för glasets yta och räkna ut vilken kraft det måste tåla

Load video
YouTube

Häverten (Wikipedia)

Hydrostatiska paradoxen

Trycket på botten av ett kärl beror bara på djupet inte på formen.
Med djupet menas avståndet upp till vattenytan.


Under Pressure
Click to Run


Pascals princip - kraftförstärkning

Trycket i någon del av vätskan överförs till alla delar av vätskan.

(P1) = (P2)

(F1)/(A1) = (F2)/(A2)
CC By
CC By
Load video
YouTube

Den övre/vänstra filmen innehåller ett fel, vilket? Den högtra är bra men använcder ovanliga enheter. Var används dessa?

Evighetsmaskiner finns inte eller hur...

Troll Physics

Lösningar: Lösningar till uppgifterna 608-613

Diskussionsuppgift

Hydraylic disc brake diagram

Figuren visar ett bromssystem men en pistong (1) vid bromspedalen och en pistong (2) vid bromsskivan. Pistong 1 är grövre än tvåan. Vilka av följande påstående stämmer?

  1. p1 = P2
  2. A1 = A2
  3. F p1 = F2
  4. Det här systemet fungerar som en hävarm och visar mekanikens gyllene regel. Det man vinner i kraft förlorar man i väg.
  5. Detta är Pascals princip.

Lufttryck

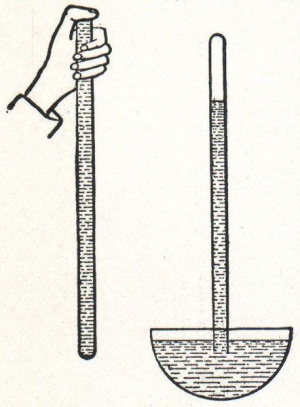
Torricelli tog ett två meter långt glasrör som han fyllde med kvicksilver och vände upp och ner i en skål. Det bildades en 76 cm hög pelare av kvicksilver i röreet. Det är lufttrycket som trycker upp kvicksilvret. CC Wikipedia.

NoK Heureka Fysik 1: Läs i boken sidan 55-56.


På 1600-talet försökte man pumpa vatten ur gruvor. Man märkte att man bara kunde pumpa 10 m högt.

Normalt tryck vid havsytan 

p0 = 101.3 kPa

Totala trycket i en vätska

Totala trycket i en vätska är summan av lufttrycket och vätsketrycket. 

p = p0 + ρ g h

där p0 är lufttrycket mot vätskeytan
ρ är vätskans densitet
g är tyngdaccelerationen
h är djupet i vätskan
En gammal aneroidbarometer
En gammal aneroidbarometer
Ritning av aneroidbarometer.
Ritning av aneroidbarometer.

Det förekommer två typer av barometrar:

  1. aneroidbarometer som mäter det absoluta trycket, till exempel lufttrycket i relation till vakuum.
  2. manometern som mäter en tryckskillnad mellan två utrymmen, till exempel övertrycket i ett pumpat bildäck.


Läs om barometern.

Load video
YouTube
Load video
YouTube

Detta är två filmer som visar på kul effekter av undertryck.

Lösningar: Lösningar till uppgift 621-625

Uppgift
Vattentryck och lufttryck

PÅ vilket djup är vattentrycket lika stort som lufttrycket vid vattenytan?

Lufttrycket vid vattenytan är 101.3 kPa.


Läxa! Ni får en ganska tuff läxa.

Läs sidorna 44-56.

Förnöjande film


Load video
YouTube


Archimeds princip, s 112-114

Arkimedes på en målning av Domenico Fetti, 1620.

Arkimedes princip beskriver den kraft som påverkar ett föremål vilket sänks ned i en vätska. Den säger att "ett föremål nedsänkt i vätska påverkas av en uppåtriktad kraft, som är lika stor som tyngden av den undanträngda vätskan". Lyftkraftens storlek F är alltså proportionell mot volymen V av den del av föremålet som är nedsänkt i vätskan genom sambandet F = ρ V g, där ρ är vätskans densitet och ρV därmed den undanträngda massan medan g är jordens tyngdacceleration. Principen upptäcktes av Arkimedes.

Om föremålet har lägre densitet än vätskan, blir lyftkraften så stor att föremålet flyter. Har det större densitet än vätskan, till exempel järn i vatten, kan det fås att flyta om formen anpassas så att föremålet exempelvis förvarar luft under omgärdande vätskeyta. I detta fall blir densiteten av "föremålet", som tränger undan vätskan, ett medelvärde av järnets och luftens; medeldensiteten för föremålet blir lägre än vätskans densitet.

Observera dock att Arkimedes princip gäller även i andra media än vätskor. Sålunda påverkas varje föremål som befinner sig i luft av en lyftkraft, om än liten. Också här gäller regeln att ju större föremålets volym är, desto större är lyftkraften. Därför har i en normal situation en klump bly en (marginellt) större tyngd än en mängd bomull med samma massa. Texten ovan från Wikipedia

Load video
YouTube

Arkimedes princip 

ett föremål nedsänkt i vätska påverkas av en uppåtriktad kraft, 
som är lika stor som tyngden av den undanträngda vätskan

F = ρ V g, 

där F är lyftkraftens storlek, ρ är vätskans densitet, V är volymen och g är jordens tyngdacceleration.

Demo: Fingret i vattenglaset

Man skulle kunna ha vågar med vattenglas på som eleverna får komma fram till och pröva. Sedan får de skriva sin förklaring (i datorn och publicera?).

Lösingar till Nexus A: Lösningar till uppgift 614-620

Uppgift
En vätskas lyftkraft

Silja Serenade färdas mot Stockholm med 22 knop. Hon är känd för sin 140 m långa gågata. Silja Serenade väger cirka 5 500 ton. Hon har 13 däcksplan och hon tar 2852 passagerare.

  1. Hur stor är vattnets lyftkraft på båten?
  2. Hur stor volym vatten tränger hennes skrov undan?


Exempel
Lyftkraften i en gas
Load video
YouTube

Arikemedes princip gäller även för gaser och bebisar.

Alice i filmen till höger suger i sig heliumgasen för att prata om ditt och datt på Youtube. Om hon istället hade sparat sina ballonger hade hon kunnat ta en flygtur. Hur många liter gas hade hon behövt spara för att kunna lätta från marken?


Uppgift
Arkimedes och guldkronan
Archimedes water balance

Förklara vad som händer i fallet med Arkimedes och guldkronan

Wikipedia:Archimedes

Detta är en lämplig uppgift som avslutning av en lektion. Låt gärna eleverna skriva sina förklaring på lappar som samlas in eller TodaysMeet.


Ett gammalt diagnostiskt test med lösningar

Själva testet finns inte fritt men här är en kopia med lösningar: facit till tryckdiagnosen.

Repetition

Låt oss först konstatera att det här är ett relativt lätt prov. Det rör sig om kapitel 1-3.Få sidor och fem formeler....

Skapa malluppgifter åt varandra

Uppgift
Malldokumentet för fysikuppgifter

Problemlösning med hjälp av malldokument:

Du får en av uppgifterna; 3.6, 3.10, 3.13, 2.25, 3.27, 3.28.

Ni löser olika uppgifter. Sedan jämför vi lösningarna och fotar den bästa som sedan visas från IPad till projektor och diskuteras.

Vi lägger ihpop de lösta uppgifterna i en pdf.

Därefter får ni ett kompendium med uppgifter att öva på hemma.


Övningsuppgifter

Åke Dahlöf har skapat och delar

Exempel: Övning i densitet
Övningsuppgifter på densitet
Övningsblad Arkimedes proincip
Extra övningsblad Arkimedes princip


Tänk! Kluring

Vad blir lyftkraften om man sänker ner universum i vatten?


Övningsprov

Vi delar ut ett övningsprov med G-uppgifter om Tryck.

Facit till Prov: Tryck version 1 med handskrivna lösningar

Elevaktiv formativ bedömning

Prov kap 1-3 ver 2.2

Två rättningsmallar som är nästan kompletta:

Rättningsmall baserad på elevernas lösningar
Mattias rättningsmall till Prov version 2.2

Powerpoint till uppgiften om universums denitet

Se en PowwerPoint! Universums densitet

Hämtad från ”https://wikiskola.se/index.php?title=Densitet_och_Tryck_Fysik1&oldid=42045”