(22 mellanliggande sidversioner av samma användare visas inte)
Rad 1:
Rad 1:
== Uppgifter för år sex ungefär ==
== Kängurutävlingar ==
Det är nödvändigt att öva problemlösning regelbundet. Man kan ta en del av en gammal tävling och köra som avslutning av en lektion. Sedan fortsätter man en annan lektion. Tävlingstiden är 60 minuter så på tre gånger 20 min bör alla ha hunnit med det emsta. Sedan rättar vi gemensamt och går igenom lösningar tillsammans.
Jag väljer att kopiera upp proven för att inte haka uppsig i procedurer med datorn och för att papper och penna begränsar tanken mindre.
*Ht 2008 gjorde jag benjamin 2008 med mina sexor och sjuor.
*februari-mars gjorde jag [http://ncm.gu.se/media/namnaren/kanguru/2007/webb/benjamin07.pdf Benjamin 2007] med mina sexor och sjuor.
== Uppgifter för år sju ungefär ==
== Metoder ==
#Hur många fotbollar finns det i skåpet, frågar Håkan? Det är sex stycken plus två tredjedelar av alla fotbollar i skåpet.
Paul Vaderlind besökte mina klasser en lektion våren 2006. Jag skrev rent mina [http://manotek.se/problemlosning/paul_vaderlind.doc antectkningar] och lade in frågor till eleverna för att de ska kunna tänka igenom problemen i lugn och ro.
#Skriv talen 1, 2, 3, .. , 10 med hjälp av fyra fyror och de vanliga räknesätten.
Exempelvis är 1 = 4/4 + 4 - 4
== Rita en bild ==
#x
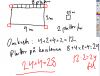
* [[Fil:Problemlösningnr12.png|left|100px]][[Fil:Problemlosning_ar6_vt_nr12.png|100px|right]]. Lösing till Problemlösning uppgift 12 i MD år 6B (vt)
Lösning till uppgift 16 i MD6B Problemlösning kap 10.
[[Fil:Problemlösnignr16.png|left|100px]]
Det är krångligt med köer. Man kan inte bara räkan tere plus fem.
För personen i mitten ska ju inte räknas två gånger.
== Pröva ==
[[Fil:Problemlösningnr21.png|right|100px]]
upgiften handlar om ....
här gäller et att pröva sig fram
Gissa på en ålder på Quang. Räkna ut pappans ålder. Räkna ut vad som händer efter fem år. Kolla om det stämmer.
Testa nya värden tills det stämmer.
== Antaganden ==
Det är viktigt att eleverna övar sig i att göra riktiga [http://manotek.se/ma_antaganden/Index_ma_antaganden.htm antaganden]. De bör inte få alla värden serverade. Jag har några introducerande uppgifter på detta. Ytterligare en uppgift som kräver att man gör en del antaganden är:
*[[Matematiken bakom öresauktioner]]
Det finns flera bra metoder att ta till vid problemlösning, exempelvis att pröva, rita bilder, göra tabeller, osv. Denna [[Media:Problemlosning.ppt|powerpoint om problemlösning]] visar några exempel.
== Blandade uppgifter ==
Här finns några [http://manotek.se/problemlosning/profildag.doc uppgifter] till profildagen.
[http://manotek.se/problemlosning/egna_problemuppgifter.html Några av mina egna uppgifter]
[[Ett projekt om problemlösnning för år sex till sju ungefär]]
== Hemuppgifter av problemlösningskaraktär. ==
Jag använde dessa i en åtta och tyckte att det räckte bra med en uppgift per veckaeftersom lösningarna kan bli relativt omfattande. Det hände ofta att eleverna diskuterade uppgifterna på rasterna:<br />[http://manotek.se/problemlosning/Hemuppgift_1_Utspilld_mjolk.doc Hemuppgift 1] om utspilld mjölk<br />[http://manotek.se/problemlosning/Hemuppgift_4_fabrikorerna.doc Hemuppgift 4] - Fabrikörerna<br />[http://manotek.se/problemlosning/Hemuppgift_5_Den_optiska_telegrafen.doc Hemuppgift 5] – Den optiska telegrafen<br />[http://manotek.se/problemlosning/Hemuppgift_6_Mattband_for_spagetti.doc Hemuppgift 6] – Spagettimåttet - med [http://manotek.se/problemlosning/hemuppgift_6_ Mattband_for_spagetti_losning.ppt lösningsförslag].<br />[http://manotek.se/problemlosning/Hemuppgift_7_Fjarilen_i_glaskupan.doc Hemuppgift 7] – Fjärilen i glaskupan <br />[http://manotek.se/problemlosning/Hemuppgift_11_stora_tal_i_datorns_varld.doc Hemuppgift 11] – Stora tal i datorns värld - med [http://manotek.se/problemlosning/Hemuppgift_11_losningar.doc lösningsförslag].
Det är nödvändigt att öva problemlösning regelbundet. Man kan ta en del av en gammal tävling och köra som avslutning av en lektion. Sedan fortsätter man en annan lektion. Tävlingstiden är 60 minuter så på tre gånger 20 min bör alla ha hunnit med det emsta. Sedan rättar vi gemensamt och går igenom lösningar tillsammans.
Jag väljer att kopiera upp proven för att inte haka uppsig i procedurer med datorn och för att papper och penna begränsar tanken mindre.
Ht 2008 gjorde jag benjamin 2008 med mina sexor och sjuor.
februari-mars gjorde jag Benjamin 2007 med mina sexor och sjuor.
Metoder
Paul Vaderlind besökte mina klasser en lektion våren 2006. Jag skrev rent mina antectkningar och lade in frågor till eleverna för att de ska kunna tänka igenom problemen i lugn och ro.
Rita en bild
. Lösing till Problemlösning uppgift 12 i MD år 6B (vt)
Lösning till uppgift 16 i MD6B Problemlösning kap 10.
Det är krångligt med köer. Man kan inte bara räkan tere plus fem.
För personen i mitten ska ju inte räknas två gånger.
Pröva
upgiften handlar om ....
här gäller et att pröva sig fram
Gissa på en ålder på Quang. Räkna ut pappans ålder. Räkna ut vad som händer efter fem år. Kolla om det stämmer.
Testa nya värden tills det stämmer.
Antaganden
Det är viktigt att eleverna övar sig i att göra riktiga antaganden. De bör inte få alla värden serverade. Jag har några introducerande uppgifter på detta. Ytterligare en uppgift som kräver att man gör en del antaganden är:
Det finns flera bra metoder att ta till vid problemlösning, exempelvis att pröva, rita bilder, göra tabeller, osv. Denna powerpoint om problemlösning visar några exempel.
