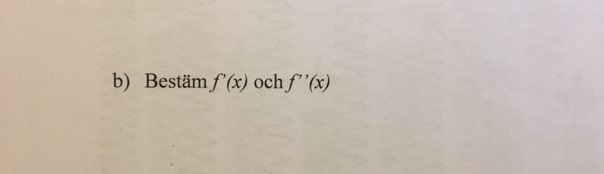Fjädrar och Hookes lag: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) |
||
| Rad 30: | Rad 30: | ||
[[File:Energia MAS.svg|thumb|Energia MAS]] | [[File:Energia MAS.svg|thumb|Energia MAS]] | ||
Integration av Hookes lag ger systemets energi ''U '' som en harmonisk, det vill säga kvadratisk, | Integration av Hookes lag ger systemets energi ''U '' som en harmonisk, det vill säga kvadratisk, potential: | ||
:<math>U = \frac12 \ k (x - x_0)^2.</math>. | :<math>U = \frac12 \ k (x - x_0)^2.</math>. | ||
eller | eller | ||
:<math>U = \frac12 \ k | :<math>U = \frac12 \ k \Delta l^2.</math>. | ||
Man kan också se energin som arean under grafen för F som funktion av <math>\Delta l</math> vilket blir en triangel med basen <math>\Delta l</math> och höjden <math>k \cdot \Delta l</math> | Man kan också se energin som arean under grafen för F som funktion av <math>\Delta l</math> vilket blir en triangel med basen <math>\Delta l</math> och höjden <math>k \cdot \Delta l</math> | ||
Versionen från 10 december 2017 kl. 21.44
| Digital bok | Pappersbok | Navigering |
|---|---|---|
| Upp till Harmonisk_svängning |
Teori
Hookes lag

Hookes lag (efter Robert Hooke) är en fysikalisk princip enligt vilken en kraft ger en deformation av mekaniska fjädrar och vissa elastiska material och är proportionell mot avvikelsen från jämviktsläget.
Antag en fjäder vars ena ända är fastsatt och vars andra ända är fritt rörlig, se figur 1. För en idealiserad fjäder är deformationen proportionell mot den kraft som verkar i fjäderns längdriktning enligt
- [math]\displaystyle{ \mathbf{F} = -k\,\mathbf{x} }[/math]
där vektorn F representerar fjäderns återställande kraft, k är fjäderkonstanten i newton per meter (N/m) och x är fjäderns avvikelse från jämviktsläget. Om fjäderns fria ända flyttas från jämviktsläget, kommer den återställande kraft som fjädern utövar att vara riktad mot jämviktsläget.
Texten ovan har hämtats där Wikipedia skriver om Hookes lag.
Energin i en fjäder

Integration av Hookes lag ger systemets energi U som en harmonisk, det vill säga kvadratisk, potential:
- [math]\displaystyle{ U = \frac12 \ k (x - x_0)^2. }[/math].
eller
- [math]\displaystyle{ U = \frac12 \ k \Delta l^2. }[/math].
Man kan också se energin som arean under grafen för F som funktion av [math]\displaystyle{ \Delta l }[/math] vilket blir en triangel med basen [math]\displaystyle{ \Delta l }[/math] och höjden [math]\displaystyle{ k \cdot \Delta l }[/math]
Experiment
Liten undersökning av fjädrar
Tag tre olika fjädrar och tre olika tyngder.
Mät elongationen för varje kombination. Skriv in dina data i Excel.
Plotta och beskriv sambandet mellan tyngd och eleongation.
Hur ser funktionen ut? Skriv en formel.
Sätt tyngden i svängning (små rörelser upp och ner).
Mät svängningstiden för tre tyngder på samma fjäder. Mät gärna tio perioder och dela med tio för högre noggrannhet.
Vilka slutsatser kan du dra?
Öva själv
| Uppgift |
|---|
| Kan du teorin om fjädrar?
[math]\displaystyle{ \alpha }[/math]Skriv formeln för Hookes lag [math]\displaystyle{ \beta }[/math] Beskriv med ord vad Hookes lag handlar om. [math]\displaystyle{ \gamma }[/math] Ange en formel för fjäderns potentiella enrgi och glöm inte att definiera ingående storheter. [math]\displaystyle{ \delta }[/math] Vad betyder begreppen:
|
Exit ticket
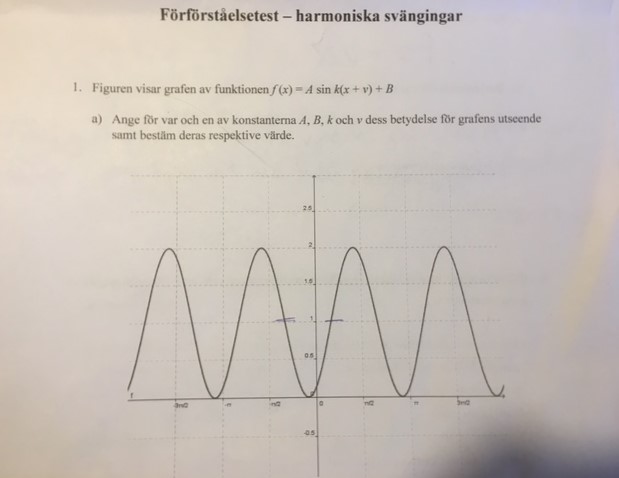
Exempellösning uppg 1