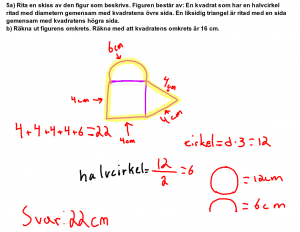
Geometri år 7 - Vinklar, fyrhörningar, trianglar, cirkelns omkrets
JMF gärna med arbetsplanen geometri år 6.
Lektion 1 - Intro
Proven. Dela ut proven. Klistra in proven i provhäftet.
nyheter. Nytt mot år sex är:
- Vinklar
- Att vi ska lära oss räkna ut cirkelns omkrets. Till detta använder vi pi.
Arbetsplan Titta på arbetsplanen.
Titta igenom inledningssidorna och diskutera frågorna där.
Bläddra igenom boken.
Anders lathund i Geometri år 7 Lathunden
Duggor. Vi kommer att ha två duggor. Se geometrisidan
Arbetstakt och beting. Det kommer att bli många korta genomgångar. Varje avsnitt i grön kurs får en genomgång. Dessutom skriver jag vilka uppgifter alla måste göra. Dessutom varvar jag detta med att ha genomgångar av innehållet i röd kurs. På dessa lektioner väljer du om du vill fortsätta med betinget från grön kurs på den tidigare lektionen eller om du vill göra rödkursuppgifter.
Geometrihistoria. Lernify
- Läs gärna: Webbmatte om Geometri
Lektion 2 - Vinklar
Genomgång läxa 3 uppgift 12. Hönsägg 55 gram. Strutsägg 2300 gram. Hur många många hönsägg motsvarar det?
Läxorna innehåller uppgifter som vi inte gått igenom. Det här är något som jag inte noterat förrän nu och förmodligen något som bokens författare också missat. Kanske är det en uppgift som hängt med sedan tidigare.
Uppgift 12 på läxa tre kräver division med tvåsiffrig nämnare och det har vi inte gått igenom och det finns inte heller förklarat i boken. Förr i tiden var det lättare med liggande stolen och liknande metoder men idag tycker vi (lärare) att eleverna kan göra detta i datorn eller med miniräknare.
Problemet är att hela kapitel 1 i boken är inriktat mot räkning utan miniräknare. De allra flesta uppgifterna förlorar sin mening om man använder miniräkanre. Uppgift nummer tolv på läxa tre har i och för sig en del av sin svårighet i att förstå uppgiften och välja räknesätt varför det kunde vara befogat att använda miniräknare men i så fall borde det stå i uppgiften.
Material. Vi behöver gradskivor.
Dema med gradskiva på tavlan.
Mål. Kunna uppskatta, mäta och beräkna vinklar, dvs
Beting. Alla ska göra alla uppgifterna på sid 46 i MD.
Lektion 3 - Vinklar igen
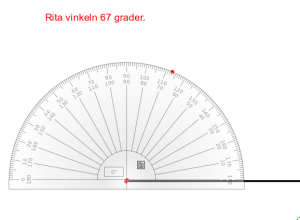
Mål
- Kunna rita en viss vinkel.
- Veta vad en spetsig, trubbig och rät vinkel är
Beting. Alla ska göra alla uppgifterna på sid 47 i MD och uppgift 6-7 på sidan 48.
Datorövning. matteva - uppskatta vinklar.
Lektion 4 - mer om vinklar (gärna två lektioner)
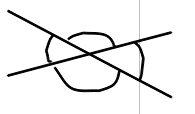
Det här hör till röd kurs. Du kan räkna fortsätta med dina uppgifter på grön kurs om du vill.
Beting över G. Röd kurs uppg 11-19.
Mål
- Känna till förhållandet mellan vinklarna som uppstår då två linjer skär varandra
Begrepp
Namnge vinklar Matte Direkt sidan 66.
Ex vinkeln BAC
Vertikalvinkel, sidovinkel och vinkelsumma. Matte Direkt sidan 67.
Bisektriser. Matte Direkt sidan 70.
Film. Fröken Matte om vinklar.
Eller denna:
Båda filmerna är från kursen Matte A på gymnasiet men det går faktiskt att förstå ändå.
lektion 5 - Beskriva trianglar
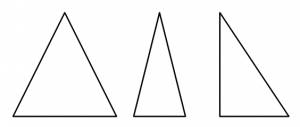
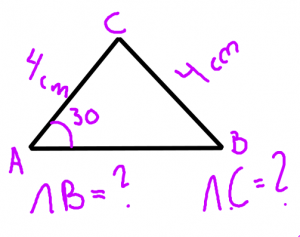
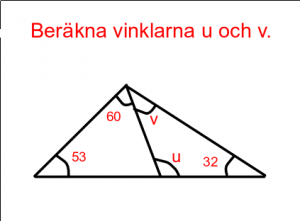
Mål
- Veta att vinkelsumman i en triangel är 180 grader och kunna utföra beräkningar baserat på detta.
- Kunna beskriva egenskaperna hos en spetsig, trubbig, liksidig, likbent och en rätvinklig triangel
Ex vilka sidor och vinklar som är lika
- Veta skillnaden mellan rätvinklig, liksidig och likbent triangel.
Ex kunna beräkna alla vinklar i en likbent triangel om toppvinkeln är 30 grader.
Genomgång Vi löser vinkeluppgiften till höger tillsammans.
Film. http://www.arstaskolan.se/index.php?option=com_hwdvideoshare&task=viewvideo&Itemid=186&video_id=228 martin om olika typer av trianglar
Den här filmen visar hur man sätter namn på vinklar och sträckor. Sedan förklarar den vad likbenta och liksidiga trianglar har för egenskaper.
Beting. Alla ska göra alla uppgifterna på sid 48-50 i MD. Det ska vara klart efter denna lektion. (sedan tidigare är man ju klar med alla uppgifter om vinklar på grön kurs)
Över G. Hur många olika trianglar kan man göra med samma omkrets (12 cm). Utmaning. Matte Direkt sidan 73. Detta är en bra uppgift. Gör den noga och redovisa så utförligt och snyggt du kan i datorn. Be om praktiskt material om diu behöver det.
Lektion 6 - Konstruera trianglar och bisektriser
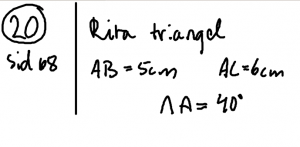
Mål. Kunna rita trianglar med hjälp av linjal, gradskiva och passare.
Mål. Kunna rita bisektriser med hjälp av linjal, gradskiva och passare.
Att göra. Fortsätt med betinget grön kurs om trianglar om du behöver det. Sid 48-50.
Överkurs. MatteDirekt sidorna 68-69 om att rita trianglar och sidan 70 om att konstruera bisektriser.
Lektion 7 - Beskriva rektangel och fyrhörningar.

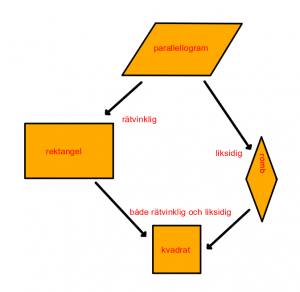
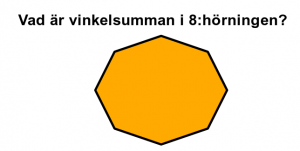
Begrepp:
Parallellogram är en fyrhörnig geometrisk figur vars motstående sidor är parallella. Specialfall av parallellogrammer är kvadrater, rektanglar och romber.
En romb är en fyrhörnig geometrisk figur vars alla sidor är lika långa. Detta betyder också att motstående sidor är parallella.
En rektangel är en fyrhörnig geometrisk figur där alla fyra vinklarna är lika stora, d.v.s. räta (90°). Motstående sidor är lika stora.
En rektangel är ett specialfall av en parallellogram. En kvadrat är ett specialfall av en rektangel.
En kvadrat är ett specialfall av romb, rektangel och parallellogram.
All text om begreppen kommer från svenska Wikipedia.
Mål. Kunna beskriva en rektangel och en kvadrat samt kunna rita dessa.
Film. martin om olika fyrhörningar
Beting. Sidan 51 (grön kurs). Om du är klar med sidan gör du överkursuppgifterna nedan.
- Geomeri åk 7 ppt. En presentation att använda vid genomgångar. Den skapades ursprungligen på ActivBoard.
Över G. Vinkelsumman i månghörningar. Matte Direkt sidan 71. Se kllippet nedan om vinkelsumman i en fyrhörning.
Över G. Parallelltrapets.
Över G. Matteva - Sortera på symmetri.
Lektion 8 - Omkretsen för fyrhörningar, mm
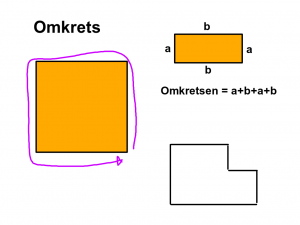
Genomgång.
- Vad är omkrets?
- Uppgift 28a
- Beting. Sidan 52 i MD.
- Extrauppgifter. Matteva om geometri.
Provet kommer att vara vecka 47, må för 7B och torsdag för 7F
Michael bondestams film behandlar omkrets men även arean för en triangel. Det är repetition från förra året.
Lektion 10 - Beskriv cirkeln och dess omkrets
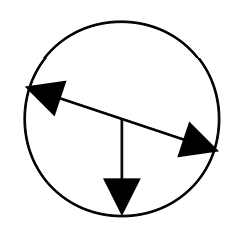
Mål.
- Kunna beskriva en cirkel (sida, radie, diameter, mittpunkt)
- Förstå vad talet Pi kommer ifrån och veta att det är en symbol för ca 3,14.
genomgång. vad är pi? genomgång - Cirkeln Cirklar och pi. En Powerpoint som beskriver nio olika övningar eller laborationer på pi. Svårighetgraden varierar från åk 6-9. Det finns ett exempel på hur två elever redovisar sitt arbete i ppt.
- Film. Martin om Pi.
- Film. martin om cirklar.
Mikael Bondestams film behandlar även arean. Det är överkurs :)
Beting. Räkna alla uppgifter på sidan 53-54. Fördjupning. Matte Direkt sidan 64-65 där pi = 3,14.
Lektion 11 - Diagnosen
Nu kommer diagnosen sent i kursen och några av er har kanske gjort den redan men vi ska ändå göra den tillsammans. Alla på en gång. Och på tid. Därefter rättar du.

.
Efter det får ni reflektera över vad ni behöver öva på. Titta på diagnosresultatet. Bläddra igenom boken och titta på wikiskola. Därefter bloggar ni era instruktioner till er själva.
Lektion 12 - Repetition - Tänk till om geometri
Genomgång
- Eleverna i en sjua gjorde varsin bild till en powerpoint som sammanfattar geometrin de jobbat med.
- Eleverna gav synpunkter på varandras bilder och vi sammanställde det till en lagom lång presentation. Dessutom innehåller den en förbättringsuppgift för kommande elever. Eleverna berättar också vad de tyckte om övningen.
- QWiki
- Powerpointfrågor - geometri.En ppt med frågor till eleverna. Den tränar begrepp och förståelse. Eleverna kan jobba en och en eller två och två och skriver sina svar i ppt-filen. Filemn kan de spara på en server och få rättad.
- Repetitionsuppgifter från lärarhandledningen som delas ut på papper.
Extrauppgifter
- Hemuppgift med fotbollar
- Läs på webbmatte.se om vinklar och geometriska begrepp
- jobba med Matteva, den finska sidan
- UR-Smart om geometri. Egentligen en lämplig introfilm.
- Webbmagistern om att mäta vinklar.
- Webbmagisterns vinkelmaskin.
Anders lathund i Geometri år 7 Lathunden
Lektion 13 - Formelsamling /sammanfattnig
- Eleverna gör en formelsamling i ppt.
- Jag ställer frågor och de svarar.
- Sedan gensvar och hoplänkning.
- Vi tittar igenom den tillsammans och gör förbättringar.
Laboration – Omkrets delat med diameter
Inledning Börja med några mätningar. Ungefär hur lång omkrets har en cirkel med diametern. Försök att rita upp cirklarna och lägg ett snöre eller måttband runt.
a)10 cm b) 7 dm c)2 m
Fortsättning Eleverna mäter omkrets och diameter på olika objekt
- De gör en tabell
- De dividerar ..
- De drar slutsatser
Genomgång av geometriprovet