Övergripande kursplan geometri
Övergripande kursplan Geometri
Du ska kunna:
• Omvandla längdenheter
Skriv 3m som mm
• Lösa uppgifter som handlar om skala
Rita pilen i skala 1:3

• Begreppen triangel, rektangel och kvadrat samt kunna rita dessa
• Mäta och rita vinklar med hjälp av gradskiva
• Känna igen trubbiga, spetsiga och räta vinklar
• Räkna ut en figurs omkrets

Alt 1: 2•8 + 2•3=22 cm
Alt 2: 8+8+3+3= 22 cm
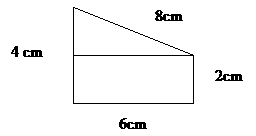
• Räkna ut en sammansatt figurs omkrets
Omkretsen: 6+2+8+4=20 cm
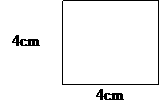
• Beräkna arean av en kvadrat
Arean: s • s = 4 •4 = 16 cm
• Beräkna arean av en rektangel
Area: b • h = 6 • 4 = 24 cm
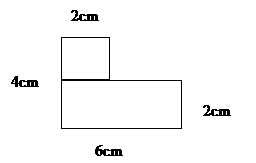
• Beräkna arean av sammansatta figurer
Arean: 6 • 2 + 2 • 2 = 16 cm
• Beräkna arean av en triangel
Arean: Bas • Höjden = 3 • 8/2 = 12

• Kunna rita figurer utifrån given omkrets och area.
Exempelvis
. Rita en rektangel med omkretsen 14 cm.
Rita en triangel med arean 12 cm.
• Förstå vart talet p kommer ifrån och veta att det är ca 3,14.
• Kunna utföra enhetsomvandlingar
Exempelvis
Skriv som meter a) 13,5 dm b) 420 cm c) 1,5 km
Skriv som dm2 a) 1 m2 b) 250 cm2 c) 10 cm2
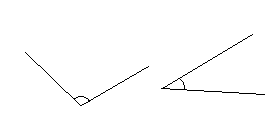
• Kunna uppskatta, mäta och beräkna vinklar
Exempelvis
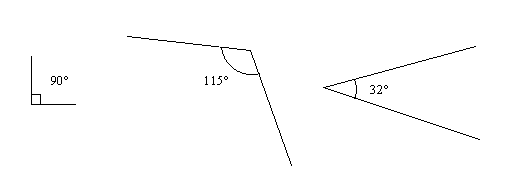
Uppskatta storleken på vinklarna och mät sedan med gradskiva.
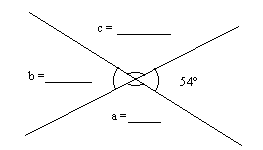
Beräkna utan att mäta vinklarnas storlek i figuren
• Veta skillnaden mellan rät, trubbig och spetsiga vinklar.
• Känna till att triangelns vinkelsumma är 180 och kunna tillämpa det.
T.ex. Beräkna vinkeln C
• Veta skillnaden mellan liksidig, rätvinklig och likbenta trianglar.
T.ex. Rita en liksidig triangel
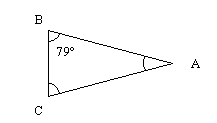
Beräkna vinkeln A i den likbenta triangeln. Mer än godkänd
• Kunna lösa svårare uppgifter med area och omkrets.
t.ex. Beräkna priset per kvadratmeter för plastfolien. Avrunda till hela kronor.
• Kunna lösa svårare uppgifter med triangelns vinklar.
T.ex. Beräkna de okända vinklarna
- veta vad skala är
- kunna göra förstoringar / förminskningar i given skala utifrån enkla föremål
T.ex. rita rektangeln i skala 1:2
- utifrån kartor / ritningar beräkna verkliga längder
T.ex. Pilen är ritad i skala 4:1 Hur lång är den i verkligheten?
- kunna ange skalan
T.ex. I vilken skala är det stora hjärtat ritad i?
För väl godkänt ska du:
- kunna lösa svårare uppgifter med triangelns vinklar
T.ex. Vinkeln BCD är 21° . Triangeln ACD är liksidig. Hur stor är vinkeln CBD? T.ex. Beräkna de okända vinklarna.

- veta vad cirkelsektor, båge och medelpunktsvinkel är
- kunna använda Pythagoras sats och kunna namnge sidorna i en rätsidig triangel
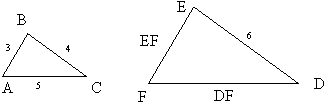
- kunna lösa problem med hjälp av likformighet
T.ex. Triangel ABC är likformig med triangel DEF . Beräkna med hjälp av likformighet sidorna EF DF.
För mycket väl godkänt ska du:
- kunna formulera och lösa olika typer av problem samt jämföra och värdera olika metoders för- och nackdelar
- visa säkerhet i beräkningar och problemlösningsarbete
- kunna använda generella strategier samt analysera och redovisa strukturerat med korrekt matematiskt språk
- Kunna utföra enhetsomvandlingar.
T.ex. Skriv som meter a) 13,5 dm b) 420 cm c) 1,5 km Skriv som dm2 a) 1 m2 b) 250 cm2 c) 10 cm2 Skriv som liter a) 1 dm3 b) 1 m3 c) 20 cm3
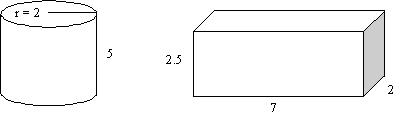
- Kunna beräkna volymen av olika rätblock och cylindrar
T.ex. Beräkna volymen på figurerna


För Väl godkänt
- Kunna beskriva en parallellogram, romb, pyramid, klot, kon och ett prisma.
- Kunna beräkna arean på en parallellogram.
- Kunna beräkna volym av klot, prisma, kon, och pyramid.