Beräkna integraler: Skillnad mellan sidversioner

VisuellWikitext

Nuvarande version från 21 april 2016 kl. 10.43

Ma3C: Integraler , sidan ss

Sid 207-213 - Beräkna integraler

Mål för undervisningen

Denna lektion kommer du att lära dig hur du beräknar integraler.

Definition

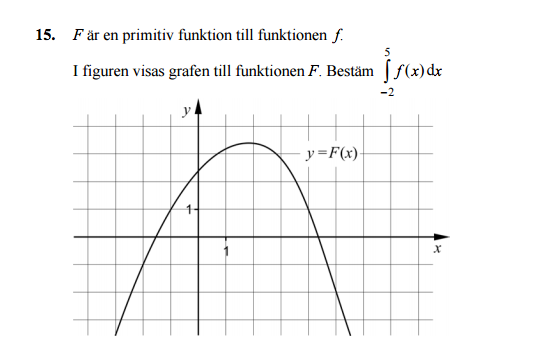
För en funktion f som är beroende av variabeln x och kontinuerlig på [a,b] beräknas integralen av f på följande vis:

[math]\displaystyle{ \int_a^b f(x)dx = F(b) - F(a) }[/math]

där F är en primitiv funktion till f.

Exempel från fysiken

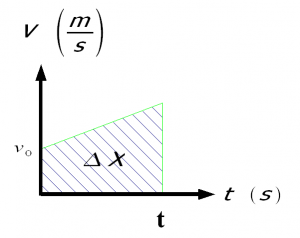
Jämför med mekaniken, sträckan är arean under en vt-graf.

Begynnelsehastighet och förändring av hastigheten

Acceleration är lika med hastighetsökningen per sekund. Vid en konstant acceleration a, gäller då att:

v = v₀ + at

v₀ är hastigheten vid start och t är så klart tiden från start.

Exempel: Fru Gran tapper en blomkruka genom fönstret. Vilken hastighet har den 1,5 sekunder senare?

t = 1,5 s. a = g = 9,82 m/s².

v = at = 9,82 m/s² * 1,5 s = 14,7 m/s

Arean

Arean under en vt-graf är lika med sträckan. Tänk att medelhastigheten * tiden = sträckan.

v_m = (v_efter - v_före) / 2

Men sträckan är ju v_m * t och det kan man ju se som arean av cen triangel som bildas av grafen i vt-diagrammet.

naturvetenskap.org ger en beskrivning.

Animering av sträcka under vt-kurva

<swf width="600" height="400">/images/FysikA_s_e_area_u_vt_kurva_2.swf</swf>

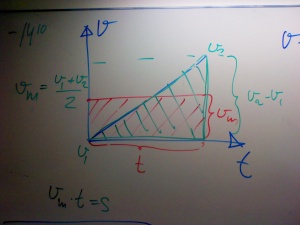
Khan om sträcka = area under vt-kurva

Sträckan

s = v₀t + at²/2

Geometriskt bevis

Wikipedia: Fundamental_theorem_of_calculus

For a continuous function y = f(x) whose graph is plotted as a curve, each value of x has a corresponding area function A(x), representing the area beneath the curve between 0 and x. The function A(x) may not be known, but it is given that it represents the area under the curve.

The area under the curve between x and x + h could be computed by finding the area between 0 and x + h, then subtracting the area between 0 and x. In other words, the area of this “sliver” would be A(x + h) − A(x).

There is another way to estimate the area of this same sliver. As shown in the accompanying figure, h is multiplied by f(x) to find the area of a rectangle that is approximately the same size as this sliver. So:

[math]\displaystyle{ A(x+h)-A(x) \approx f(x)h }[/math]

In fact, this estimate becomes a perfect equality if we add the red portion of the "excess" area shown in the diagram. So:

[math]\displaystyle{ A(x+h)-A(x)=f(x)h+(\text{Red Excess}) }[/math]

Rearranging terms:

[math]\displaystyle{ f(x) = \frac{A(x+h)-A(x)}{h} - \frac{\text{Red Excess}}{h} }[/math].

As h approaches 0 in the limit, the last fraction can be shown to go to zero, which implies

[math]\displaystyle{ f(x) = \lim_{h\to 0}\frac{A(x+h)-A(x)}{h}. }[/math]

This implies f(x) = A′(x). That is, the derivative of the area function A(x) exists and is the original function f(x); so, the area function is simply an antiderivative of the original function. Computing the derivative of a function and “finding the area” under its curve are "opposite" operations. This is the crux of the Fundamental Theorem of Calculus.

Läs gärna vad Wikipedia skriver om Analysens_fundamentalsats även om det är på en hög nivå för det är så häftigt.

Förklaring med hjälp av Riemannsumman

Integral - Riemannsumma

Kan man tänka sig någon trevlig frågeställning som ingång till integralerna?

Börja med att visa Riemannsumman för att ta reda på arean under en graf.

GeoGebra om Riemannsumma in här

Övning Riemannsumma i GGb

Uppgift

laborera själv i Geogebra

Denna GGB ger dig möjlighet att flytta stapeln och att testa olika funktioner.

Du kan ändra på antalet staplar och se hur det påverkar beräkningen.

Här är GGB:n:

Vad lärde du dig av denna övning?

uppg 2

Testa denna: http://www.geogebratube.org/student/m11330

Hur hanteras negativa areor?

Uppg 3

Man kan skapa Riemannsummor mellan två funktioner:

Flippa = Gör detta till nästa lektion!

Lös uppgifterna 4221 - 4240. Läs på om Arean av ett område mellan två kurvor.

Exit card

En kunskapskontroll lämplig för lektionesns avslutning.

Uppgift:

Facit: (klicka expandera till höger)

@@ Rad 4: / Rad 4: @@
 Denna lektion kommer du att lära dig hur du beräknar integraler.
 }}
-== Mekaniken ==
-Jämför med mekaniken, sträckan är arean under en vt-graf.
 {{defruta |
@@ Rad 17: / Rad 13: @@
 där ''F'' är en primitiv funktion till ''f''.
 }}
+== Exempel från fysiken ==
+[[Fil:Trapez_vt.png|thumb|Sträckan = arean under en vt-graf. CC By Tharbad]]
+Jämför med mekaniken, sträckan är arean under en vt-graf.
+=== Begynnelsehastighet och förändring av hastigheten ===
+Acceleration är lika med hastighetsökningen per sekund. Vid en konstant acceleration ''a'', gäller då att:
+: v = v<sub>0</sub> + at
+''v<sub>0</sub>'' är hastigheten vid start och ''t'' är så klart tiden från start.
+Exempel: Fru Gran tapper en blomkruka genom fönstret. Vilken hastighet har den 1,5 sekunder senare?
+: t = 1,5 s. a = g = 9,82 m/s<sup>2</sup>.
+: v = at = 9,82 m/s<sup>2</sup> * 1,5 s = 14,7 m/s
+=== Arean ===
+Arean under en vt-graf är lika med sträckan. Tänk att medelhastigheten * tiden = sträckan.
+: v<sub>m</sub> = (v<sub>efter</sub> - v<sub>före</sub>) / 2
+Men sträckan är ju v<sub>m</sub> * t och det kan man ju se som arean av cen triangel som bildas av grafen i vt-diagrammet.
+[http://www.naturvetenskap.org/index.php?option=com_content&view=article&id=87&Itemid=94 naturvetenskap.org ger en beskrivning.]
+=== Animering av sträcka under vt-kurva ===
+<swf width="600" height="400">/images/FysikA_s_e_area_u_vt_kurva_2.swf</swf>
+[[Fil:S_area-vt-graf.jpg|thumb]]
+[http://www.khanacademy.org/video/why-distance-is-area-under-velocity-time-line?playlist=Physics Khan om sträcka = area under  vt-kurva]
+=== Sträckan ===
+: s = v<sub>0</sub>t + at<sup>2</sup>/2
+{{clear}}
 == Geometriskt bevis ==
@@ Rad 40: / Rad 78: @@
 :<math>f(x) = \frac{A(x+h)-A(x)}{h} - \frac{\text{Red Excess}}{h}</math>.
-As ''h'' approaches 0 in the [[limit of a function|limit]], the last fraction can be shown to go to zero.<ref>[[Lipman Bers|Bers, Lipman]]. ''Calculus'', pp. 180-181 (Holt, Rinehart and Winston (1976).</ref> This is true because the area of the red portion of excess region is less than or equal to the area of the tiny black-bordered rectangle.  More precisely,
+As ''h'' approaches 0 in the limit, the last fraction can be shown to go to zero, which implies
-:<math>\left|f(x) - \frac{A(x+h) - A(x)}{h}\right| \le \frac{|\text{Red Excess}|}{h} \le \frac{h|f(x+h) - f(x)|}{h} = |f(x+h) - f(x)|.</math>
-By the continuity of ''f'', the latter expression tends to zero as ''h'' does.  Therefore the left-hand side tends to zero as ''h'' does, which implies
 :<math>f(x) = \lim_{h\to 0}\frac{A(x+h)-A(x)}{h}.</math>
-This implies {{nowrap|''f''(''x'') {{=}} ''A''′(''x'')}}. That is, the derivative of the area function ''A''(''x'') exists and is the original function ''f''(''x''); so, the area function is simply an [[antiderivative]] of the original function.  Computing the derivative of a function and “finding the area” under its curve are "opposite" operations. This is the crux of the Fundamental Theorem of Calculus.
+This implies {{nowrap|''f''(''x'') {{=}} ''A''′(''x'')}}. That is, the derivative of the area function ''A''(''x'') exists and is the original function ''f''(''x''); so, the area function is simply an antiderivative of the original function.  Computing the derivative of a function and “finding the area” under its curve are "opposite" operations. This is the crux of the Fundamental Theorem of Calculus.
 Läs gärna vad {{svwp | Analysens_fundamentalsats}} även om det är på en hög nivå för det är så häftigt.
@@ Rad 87: / Rad 125: @@
 {{clear}}
 {{flipped | Lös uppgifterna 4221 - 4240. Läs på om [[Arean av ett område mellan två kurvor]].
+}}
+== Exit card ==
+En kunskapskontroll lämplig för lektionesns avslutning.
+{{uppgfacit |
+[[Fil:NpMa3c_ht_2012_uppgift_15.png | 600px |vänster]]
+|
+[[Fil:NpMa3c_ht_2012_Uppgift_15_-_facit.png | 600px |vänster]]
 }}

Beräkna integraler: Skillnad mellan sidversioner

Nuvarande version från 21 april 2016 kl. 10.43

Innehåll

Exempel från fysiken