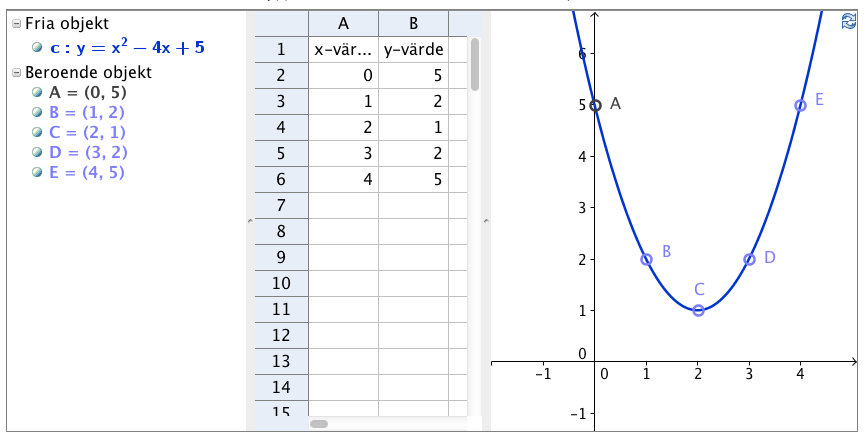
Andragradsfunktionens graf
Begrepp och egenskaper hos andragradsfunktionern
vertex är kurvans vändpunkt
nollställen
positivt före x2-termen betyder minimipunkt
negativt före x2-termen betyder maximipunkt
symmetrilinje genom vertex
Hur ritar man en parabel om man vet funktionen?
Man gör en värde tabell. Tag ett lämpligt x-värde och skriv i tabellens x-kolumn. Räkna ut vad y blir genom att sätta in x-värdet i funktion. Skriv y-värdet i dess kolumn. Nu har du det första talparet. Upprepa med ett antal lämpliga x-värden tills du fått minst tre gärna fem talpar. Det är viktigt att du väljer talparen så att du hittar vertex (min- eller maxpunkten).
Om du har funktionen i den allmänna formen y(x) = ax2 + bx + c kan det vara bra att kvadratkomplettera.
Fördjupning
Det kan vara intressant att som bakgrund titta på denna sida om kägelsnitt.