Algebra 2C
Kapitel 1 i boken Matematik 2C innehåller 16 delar vilket rimligen bör ta omkring 16 lektionstillfällen eller fyra veckor i anspråk.
Repetition
Varför ska man lära sig algebra?
Mål för wikiskola på denna sida
Ett mål för denna kurs är att varje avsnitt om möjligt ska ha ett videoklipp med någon som förklarar, relevant länk till Khan samt en GGB el dyl som anknyter till bokens teoridel. Dessutom vore det fint med några egna övningsuppgifter och någon datorövning.
Intro
Kuriosa: Grafer på Google
Algebraintroti boken på sid 3
Gerolamo Cardano funderade över lösingen till följande ekvation
Kan vi dela talet 8 i två delar så att deras produkt blir 25? x(8-x) = 25
Ekvationen har följande rötter:
x = 4 + rot(-9) x = 4 - rot(-9)
Ekvationen kan skrivas om på detta sätt:
8x - x2 = 25
x2 - 8x + 25 = 0
Men vad är roten ur -9? Det är ett imagint tal, som skrivs 3i. Kolla gärna Wolfram Alpha för en lösning till ekvationen ovan
Förenkling av uttryck
Sats: Distributiva lagen
a(b+c) = ab + ac
Ekvationer
Vid lösning av ekvationer kan du tänka att det är tillåtet att göra samma sak på båda sidor av likhetstecknet. Du kan addera samma sak på båda sidorna. Eller subtrahera samma sak på båda sidorna. På samma sätt kan du multiplicera eller dividera med samma sak på båda sidorna.
Detta kan du använda för att förkorta bort något på ena sidan och resultatet blir att den saken byter upp på andra sidan men med motsatt tecken (plus blir minus osv).
På denna sida från Matteboken.se finns en förklaring skriva om hur man ändrar i ekvationer på detta sätt. Titta gärna på filmen på sidan också.
När man får kläm på det här sättet att ändra i ekvationer brukar man helt enkelt flytta över saker till andra sidan och byta tecken. På så sätt kan man ändra en ekvation så att man får sitt x (eller vilken variabel man nu vill lösa ut) ensamt på en sida.
Kvadrerings- och konjugatregler
Parentesmultiplikation
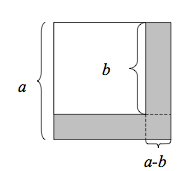
Multiplikationen är både algebra och geometri
Hur funkar det om man multiplicerar två parenteser med varandra?
Först inleder vi med ett exempel med siffror
En övning som visar exemplet nedan i bilder. Ett tal kan delas upp i sin entalsdel och sin tiotalsdel innan en multiplikation. PowerPoint. Gånger av tvåsiffriga tal visas med hjälp av bilder. Detta är ett exempel från grundskolan. Det syns till höger.
exempelvis 12*13=(10+2)*(10+3)=100+30+20+6.
Repetition aritmetik: Pappersövning i skriftlig huvudräkning.
Och nu med bokstäver

Tänk sedan att du gör samma sak med bokstäver
(a+b)(c+d)=ac+ad+bc+bd
<ggb_applet width="796" height="511" version="4.0" ggbBase64="UEsDBBQACAgIAChaLEAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAAoWixAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1b747bNhL/nD4FoQ+HXWxsi9T/nLdFk7uiAZImQHKHw30pKIm2GUuiKlJeb9DHuXuSvtgNScmW7U32T5Oc10E2FMXhDGfmNzMkV5n+sC4LtGKN5KK6dPDYdRCrMpHzan7ptGo2ip0fvv9uOmdiztKGoploSqouHV9T8vzSmSVhMpvFeJRnLBr5LItHSZ6kozwnmEUsSGgWOQitJX9WiV9oyWRNM/YuW7CSvhIZVUbwQqn62WRydXU17kWNRTOfzOfpeC1zB8EyK3npdA/PgN3OpCvPkBPXxZN/vX5l2Y94JRWtMuYgrULLv//uyfSKV7m4Qlc8V4tLJ3Z9By0Yny9Ap9APHTTRRDUYpGaZ4ismYeqga3RWZe0YMlrp8Sf2CRUbdRyU8xXPWXPpuGPiRhHGvk+iOHTDJAwcJBrOKtUR407opGc3XXF2ZfnqJyMSlqmEKFKqWaLff0fEJS56qhtsGwJNGNoh175zPdsQ2/i2CSyNb6f7ltS3NL6l8T0HrbjkacHAw7SQYEJezRpw36Yv1XXBzHq6F1v18VPQSfKPQIxdwIm1uek81T8h/Ph6YLKrJB5IVU17T6G9yCgJ7y6S/ClFvY2aYXQokwSfUDP8jFCr9130xMHAtCDK/DU/BxK9z6m5L9H2bxPoxVpgFPs3Cgz9b6LidNKHyrSLDiQXmrZDj2Kl1PHiJShINOwxCiA2wghQHiCcQBMRBNGAcID8ALo4RqFuI+RFMOAjD8VI02EPmeAIYvjHjwyzEAXATL+NICYRBkE+CjyETUz5CCIJmbiEGCUeUAQBCmCSFo+JZuGFyA+h58XIhzXqkIwwEHowEfogniAPI09PxhEiIQo1P+zrUA9jvXRgSVDoohBrhhDVENE2moE+Rp7Wps9rvKpbtWOirMz7RyXqjS+AGvLRNu3Z/LSTFZ9MC5qyAgrFO+1JhFa00BFhBM1EpVDvRGLfzRtaL3gm3zGlYJZEH+iKvqKKrX8CatnLNrSZqOTbRqgXomjLSiKUicLdrFkUePBMNquGjjcY8IcDwWAgHDxHN8oVMIJayUC+aGRPTvP8pabYpgaw5JuquH7eMLqsBd9VYzoxNWfK2qzgOafVPwGsWoq2C+pLkElXfQnyY69fiGjyd9cSEIzW/2aNgFSFydj3SEKwG/ok9BIHXdsRL/TGQRBjD/s4IJHnQYmRGdWxFwXjIIxiQlwvCeMw0ZO6oZCMcRyGOHSjIPEJDgIrmq02HqJrtlV23ph6v+28lM9FsX1l9H9Ba9U2ZvcAybHRWv1YzQtmMGIiG0pztkzF+p0Fh2d5vb+uoefaFaRzY3cEuYHoAj3v2hTafpV6aRsq19C4hsLt0cbzzThOiKEwbWpbQwXwtUvrVMW9mtjtxXBpMprrdHHTZysNfl3p24qrV31H8Wy5VVVP+KUtU7aB0C5P/KV4Tid7GJsuWVOxooM0OLMVrbQROkB7zjJeQtcOdCah2l3/gAXYtzmbN6xfeGF2ZtZgZtQdovXgtWH1UyPKl9XqPWBhbwHTSb/KqcwaXmvMoRTKwJJtUZVzSaGK5MN5OgZB9UxXCzCP0qY5oxfp+Vl2kZ9DnLZqIcDtP//x3yWt0N8L2IlJxefADdIN2NRsBEWzlAvG1Hu2VoimYgUjr9tC8brgS1OJEF0h2ZYlgIhXokQ1bWDbxiRr0B//aWCjDK9VI/J22a2kKNByRfOG6QiQDQP1m4oikS3QUlQf2jlV8JIV1RhgyArteqMQK1gJnJEyUVC1JTDINnjIfiVmxWC9tjMwGYfWxBoOSKQfIC1vKredtcUbDH8iUhAt6gXVm1TcxQO9BuWGPjTcXou8E9zRyULvblHJK8OmpGuoz8AulZCwFWzvATPVdntvF9YlPNga6cMDzPBD/XANqQIH+mnG12xTjsCD/CNgl+7osg1YBbVkCRtmaTZxqssf5uFnnues2iyWVoBy4yFIp7XVFkElYzYEN1Nr0N5krgFCO8/c6qP00Ed47J+Cj+LORyR8BD5a1w1I02w6C/8NzrNr4HfmPkXgo/OelSlWdp+z69huYDP9wIG7ufpmD2IS2Hqj265qbf3o3tGPw+QqtS/czhUaWeijPa7b86petC6oO5sw+3YvK98d0vRkIR31kMb+I4T08x7S4KCnyL0vpJ8fFaQNlK87aH8JSB+Y68WOuR6QA148zGBDyH9hY32d+N/V+sf/s9Z3ih58U/TclDG/FLwyUZa0ylFlLjLeiuJ6Lipne7SmrrYcotiEKSUGftTThcSaqlU9GU0tHbV0aWoJs19BKQpH19TK7iTe4C0re5OtU+ehieq+yRwHnvFygB+cz2+BomRz3dsqdwjGP7fOL1aCt6weYHj2W2WnSHu84yUcPTKuNlgpNLRfwpGjkcycdg7PcEvGan14flO9b2gl9f28pRmcDe9o5TS9xcwDsV/bzqPDwpAEyfBPdDJ21yF/NIbvAT7aFpmTNfxteP92aWUf7Y8rrdylKj631e6MoguU9RtXXfi2b9JzWwLPqHneL5hpZllkdh6zxDNbLef3q5bA63SrZXY0sO6Tib6uenyw/ryV2fHk7INiGfTXgydg59nx2HlTG3s8e+PQO9HaOD8es++je3RCW5L9S7e82wvuXLp53/LS7c1sJpnSdje/YdQXbF//Rq6/ZPZCcvQ3cnfZ7Zjr5vN+y9M9k+4Z9jvg5n6z4w7eHNwR5JbFws7mdsoHu+XJ73lBkJ/wlmdxPNlq/4bglLLVvtn58ZgdzOy5O3+8vfuD+OB3/o/W7h+Ox+4H9wXeOIpPxtD50RylboH34zpZ3amE0mEJ1XcEwzLa9XdLKf1MKc26UlpYDqWdUtlSWt+vlGanXEqL48st/XFrdMLnrfJ4zH5bKQ3GZGcUn4wTquNxwsFdQzR2yWlavT4eq9+C/NFj20UefA2hP3bE3RcRf/mtFeqvZ+lFfn5GL7JzdAnn9os0u6D5RZbbUcNx130KWDi7/B7kv09dT9zTeeZTc8kaPtt+lt39nwynN3RHKhVt1Fv9O35k8hzIcv2YRG4SxYHv4iDRc+xmliS+G2E3ICQK/QgPvx4YWngy/BbVfPLd/fel7/8HUEsHCKNA+swOCQAAWzUAAFBLAQIUABQACAgIAChaLEBFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgAKFosQKNA+swOCQAAWzUAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACmCQAAAAA=" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
Hela filen kan laddas ner här.
Bevis som utgår från distributiva lagen
x(c+d) = xc+xd
Antag att x = a+b och sätt in i uttrycket ovan.
(a+b)c+(a+b)d c(a+b)+d(a+b) ca+cb+da+db ac+bc+ad+bd V.S.B.
Läs om distrributiva lagen på wwebbmatte.
Kvadreringsregeln
Första och andra kvadreringsreglerna
Kvadreringsreglerna är regler i algebran om hur man utvecklar uttrycken
| [math]\displaystyle{ \ (a+b)^2=a^2+2ab+b^2 }[/math] | (Första kvadreringsregeln) |
| [math]\displaystyle{ \ (a-b)^2=a^2-2ab+b^2 }[/math] | (Andra kvadreringsregeln) |
Texten i ovanstående avsnitt kommer från Wikipedia.se
Förklaring (a-b)2 = (a-b)(a-b) = a2-ab-ba+b2 = ( och ab = ba ) a2-2ab+b2 V.S.B.
Länkar:
Bondestam respektive Wille på Mattecentrum om kvadreringsregeln:
WolframAlpha Widget
Här kan du testa att låta datorn göra parentesmultiplikation:
{{#widget:WolframAlpha|id=c3f53c80c93fa003e2f8f54c64e0e386}}
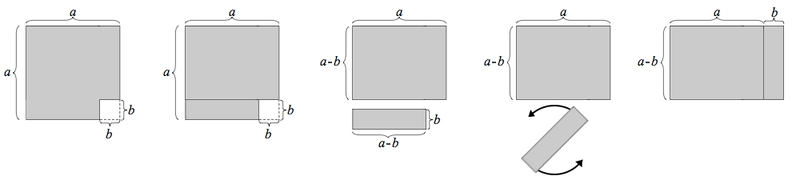
Konjugatregeln
Konjugatregeln
- Så här ser den ut:
- a2-b2 = (a-b)(a+b)
- [math]\displaystyle{ (a-b)\cdot(a+b) }[/math]
- [math]\displaystyle{ = a^2 +a\cdot b -a\cdot b -b^2 }[/math]
- vi kan stryka ab - ba = ab - ab = 0:
- [math]\displaystyle{ = a^2-b^2 }[/math]
- V.S.B.
Film
Bondestam (tv) respektive Matteboken (th) förklarar:
Geometriskt bevis av konjugatregeln
Första beviset
Andra beviset
Visualisering
Här gäller: [math]\displaystyle{ (x-y)\cdot(x+y) = x^2 - y^2 }[/math] Denna är gjord med Geogebra, sparad som animerad gif, upladdad till WIKIMEDIA COMMONS och länkad hit. [math]\displaystyle{ (a - b)\cdot(a + b) = a^2 - b^2 }[/math]
Uppgifter
Övningar (utan räknare)
1. [math]\displaystyle{ 1992\cdot 2008 = ? }[/math] 2. Lös [math]\displaystyle{ x^2-1=0 }[/math] för alla reella x.
Tips : Använd konjugatregeln och nollregeln för ekvationen.
Webbmatte
Diagnos 11
Rättelse: I lösningen till uppgift 6 finns tyvärr inte med att lösningen även har en negativ rot. Detta kommer vi att gå in noggrannare på i avsnitt 1.3 som behandlar andragradsekvationer.
Ekvationer med x2-term
Repetition
Uppgiften från förra lektionen att göra Khan ett tagskulle kunna vara en vettig repetition av föregående vecka.
Intro
Detta avsnitt handlar om ingenting kan man säga. Det handlar nämligen om ekvationer med x2-termer som försvinner vid förenklingen.
Räkna uppgifterna: 1245-1258
- Uppgift 1251: Här gör du skissen i GeoGebra.
- Uppgift 1257: Läs om en Ellips på Wikipedia.
- Pröva att göra en ellips i GeoGebra. Ledining skriv in ekvationen (x/a)^2+(y/b)^2=1. Välj själv värden på a och b.
- Sök på Ellipse på GeoGebraTube.org. Inte ett facit till ellipsen.
- Titta på en ellips i Wolfram|Alpha. Skriv in en formel eller skriv ordet Ellipse. fuskväg
Andragradsekvationer
Vi repeterar föregående avsnitt genom denna övning:
Övning: Pascals triangel
Gör övningen på sidan 24-25. Titta även på Wikipedia om Pascals triangel.
Inlämning: Vi gör övningen på uppkopierat papper med inlämning och rättning.
När du är klar med uppgiften jobbar du med Khan Academy. Länkar finns på föregående avsnitt.
Lösning: Så här utvecklar du (a+b)4
Länkar:
Här finns lite om Pascals triangel ochidéer om triangeln. Här finns trianglar att skriva ut m.m. Illustration av normalfördelning finns här.
Enkla andragradsekvationer
Den här behöver man fundera på en stund. Quadratic equations in early Baghdad
Även nu har vi att göra med andragradsekvationer som är enkla fall av den fullständiga ekvationen.
Antingen förkortas x-termerna bort så att man får kvadrattermer kvar att ta roten ur
eller
så har man ett kvadraten på ett binom (ett parentesuttryck upphöjt till två) som man tar roten ur.
I båda fallen blir det en positiv och en negativ rot som svar (eller cdel av svaret men det blir inga imaginära tal eller komplexa rötter i detta avsnitt.
Kvadratkomplettering
Uppgift: Khan Academy
Lös dessa Khan, relativt enkla andragradsekvationer. De kan lösas genom att gissa eller faktorisera.
Härledning av rotformeln
[math]\displaystyle{ ax^2+bx+c = 0, a \ne 0 }[/math] Vi multiplicerar båda sidor med [math]\displaystyle{ 4a \ne 0 }[/math] [math]\displaystyle{ 4a^2x^2 + 4abx + 4ac = 0 }[/math] vi subtraherar [math]\displaystyle{ 4ac }[/math] från bägge sidor och skriver om [math]\displaystyle{ (2ax)^2 + 4abx = -4ac }[/math] då ser vi att det fattas [math]\displaystyle{ b^2 }[/math] för kvadratkomplettering - adderas till bägge sidor [math]\displaystyle{ (2ax)^2 + 2(2ax)b + b^2 = b^2-4ac }[/math] [math]\displaystyle{ (2ax + b)^2 = b^2-4ac }[/math] [math]\displaystyle{ D = b^2-4ac }[/math] D kallas för diskriminanten. Om den är positiv eller noll så har vi en lösning. Om den är lika med noll blir det en dubbelrot annars blir det två reella rötter. Om diskriminanten är mindre än noll saknas reella lösningar. Vi löser vidare så här: [math]\displaystyle{ 2ax + b = \pm \sqrt{b^2-4ac} }[/math] Vi subtraherar [math]\displaystyle{ b }[/math] från bägge sidor. [math]\displaystyle{ 2ax = - b \pm \sqrt{b^2-4ac} }[/math] Vi dividerar med [math]\displaystyle{ 2a \ne 0 }[/math] : [math]\displaystyle{ x = \frac{-b\pm \sqrt{b^2-4ac}}{2a} }[/math] man kan sedan konstarea att : [math]\displaystyle{ x_1 = \frac{-b - \sqrt{b^2-4ac}}{2a} }[/math] och [math]\displaystyle{ x_2 = \frac{-b + \sqrt{b^2-4ac}}{2a} }[/math] Nu är vi klara.
Ibland kan det vara bra att veta att man om reella rötter saknas D < 0
löser de komplexa (imaginära) rötterna så här :
[math]\displaystyle{ z = \frac{-b\pm i\cdot \sqrt{4ac-b^2}}{2a} }[/math]
Fullständiga andragradsekvationer
pq-formeln
http://www.youtube.com/watch?v=eQZEtWY_4kE&feature=g-all pq-formeln
x2+px+q=0 x=-p/2+-((p/2)2-q)0.5
The last editor of this page did not have the right to Embed PDFs into pages.
Se en film med Michael Bondestam:
Räkna själv
Lösning: 1339 har jag gjort i ggb och den finns på hårddisken.
Mario om nytan med andragradsekvationer:
Andragradsekvationer och rötter
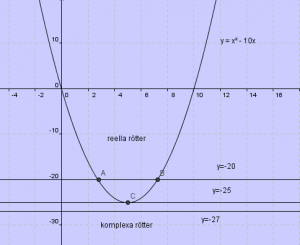
En andragradsekvation kan ha två reella rötter eller en dubbelrot eller två komplexa rötter
Detta är på sid 35-37 i boken.
Diagnosen
Resultatet på diagnosen var inte bra. Ni behöver räkna mer! Från och med nu gäller ett beting för varje lektion. Det är uppgifter som ni måste göra och visa upp. Om ni inte har godkända upvisade uppgifter från någon lektion måste ni gå på extramatten. Betinget är att göra alla svarta uppgifter.
Genomgång av diagnosen: Facit till Diagnos 12
Komplexa tal
Teori
Roten ur -1 = i. i2 = -1
Imaginärdel, realdel
z = a + bi
Läs mer: Komplexa tal på wikipedia
Vad ska man ha komplexa tal till?
- Komplexa tal används när man räknar på växelström.
- Titta på denna ppt från Uppsala.
- j-omegametoden
Komplexa rötter
x2 = -16 har ingen reell rot men däremot två komplexa. Det beror på att lösningen är roten ut ett negativt tal. Roten ur -16 är +4i respektive -4i.
x2+3x+16=0 har också två komplexa rötter fast här beror varje rot av både en realdel och en imaginärdel.
Rotekvationer
Teori
Rotekvationer innehåller x-termer och roten ur x-termer. Man löser dem genom att kvadrera båda leden.
Viktigt att kolla om man har falska rötter.
Berätta om SI
Vi har SI-lektioner på onsdagar 16.30.
Supplemental Instruction- möten är ett komplement till övriga undervisningsmoment som föreläsningar och övningar. På SI-möten som hålls av en äldre elektroteknolog får du möjlighet att lära dig att bearbeta kursinnehållet för att öka förståelsen. SI-ledaren är i detta avseende inte en lärare utan en mötesledare för studenterna. På SI-möten lär sig studenterna att själva arbeta med kursen med målet att öka sin förståelse. SI-ledaren är i detta avseende inte en lärare utan snarare en mentor för studenterna.
Meningen är att studenterna med hjälp av SI-ledaren lär sig terminologin inom ämnet, att själva prioritera inom kursen och att angripa problem. Målsättningen är att denna träning skall ge studenterna en metodik som de kan ha stor nytta av i senare kurser. Supplemental Instruction är ingen stödundervisning utan syftar till att förbättra alla studenters studieteknik och analytiska förmåga och därmed förbättra studieresultaten.
Film
Rotekvationer med hjälp av substitution kunde vara ett alternativ att titta på.
Problemlösning med ekvationer
Professionell matte
Har ni tänkt på att det är ett tag sedan vi gjorde matte som man har nytta av i vardagen? Kvadreingsregeln, konjugatregeln, kvadratkompletteringen och pq-formel hör inte till vardagsmatten. De hör till den professionella matten. Sådan matte som ingenjörer använder.
Vad ska man ha andragradsekvationer till?
De används i spel till exempel.
- Wikipedia om projectile motion
- Här finns länkar om fysikmotorn bakom Angry Birds och mycket annat
- Det finns ett exempel med två bollar som faller och där den ena även far i x-led. Banan beskriver en parabel och det är ett klassiskt exempel på en andragradsekvation. Du kan se Action Script-koden.
PhET
En idé kan vara att ta en screenshot på en projektilbana från PhET-simuleringen ovan och klistra in i GeoGebra. Sedan sätter man tre eller fler punkter på kurvan och anpassar till en andragradsekvation. Det visar om inte annat bakvägen att fysiken innehåller andragradsfunktioner. Om man är osäker på hur man anpassar punkter till en funktion så har jag gjort det med mätvärdena från laborationen på tyngdacceleration.
Ekvationslösning med faktorisering
Måndagslektionen kommer att vigas åt utvärderingsåterkoppling och jag hinner blott gå igenom lösningen till Diagnosen.
Diagnosen blir läxa att göra om hemma och denna gång ska den ha alla rätt. Det gäller alla. Facit kommer upp på tisdag så kan alla rätta själva.
På tisdag som är en lång lektion kommer vi att göra uppdelning i faktorer både med konjugatregeln och kvadreringsreglerna om det går.
Uppdelning i faktorer med konjugatregeln
Först ska vi repetera konjugatregeln med ett lösblad där det är rad snabba uppgifter. Dessa uppgifter bör klaras av på mindre än tre minuter.
Vi kör samma övning som i måndags ävan idag.
Avsluta med att ge nästa lösblad som läxa .
Uppdelning i faktorer med kvadreringsreglerna
Här ska vi också repetera kvadreringsreglerna med ett lösblad.
Faktorisering och ekvationer
Onsdag
Repetera lösbladet från förra lektionen en gång till. I övrigt struntar vi i beting på faktorisering med kvadreringsregelerna.
Dagens beting: 1426-1430
Dataövning - konsekutiva tal
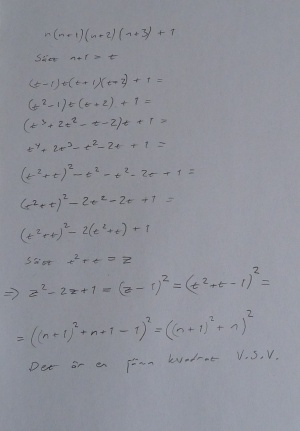
Del ett (n-1)(n+1)+1
Del två
Del tv är svårare. Det handlar om fyra konsekutiva tal. Addera ett till produkten av de fyra talen och ta roten ur. Detta ska bli ett heltal.
- Wolfram|Alpha har en lösning men ingen förklaring.
- Med hjälp av den ledtråden från Wolfram ser min lösning ut så här.
- Tanja löser uppgiften genom att pröva.
- Fredrik använder kvadratkomplettering och substitution för att lösa uppgiften. Lösningen syns i bilden till höger.
- Charlie i NV11 löser det genom att hitta mönster i de tal han prövar med och ...
Prov tisdag vecka 7
Diagnos 14
Repetition på fredag och måndag
Uppgift: Khan Academy
- Khan om hur man multiplicerar binom ska du verkligen öva på.
- Lös dessa Khan, relativt enkla andragradsekvationer. De kan lösas genom att gissa eller faktorisera.
Uppgifter
- Läs sammanfattningen på sidan 54.
- Gör Test 1 på sidan 55.
pappersövningar
- Öva ekvationer (= Extrablad ekvationer): finns bara på papper
- Faktorisering: finns bara på papper
- Öva konjugatregeln
- Öva kvadreringsreglerna
- Öva enkla andragradsekvationer: finns bara på papper
- Öva pq-formeln Senaste tillskottet
Provet skall vara tisdag vecka 7 (ligger på SchoolSoft).
Omprovet
Vi räknar klart det gamla provet (åtminstone E-uppgifterna) på extramatten och i slutet av lektionen gör vi ett förenklat prov med E-del för sig och C/A-del för sig.
Så får vi se hur det går.