Trigonometri Ma3C
Lektion 1 - Algebra repetition
| Uppgift |
|---|
| Repetitionstest
Skriv formler eller algebraiska förklaringar för detta:
|
Lektion 2
Trigonometri grundläggande
Andra länkar om trigonometri
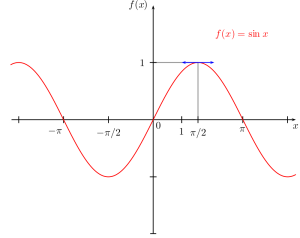
- Läs mer om sinus på Wikipedia.
- Engelska Wikipedia är ännu bättre på sinus.
- http://www.walter-fendt.de/m14e/sincostan_e.htm Walter Fendt om trigonometri
- Detta svar får du om du skriver in sine på Wolfram Alpha
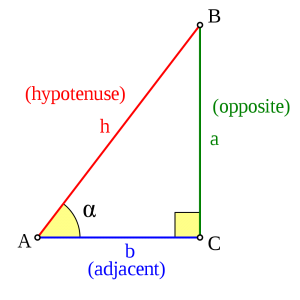
Definitioner:
- Motstående katet
- Närliggande katet
- Sin v = motstående katet / hypotenusan
- Cos v = närliggande katet / hypotenusan
- Tangens v = motstående katet / närliggande katet
Digitalt
- Grader och radianer
- Miniräknare eller dator
- Datorns räknare
- Excel - så här kan det se ut
Definition: Ta reda på vinkeln
Om y = roten ur x så är 'y2 = x. Dessa två hänger ihop och den ena kan ses som den omvända av den andre. Detta kallas inversen, den inversa funktionen.
På samma sätt som det finns en invers funktion till kvadraten på ett tal, nämligen roten ur så finns det en invers funktion till sinus och cosinus.
Om sin v = a/h då är v = arcsin(a/h) eller sin-1(a/h) Om cos v = b/h då är v = arccos(b/h) eller cos-1(b/h) 0ch på samma sätt för tangens
Den rätvinkliga triangeln
En rätvinklig triangel är en triangel där en av vinklarna är 90 grader. Sidan som är motsatt den räta vinkeln kallas hypotenusa och de två övriga sidorna kallas katetrar.
Om ytterligare en vinkel är känd i en rätvinklig triangel är även den tredje vinkeln känd då en triangels vinkelsumma är 180 grader. Trianglar som har samma uppsättning av vinklar är likformighet|likformiga. Detta innebär att om man känner till en vinkel i en rätvinklig triangel är även kvoten mellan sidorna känd. Dessa kvoter ges av de trigonometriska funktionerna för en vinkel A, där a, b och c syftar på sidorna i triangeln i bilden till höger enligt:
- Sinusfunktionens värde för en vinkel är kvoten mellan motsatta sidan till vinkeln och hypotenusan:
- [math]\displaystyle{ \sin A = \frac{a}{c} }[/math]
- Kosingsfunktionens värde för en vinkel är kvoten mellan närliggande sidan till vinkeln och hypotenusan:
- [math]\displaystyle{ \cos A = \frac{b}{c} }[/math]
- Tangensfunktionens värde för en vinkel är kvoten mellan motstående och närliggande sidas längd:
- [math]\displaystyle{ \tan A = \frac{a}{b} = \frac{\sin A}{\cos A} }[/math]
Med dessa funktioner är det möjligt att (givet exempelvis en sida och en vinkel) bestämma alla sidor och vinklar i en rätvinklig triangel.
Texten i ovanstående avsnitt kommer från Wikipedia.se
Lektion 3 - Fasta värden
En halv kvadrat
- [math]\displaystyle{ \sin 45 = \frac{1}{\sqrt{2}} }[/math]
-
- [math]\displaystyle{ \cos 45 = \frac{1}{\sqrt{2}} }[/math]
En halv liksidig triangel
- [math]\displaystyle{ \sin 60 = \frac{\sqrt{3}}{2} = \cos 30 }[/math]
-
- [math]\displaystyle{ \sin 30 = \frac{1}{2} = \cos 60 }[/math]
-
- [math]\displaystyle{ \tan 30 = \frac{1}{\sqrt{3}} }[/math]
-
- [math]\displaystyle{ \tan 60 = {\sqrt{3} }[/math]
Lektion 4 - Enhetscirkeln
Det handlar om trigonometri och cirklar.
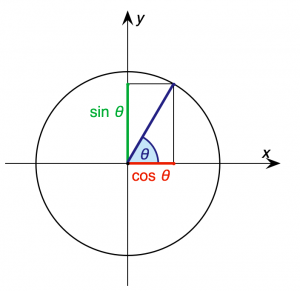
En enhetscirkel är en cirkel i planet med radie 1. Ofta talar man om enhetscirkeln och avser då en enhetscirkel med mittpunkt i origo. Av Pythagoras sats följer att enhetscirkeln kan beskrivas i kartesiska koordinater som mängden av punkter (x, y) sådana att x2 + y2 = 1. I polära koordinater blir detta den trigonometriska ettan.
För att beräkna de kartesiska koordinaterna (x, y) för en punkt på enhetscirkeln som befinner sig vid vinkeln t mätt från x-axeln kan man använda cosinus och sinus:
- [math]\displaystyle{ x = \cos t \qquad y = \sin t }[/math]
Texten i ovanstående avsnitt kommer från Wikipedia.se
Geogebra
Viktiga samband
<ggb_applet width="494" height="351" version="4.0" ggbBase64="UEsDBBQACAAIAKRtJEEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAKRtJEEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Rrbcts29jn9CgwfOslOJOFCgGQqpePE7WxmnKaz9u509mUHIiEZNUWyJCVLnj7sJ236Cf2A9Jf2ACAl6mLHl6Ru67EDEDg49xvBDL9ezlK0UGWl82zkkT72kMriPNHZdOTN60kv9L5++cVwqvKpGpcSTfJyJuuR5xtInYw8xcREjUPZwwzTni8j0YtwzHskFBFn4ZjyMPYQWlb6RZZ/J2eqKmSsTuNzNZMneSxrS/i8rosXg8Hl5WW/JdXPy+lgOh33l1XiIWAzq0ZeM3kB6LYOXTILTjEmgx/enjj0PZ1Vtcxi5SEjwly//OLJ8FJnSX6JLnVSn4+8MCQeOld6em5kEvAwMEAFKKRQca0XqoKjnUcrcz0rPAsmM7P/xM1QuhbHQ4le6ESVIw/3CWEcBywIoiDiIhSBh/JSq6xugFuigxbdcKHVpcNrZpak76E6z9OxNCjRzz8jiilGz81A3EBhEMJtYbeGmRuoG3w3cAfju+O+A/UdjO9gfOahha70OFUjbyLTClSos0kJ5ls/V/UqVZafZmEjPnkOMlX6CoAZBj9xOod1jJ+bPwF/vtkYbAtJOlTrcn5Hoi1JP/JvT5I+SFDW0iSHxKT8GjHFDUSd3LeRk/AOTSBlf+3fHkV2k5i7FN3zwwgK/3cRcThoQ2XYRAeqzg1s4z21mlUmXliEeGTcniAOsSEC8HKOSARDQBFEAyIc+RweSYiEGQPEAtjwEUMhMnCEIRscPIR//MAiE4gDMrMaQEwiAoR8xBkiNqZ8BJGEbFxCjFIGEJwjDocMeUINCiaQL+CJhcgHHk1IBgQAGRyEZyBPESOImcMkQFQgYfAR34S6CA3rgJIigZEgBiFENUS0i2aADxEz0ohGXTor5vWWiuJZ0k7rvFjbAqAhH23SnstPW1nxyTCVY5VCoTg1lkRoIVMTEZbQJM9q1BqRurVpKYtzHVenqq7hVIV+lAt5Imu1/Bagq5a2hY3zrPq+zOvXeTqfZRVCcZ7iNc95SjpzuuYaHlhnw+9u8M6G6MyDg3Rz2EHzSgH9vKxacJkkbwzEJjWAJt9l6epVqeRFkettMYYDW3OGah6nOtEy+xc4q6Fi9ILaEmTTVVuCGGUtI3mZnK4q8GC0/Lcqc0hVEe3jzg/E9MrtkID2/ZCsfzlwFksTeoTAjoigAoWYwoTC1uqavYayWqwNJJdqLfu0NHHdyG0e3lSv8nSzZKV/LYt6XtreAVJjaWQ6yqapsh5i4xoKc3wxzpenzjWYw3W2KuAJOwbGU6t1BJmBcuB32oxjN1oYw9kaClsYbCFw62s6We+TiFoIO47daKHAeR1rjaSkFZPgloyubD7D3lbUWM83ZX6e6fqkfah1fLGR1MB/N5+N1dp/tlGST4RyONjxr+GFKjOVNu4Mlpzn88pFZ8fTExXrGTy6jUYh0hjrn8CAW03UtFQt36ntypy67C7ueureskX1bZnP3mSLM/CEHQaGg5bLYRWXujAOh8ZQAi7UxqcSXUmoIEn3nIk/ED02lQLUUxvVQGTO6/O8tI0XJBQYLeRsJrMEZbbovMlqUBtkL2+TCCWklOURGAQQQEZZ2anlPp/XLcCRY7fBZsI5VTPo3lBtndb6/dp8Rxa7sRPKxz8CtR3zbvwAttcOaqrl1A1jN8i0OJemeWy0mcqVKrf0axG+zZMDxqjQ0h1Fq5HXs5Mr19u75tZwbOJvK2O71R0zgm85YT8i9qt7id2NWxvh95VaZuDK1iEgXxYuVAqlXJA5fmFSADqbmrbyfasv0ujrU6lr2/te6zJO1Y7rHTm3e7XncvHNLgchoOO1buOP6L4j7XXKx/dX/SaF1lDbL+AFprJNdd1kdDv5u04SZfs6V2H0VGUL4BRKK7wZ4lb5uNV+u7Ikrf+uSLN0RTqmAaOXeomOWvijFuoIeoKem7EG6ZHf4jriHTnVT5ljv3JZ1jQ4eqLjm835VpdlXh425zVZ5EtZ5NVXd8olzZE/Wkb5PAklm89U2XHrhZUbTs6b83zN+kPyTNfVyS010cBVqXmjRzOdWTQzCTphwiAcV9Cm1uo0hmqZbS41HGtNmwcvhNalwRqiUaSbTPSyU/KgiukrqNpyS5r7RNktkiI+lBS3TLQsSqBlkDQaPvYQLI68p3FePV2gv6Hf/osG8NaEnz2Hdj/bXnrmbTv24CMef/y4ZaTr6sKnQRgIHIlQcGZadOv5gRDYhx9GSBgF4WeoFKdqatYP55bjvbwib84oVYOt1aB81GKxUXDvgCpXh/V+1SV0n2qzk+H1rEh1rOu1KlMTAOv2EHx9v1m+UKow7yjvsrNSZpW5BHUwnSb8U5eK/5B7FAs49FctF7dQ6/FNaj2+ewU+fkAF/gxZqbcXHuxwWiK/X15au53LTxsdb2ep2+h+L1fdSvuPl7FI+361b5Q/ec46bOvWuNdUovHdrDv+g9iV9AnBlDJzBUY54YJ/0zMX9CuzRUPOA05JxAKGg5Bby4LFo9APcRBwhgmlOCR/Wkvb27kdO79yFjY1il4f0h/e32xve/+ztiZA77TztE9FGNEQ04BHVICmH9Lc2+8vd2rv300mlaqNB/DmoqS9p97xmL27wju04GW8SbtBe3WZpvnlP9QkVUur/U9oqn0j/XInI/2yayTcDwMqhImMKAqI8IP7Gam9x72/kXphYyX2WY3E8MOMdCLP1A87RgK1Wis13xDolpI2tjpTy/ojLV8NIGtNO/jHTKK6suJu66b59lPBy/xk853E3vZjr81y7Yt8Lcv6e9OHIGtj2scRY9jHgvgBjghp2hvIsxH3o8jnhHDKu93NHU3x/tamoHc0Bf3LmQLqXeRHHAsM1Y+2nWaEhYh4xEJOIzDRdbbYvzkwSmLN7cGXP83z+qtTnaGnJMS//q/34f0zNDIXCOjDe7fp7V8W7OmcParOd1QGuYwyf6MeErVdBIH0F0CFi4KI+CwQ1+ls0P22YT8fNv8V5uX/AVBLBwii0U0kuQgAAKcjAABQSwECFAAUAAgACACkbSRB1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAKRtJEGi0U0kuQgAAKcjAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAUAkAAAAA" showResetIcon = "false" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
- [math]\displaystyle{ x = \sin (180-t = \sin t }[/math]
- [math]\displaystyle{ \cos (- t) = \cos t }[/math]
Dagens mentala kliv
- De trigonometriska funktionerna fungerar för vinklar som är större än 90o. De gäller inom hela enhetscirkeln.
- Cos t = x-koordinaten och sin t = y-koordinaten.
- Även det omvända gäller. Enhetscirkeln kan hjälpa oss förstå de inversa funktionen sin-1 och cos-1 som att man utgår får ett värde på axeln, går ut till cirkeln och mäter den motsvarande vinkeln.
Trigonometriska ekvationer
Det trigonometriska ekvationerna har ofta flera lösningar.
Fördjupning: Här är en lösning till ekvationen sin v = o.5 i Wolfram Alpha. Den visar två lösningar till ekvationen (samt fler om man går ytterligare varv runt enhetscirkeln).
Övrigt
Konstigt facit: Bry er inte om bilden i facit till 1301.
Lektion 5 - Triangelsatserna
Grader och radianer
360 grader motsvarar 2 pi radianer.
Här finns material att hämta... http://en.wikipedia.org/wiki/Trigonometry
Areasatsen
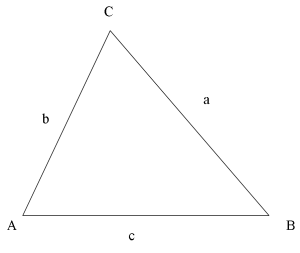[math]\displaystyle{ \mbox{Area} = \frac{1}{2}a b\sin C. }[/math]
Härledning
Triangeln borde ritas om så att sidan b är bas och horisontell.
Dra en höjd mot triangelns bas (sidan AC i detta fall).
- Höjden h = a sin C
- Triangelns area A = basen * höjden / 2
- Sätt in uttrycket för h ger:
- Arean = 1/2 ab sin C
Lektion 6 Sinussatsen
[math]\displaystyle{ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} }[/math]
Härledning
- Ställ upp areasatsenför alla tre vinklar.
- Förläng med 2.
- Dividera med abc
Lektion 7 Cosinussatsen
[math]\displaystyle{ c^2=a^2+b^2-2ab\cos C ,\, }[/math]
Härledning
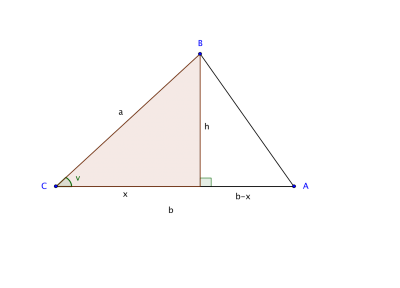
- Rita in en höjd i den vänstra triangeln så att det bildas två trianglar som i den högra bilden ovan.
- Använd Pythagoras för de båda trianglarna
- x2+h2 = c2 (1)
- (x-b)2+h2 = c2
- Förnkla uttrycket ger
- x2+b2-2bx+h2 = c2
- Stuva om i termerna
- x2+h2 = 2bx + c2-b2 (2)
- Sätt x2 + h2 lika. Ekvation (1) i ekvation (2)
- a2 = c2-b2+2bx
- Använd att x = acosC ger
- a2 = c2-b2+2bacosC
- Stuva om så att c2 står fritt ger
- c2 = a2+b2-2abcosC
Lektion 8 Problemlösning
Vad bör man tänka på vid problemlösning?
- Rta Figur
- Sätt ut variabler i figuren
- Välj Formel (eller sats)
- Utför beräkningarna
- Kontrollera om svaret är rimligt och om det finns flera svar
| Uppgift |
|---|
| Grupparbete
Denna lektion ska vi jobba med problemlösning i grupp. Ni väljer ett av problemen i boken och löser det tillsammans. Lösningen sk gå att presentera med projektor och ska lämnas in. Vem som helst i grupen ska kunna presentera den. Era lösningar kommer att publiceras på Wikiskola. Ni får 20 minuter på er. |
Lektion 9 Cirkelns ekvation
- Läs första sidan
- Koden ovan anropar en funktion som heter circle och som finns i ett bibliotek på sajten spelprogrammering.nu. Undersök hur funktionen ser ut.
- Ritas cirkeln på så sätt som i matteboken?
- * En cirkelbåge som går 360 grader är praktiskt. Det kallas polära koordinater.
- Kan vi gå tillväga som i funktionen för triangeln och skapa en cirkel med vår formel från matteboken?
Testa funktionen i GGB.