Andragradsfunktioner
Teori
Andragradsekvationer och rötter
| Exempel |
|---|
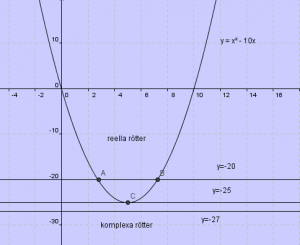
Lös ekvationen:
Vad händer? Pröva nu ekvationen:
här har vi en ekvation som saknar reella lösningar. |
| Definition |
|---|
En andragradsekvation kan ha två reella rötter eller en dubbelrot eller två komplexa rötter |
| Uppgift |
|---|
|
Fyra sätt att beskriva andragradaren
Vi kommer att arbeta med fyra representationer, fyra sätt att beskriva andragradsfunktionen. Alla sätt beskrivs mer ingående senare men här kommer en snabb sammanställning i några rader och eventuell bild.
Generell algebraisk form
Andragradsfunktionen på allmänn form [math]\displaystyle{ f(x) = ax^2 + bx + c }[/math].
Exempel: Andragradsfunktionen [math]\displaystyle{ f(x) = 2x^2 - 4 }[/math].
Vertex och nollställe
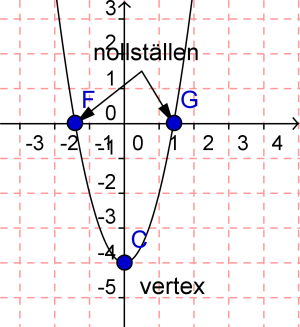
Varje parabel har en extrempunkt där den antar sitt högsta eller lägsta värde. Dessutom kan den ha ett eller två nollställen men det är inte alltid så.
Fokus och styrlinje
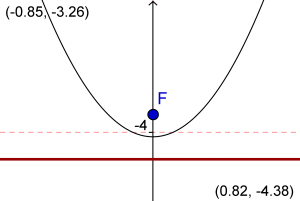
Andragradsfunktionen beskrivs och ritas upp utifrån en linje och en punkt.
Värdetabell
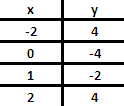
Som med alla funktioner kan man göra en värdetabell med x- och y-värden. När dessa talpar ritas in i ett koordinatsystem får man funktionens graf.
Kvadratiska modeller
Aktivitet
| Uppgift |
|---|
| xxx'
|
Lär mer
|
|
|
|
|
|
Kortdiagnos 4

