Geometriska satser och bevis ma1c

Från Wikiskola
Hoppa till navigering Hoppa till sök
Mål för undervisningen Potenser

I denna lektion definierar vi viktiga begrepp och presenterar några användbara satser som gäller vinklar.

Du kommer att ha nytta av detta vid problemlösning och kommande områden i matematiken.

Swayen till detta avsnitt: Vinklar


läromedel: Vinklar och sträckor


Läs om [ Vinklar saknas här]


Teori

Det finns en del definitioner och satser som gäller vinklar och vinkelsummor. De är nödvändiga att känna till vid problemlösning och de underlättar vid kommunikation om matematik.


Definition
{{{1}}}


Sats


Några viktiga satser om vinklar mm
Supplementvinklar
Supplementvinklar
Supplementvinklar är vinklar vars summa är π radianer eller 180°. Sidovinklar är ett annat ord för supplementvinklar.
Vinklarna behöver inte vara intilliggande. De kan till exempel vara hörn i en parallellogram. 



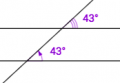Två linjer är parallella om de likbenägna vinklarna är lika stora.



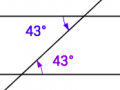Två linjer är paralella om alternatvinklarna är lika stora. Alternatvinklar definieras i figuren till höger.

 Vinkelsumman i en triangel är 180o



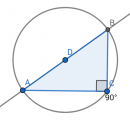Thales sats säger att om en sida i en triangel ligger längs en cirkels diameter, och om det tredje hörnet också ligger på cirkeln, så är vinkeln vid det tredje hörnet en rät vinkel.


Det mesta av informationen ovan kommer från Wikipedia.

Vinkelsumma

En linje som dras genom ett av triangelns hörn och är parallell med motstående sida, visar att triangelns vinkelsumma är 180 grader.


Bevis - vinkelsumman i en triangel

Testa först.

Geogebra Undersök med Geogebra-applet:

Triangelns vinkelsumma är 180 o

Flytta hörnen och se hur vinklarna ändras

Vad händer med vinkelsuman?

GGB från Liber.


Radianer

En vinkel eller ett vinkelområde är ett område av ett plan begränsat av två strålar, det vill säga delar av räta linjer som skär varandra i en punkt. Strålarna utgör vinkelområdets rand, och kallas för vinkelns ben. Skärningspunkten (och ändpunkten för strålarna) kallas för vinkelspets. Normalt markeras en vinkel med en vinkelbåge. Vinkelbegreppet används inom trigonometri och geometri.

För att mäta vinklar ritas en cirkelbåge med centrum i vinkelspetsen. Radianmåttet för vinkeln är längden av bågen mellan vinkelbenen dividerad med cirkelns radie. Vanligen uttrycks dock vinkeln i grader.

[math]\displaystyle{ \theta(rad) = \frac{b{a\!\!^\circ}gl{\ddot a}ngden}{radien} }[/math]
[math]\displaystyle{ \theta(grader) = \frac{b{a\!\!^\circ}gl{\ddot a}ngden}{omkretsen}\cdot 360 }[/math]

Symbolen för enheten grad är en lite upphöjd cirkel (°).

Aktiviteter

Övning: Titta på alla filmer om vinklar på Geogebra

Övning 2

Beskriv vinklarna i figuren med lämpliga begrepp, exempelvis likabelägna vinklar, alternatvinklar, mm.

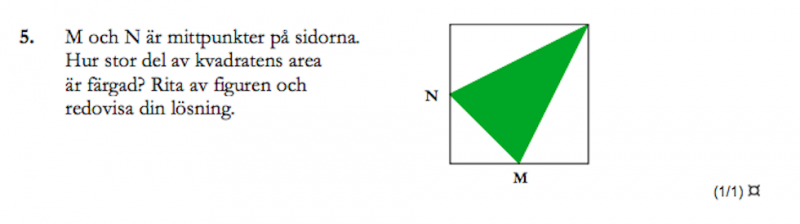
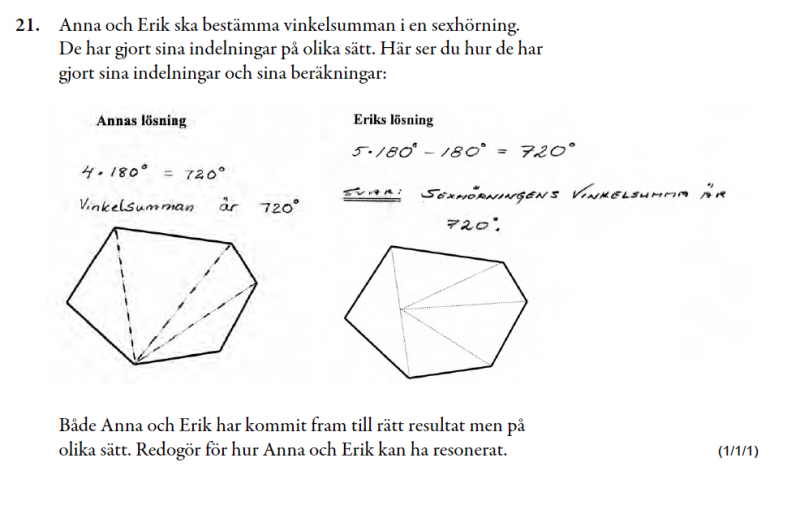
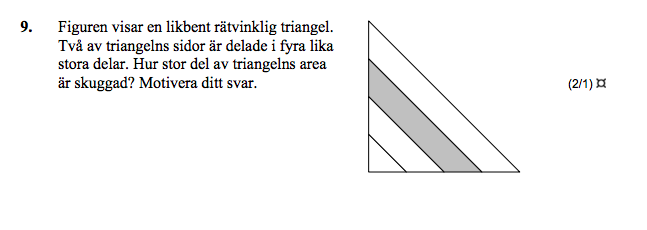
Lös uppgifterna nedan

Det är tre uppgifter från olika nationella prov (före Gy11). Provåret framgår av bildens namn.

Lär mer

Mycket av informationen ovan kommer från Wikipedia:

Euklides elementa 8Wikipedia)
Elementa på Projekt Runeberg

Exit ticket

Hämtad från ”https://wikiskola.se/index.php?title=Geometriska_satser_och_bevis_ma1c&oldid=41505”