Rörelse och krafter
CI-delar
- Tvådimensionell rörelse i gravitationsfält och elektriska fält.
- Centralrörelse.
- Vridmoment för att beskriva jämviktstillstånd.
- Simulering av tvådimensionell rörelse med hjälp av enkla numeriska metoder.
Inroducera kurs + Kap 1 s 8-10
Vridmoment
Se filmen hemma och svara på frågan, nedan. En hemlig länk
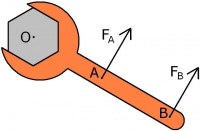
Kraftmoment eller vridmoment
| Uppgift |
|---|
Väg med et besman
.png) Ett besman enligt figuren består av en en meter lång stång med en centimeterskala. I stångens ena ände hänger man det man det föremål som ska vägas och i den andra änden sitter en 1.5 kg tung metallklump. Skalan visar att den korta delen är 37 cm. Vad väger föremålet. |
Ta med: balansvåg med vikter, linjal och tyngder.
v 41
neXus Fysik A sid 68: Tyngdkraftens komposanter på ett sluttande plan.
neXus FYSIK A: Sidorna 70-74.
Förra gången: Men kanske först något om tyngdkraften (och dess komposanter) när en bok exempelvis ligger på ett lutande plan och jämvikt råder mellan tyngdkrafter och friktionskraften.
Kraftmoment
M = F * l F är kraften, l är det vinkelräta avståndet mellan kraften och rotationscentrum l kan ses som avståndet till kraftens angreppspunkt men då får man räkna med den vinkelräta komposanten
Teori: Wikipedia om Kraftmoment. OBS! Wikipedia använder begreppet vridmoment med bokstaven τ istället.
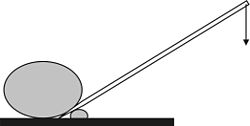
Wikipedia om hävstången.
Demo: Walter Fendt - The Lever
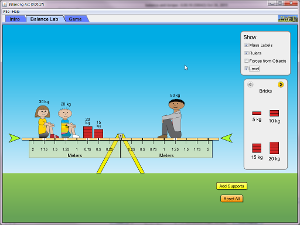
Demo: Riktig balansvåg...
Övningsuppgift från Provbanken NP Fysik A vt-2005
Facit: (klicka expandera till höger)
Kap 2 s 16-17 - Jämvikt
Flipp
- Räkna så många uppgifter du hinner hemma.
- Titta på filmen och svara på frågorna
- OBS! Vi var några stycken som undrade över uppgift 2.4b. Lösning finns här: Det är Andreas Josefsson, Tullängsskolan Örebro som gjort de fina lösningarna
Jämvikt
Om summan av alla krafter samt kraftmoment som verkar på ett föremål är noll då är föremålet i jämvikt.
Wikipedia har en bra bild på kraftjämvikt för kloss på lutande plan.
| Click to Run |
Uppgift vridmoment
| Uppgift |
|---|
| Extra inlämningsuppgift - Nagelklipparen
Vilken utväxling får man med denna nagelklippare? Totala längden är cirka 7 cm. Redovisa dina beräkningar. Använd figuren och sätt ut relevanta mått och krafter. Redovisa uppgiften i en pdf som mejlas in.  |
Kap 3 s 26-33
Frågor
Rörelser kan sammansättas och uppdelas
Rörelser kan studeras i koordinatsystem
Repetition - formler från Fysik 1
Sträcka
s = v0t + at2 / 2
Hastighet
Vid en konstant acceleration a, gäller att:
v = v0 + at
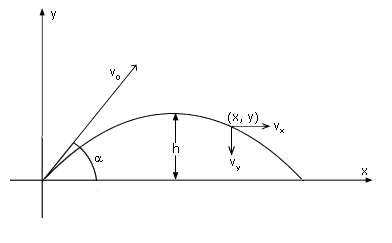
Kaströrelse
Detta avsnitt är hämtat från WikiBooks Formelsamling i Fysik.
|
[math]\displaystyle{ \left\{\begin{matrix} v_x = v_0 \cos \alpha \\ v_y = v_0 \sin \alpha -gt \end{matrix}\right. }[/math] |
|
| [math]\displaystyle{ \left\{\begin{matrix} x = v_0 t \cos \alpha \\ y = v_0 t \sin \alpha -\frac {1}{2}gt^2 \end{matrix}\right. }[/math] | |
| [math]\displaystyle{ h = \frac{v_0^2}{2g}(\sin \alpha)^2 }[/math] |
Kaströrelse i GeoGebra
Velocity Components i Projectile Motion
Simulering av kaströrelse
från PhET och Wikipedia: Trajectory_of_a_projectile
Raäkneövning
Kap 3 s34-38
Kaströrelse i elektriska fält
Matematisk rörelsebeskrivning
Kap 3 s 39-45
Kroklinjig rörelse
Kraftekvationen på vektorform
Kap 3 s 46-52
Övningar i boken: 3.1-3.30.