Numerisk lösning av integraler: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Hakan (diskussion | bidrag) (Skapade sidan med '{{Lm4|Numerisk|164-169}} === Numerisk lösning av integraler === {{#ev:youtube | IcecyaONFwI | 340 | right | Trapetsmetoden för lösning av integraler. Av Tomas Severin, You...') |
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
||
| Rad 1: | Rad 1: | ||
{{Lm4|Numerisk|164-169}} | {{Lm4|Numerisk|164-169}} | ||
=== Numerisk lösning av integraler === | ===Numerisk lösning av integraler=== | ||
{{#ev:youtube | IcecyaONFwI | 340 | right | Trapetsmetoden för lösning av integraler. Av Tomas Severin, Youtubelicens.}} | {{#ev:youtube | IcecyaONFwI | 340 | right | Trapetsmetoden för lösning av integraler. Av Tomas Severin, Youtubelicens.}} | ||
| Rad 12: | Rad 12: | ||
{{clear}} | {{clear}} | ||
=== Hemuppgift trapetsmetoden=== | ===Hemuppgift trapetsmetoden=== | ||
{{uppgfacit | En NP-uppgift med trapetsmetoden | {{uppgfacit | En NP-uppgift med trapetsmetoden | ||
| Rad 28: | Rad 28: | ||
}} | }} | ||
=== Prova en svårlöslig integral med digitala verktyg === | ===Prova en svårlöslig integral med digitala verktyg=== | ||
Kan du lösa denna integral analytiskt? | Kan du lösa denna integral analytiskt? | ||
| Rad 40: | Rad 40: | ||
Läs mer [http://reference.wolfram.com/language/tutorial/IntegralsThatCanAndCannotBeDone.html här]. | Läs mer [http://reference.wolfram.com/language/tutorial/IntegralsThatCanAndCannotBeDone.html här]. | ||
=== Formativ lektionskontroll === | ===Formativ lektionskontroll=== | ||
[[Fil:NP E 1996 Integraluppgift med bromssträcka.png|340px|miniatyr|höger|Alla gör denna uppgift för hand så jag kan se att de förstår detta.]] | [[Fil:NP E 1996 Integraluppgift med bromssträcka.png|340px|miniatyr|höger|Alla gör denna uppgift för hand så jag kan se att de förstår detta.]] | ||
* Om allt gått väl kan alla nu lösa denna uppgift. I så fall kan vi gå vidare. | *Om allt gått väl kan alla nu lösa denna uppgift. I så fall kan vi gå vidare. | ||
* Om det är många som inte kan detta måste vi repetera. Vi måste också diskutera, utvärdera och komma överens om hur vi ska göra för att lära oss detta. | *Om det är många som inte kan detta måste vi repetera. Vi måste också diskutera, utvärdera och komma överens om hur vi ska göra för att lära oss detta. | ||
* Om de flesta men inte alla kan detta kommer vi att gå vidare i klassen. De som ännu inte klarar detta får diskutera med mig hur de kan göra för att komma vidare. | *Om de flesta men inte alla kan detta kommer vi att gå vidare i klassen. De som ännu inte klarar detta får diskutera med mig hur de kan göra för att komma vidare. | ||
[[Lösningsförslag till NP E 1996 Integraluppgift]] | [[Lösningsförslag till NP E 1996 Integraluppgift]] | ||
<br /> | |||
{{clear}} | {{clear}} | ||
== Programmeringsövning == | |||
[[Jämföra integraler numeriskt]] | |||
<br /> | |||
Nuvarande version från 10 augusti 2021 kl. 12.34
Numerisk lösning av integraler
Läs vad Wikipedia skriver om Trapetsmetoden
Hemuppgift trapetsmetoden
Facit: (klicka expandera till höger)
Läs inte den här ledtråden förrän du har försökt själv med uppgiften. Lösningsförslaget i den länakde sidan är en GeoGebra som ska vara underlag för en diskussion på lektionen. Lösningsförslag till NP-uppgift fr vt 1999
Prova en svårlöslig integral med digitala verktyg
Kan du lösa denna integral analytiskt?
[math]\displaystyle{ \int {\sin(x^2)dx} }[/math]
Det är svårt att finna en primitiv funktion, eller hur?
Prova att lösa den med WolframAlpha och GeoGebra.
Läs mer här.
Formativ lektionskontroll
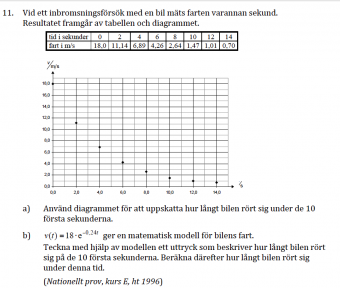
- Om allt gått väl kan alla nu lösa denna uppgift. I så fall kan vi gå vidare.
- Om det är många som inte kan detta måste vi repetera. Vi måste också diskutera, utvärdera och komma överens om hur vi ska göra för att lära oss detta.
- Om de flesta men inte alla kan detta kommer vi att gå vidare i klassen. De som ännu inte klarar detta får diskutera med mig hur de kan göra för att komma vidare.
Lösningsförslag till NP E 1996 Integraluppgift


