Tal och talmängder: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
||
| Rad 8: | Rad 8: | ||
Du ska lära dig vad som kännetecknar naturliga tal, heltal, rationella tal, reella tal och komplexa tal. }} | Du ska lära dig vad som kännetecknar naturliga tal, heltal, rationella tal, reella tal och komplexa tal. }} | ||
Exit ticket Länk | |||
{{clear}} | {{clear}} | ||
Versionen från 14 augusti 2017 kl. 14.14
Inledning
samt de positiva och negativa talen {…, −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, …}.
Mängden av heltalen betecknas ℤ (eller, av vissa typografiska skäl kan ett vanligt Z i fetstil användas), från det tyska ordet Zahlen (som betyder "tal").
Mängden av heltalen är uppräkneligt oändlig.
När det gäller datorsystem används termen heltal (de hela talen) som distinktion till flyttal (de reella talen) eftersom de i datorer hanteras, beräknas och lagras olika.
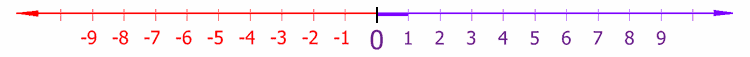
Rationella tal
Rationella tal, "bråktal", är de tal som kan skrivas som en kvot (ett bråk) av två heltal:
- [math]\displaystyle{ \frac{T}{N} }[/math]
där heltalet T är bråkets täljare och heltalet N bråkets nämnare.
Mängden av de rationella talen betecknas ℚ (eller, av vissa typografiska skäl kan ett vanligt Q i fetstil används).
Reella tal
Reella tal innefattar de tal som man vanligtvis menar med tal. De kan beskrivas som alla punkter på en kontinuerlig linje, utan att det finns glapp mellan talen i linjen. Denna linje brukar kallas den reella tallinjen.
Mängden av de reella talen betecknas ℝ (eller, av vissa typografiska skäl kan ett vanligt R i fetstil användas).
Öva själv
GGB inäddad
Läs mer
Stora delar av texten ovan har hämtats från Wikipedia: Wikipedia skriver om Tal


