Lektion 6 Sinussatsen: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
||
| Rad 1: | Rad 1: | ||
{{#ev:youtube|R1Sjs8FIu38|240|right|Sinussatse}} | {{#ev:youtube|R1Sjs8FIu38|240|right|Sinussatse}} | ||
{{#ev:youtube| wBTe_xo1G8E |240|right|Sinussatse, av Åke Dahllöf.}} | |||
[[Fil:Triangle_ABC_with_Sides_a_b_c.png|300px]] | [[Fil:Triangle_ABC_with_Sides_a_b_c.png|300px]] | ||
<math>\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} </math> | <math>\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} </math> | ||
Versionen från 9 september 2015 kl. 21.13
[math]\displaystyle{ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} }[/math]
Härledning 1
- Ställ upp areasatsenför alla tre vinklar.
- Förläng med 2.
- Dividera med abc
Härledning 2
Härledning
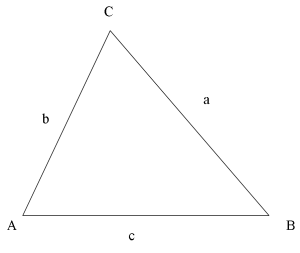
Antag en triangel med sidorna a, b och c och med de motstående vinklarna A, B och C. En linje med längden h och vinkelrät mot sidan c är dragen från hörnet C till motstående sida c eller sidan c:s förlängning.
Då är
- [math]\displaystyle{ \sin A = \frac{h}{b} }[/math]
och
- [math]\displaystyle{ \; \sin B = \frac{h}{a} }[/math]
Vilket är ekvivalent med
- [math]\displaystyle{ h = b\,\sin A = a\,\sin B }[/math]
och
- [math]\displaystyle{ \frac{\sin A}{a} = \frac{\sin B}{b} }[/math]
Om linjen dras mellan vinkeln A och sidan a och samma procedur upprepas blir resultatet
- [math]\displaystyle{ \frac{\sin B}{b} = \frac{\sin C}{c} }[/math]
