Rad 4:
Rad 4: [[Fil:1000px-Sinus.svg.png|thumb|left|CC Wikimedia.org]]
[[Fil:1000px-Sinus.svg.png|thumb|left|CC Wikimedia.org]]
<ggb_applet width="586" height="434" version="3.2" ggbBase64="UEsDBBQACAgIAJpbiT8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1Vndbts2FL5en4LQxdBujSOK+kXjFkkLDAWypViyYRhyQ8u0rUUSXZFy7Ra93JtsL7BX6P2eaYekfv2T2lnbZTeWxJ9D8nzf+c6RfPJsmaVowQqR8Hxo4YFtIZbHfJzk06FVyslRaD17+uBkyviUjQqKJrzIqBxaZOBYqr1Mnj746kTM+BtEUz3k54S9GVoTmgpmITEvGB2LGWOy107LZZImtFhdjH5jsRRthzHyMp+XsIosSmiLs/F5IurHY7VgSkcshT1eylXKEFrQFLZkuiY8lwiJ5C2D8/imLea5eFVw+ZynZZYLhGKe2o15nuLOvdO5J82+4MHtdHh1R888hx5UCgbL8ELUw5VzLvJ0dQauuJnzJG+PC7NPjrUPT1gZp8k4obnyk/YpnAChN8lYzoaWF/oWmrFkOgM3uMSp1+XF+HIlJMvQ8ldW8KHlBIPQDf0gdDAhdmSreSvTRWw8wJEf2bZPQmyTCLYW0xTc5AYDHLgYYwc7JApcD+bs7NIrs8UlkxIAEIguWQvftEjGvYeX4oynbZM+/nM6l2WhGUaqJo3j0AL2FeqMp/k0ZVUbBofPWHwz4stLAyoxpq9Wcz1Fb2g01U5HBbiAgJlpdR3B1as2rXbajDJjzIjKhjLa9OPI0SP0dWSuhnpJbrZWnRzXp8Z2vUwikGqwDfbN4TVph5aFyjyR5/WDTOKb9qhqwg9lNmINf/o28aeyeXK8xriTG1bkLK34DNiWvBQmsjpUH7M4yeDRdFQuoQqun2ADpnXMpgWrN27i2ThM99pd7q41nxzXm9AxBXuNJQgTnEeqs1wBOXjOMyaLBBUf/pCLJL9Jk+ljCPe8FPqCFugIfVfJlRIaOeMA5ysmWYE+/C7KzEJjKsGapbbxhhc3Wp6u2FIiOuIL1YPAj8rJhy+oDsFSljEQIakJmpcZK5K4gUqZYKleHA5e1scfeKFxjNZSrmWxVpBqZksH6G6JaldEtZ2G7iCj8xlVVnGtlys4ftf/2ubFZCKYREuFJFr1+77n4z5iAtgCRrIkV4aB3BldqkQAd3QkQFklu4wB+Pycx1TqfGK2X2mYY+tZak6obmA919bTJ8mStRoBeCVvgYG0d+Q27OQM2J0zIbR8yK4K0BzIqRkDmjjX21T8nzNlXie3ejiag0u0BHWUuALuoxAKyYuU3axj6A+iLw/hnjBh5y44+RVOxP/cON0NpphnGc3HKKcZDH+ZQ4wLcLoGJlElBKKQ5penoJ5weMjyK31rAChlPeDU2K2sbcCvM1QD4am1AXFfi7dj7LsaYnUZmUsDsH0YwFo5hcLHruA50jdvje/0GJNUVQXRlkY9fi+hMBOq6Kt3fQaF3xKgeFiR+zECo4+svgs21a3vm7O7+QY7nuG/um7w/87uUfGoVe1Q7/Rpdcmmqn2NVKeGUGcbZJreTiZRWas9MrV2Ro27FjW7ZaWToLt+7dc4+3q0TQpYu68uoj/m7qOajtrvb7sL7XM69jo3Y4QpXJJsniZxIhsHp0oImhgH6m5WJzeMzVVZeJFfFTQX6mXFjOlUPTtQviigUIBkT9Nz2O0a2GcG7OVW9RjdDrg6fAPUaDfazm1o7xNFd0P7NkBxBWgdQE2C2+sAtwF6uxa92NAiUzShb1DVcqgwvbiXwuQObJXxP5M0vdhg6mw155JB4UoP06jOvE8gVp+Sva1WHXmByYXY2woC3mB35f3/q2Dpd+TtOqUI4GwjwOJ23PV7XPuisuUdBQIgJEFEPA/72Mb/5RsLIRXe24MOH6BUtIg7IVd/LUjhFfBHNknZUrt6X1y2x+SLXeVCxqWQH/5k+ZgdFpTdifc2Kh1fg+TcilEbk21I1innyAkGPibhfY7LzQSmPibgKol9/brk8sn1pKDxuw5m79+1qvr++snwuhpihqNvUWcsPJnm9213O7vt1WbM/baUKGFXVn+LX44TG+kwEef0iv3SdyvsRtJCvlJZENVFpePbbkjsCAdh4DrY0wTxBpHjuAFxnSgCMYp6efQw1WxiU6vm6UaI/v3XIbIJo9d0Ew+8wA4inzh+ELlh5Pt3rOc/zXeCOyujc7Aybo8M0ouMhtEPu4w/7hD80V5kJnuTOeb5ODFfH9Sn+Wow/WxMX6M0GRDs28ACHBIvAD5UfCYBcQKP+A7BYejuonPfCyPOU0bz5pB0nXudwPrS0u+Ygqz+s2JHUUznGgndJha02I9CTo9C6ivs9RO0UD9D9QMN1y2xFo1CHiqQzv0XSIh7N/QcHJAIE9slvh9W7xa+a9tB4ESuH3pRGO0k1FYHuztiFDz7cPFov4h0/2VExv+xa8nA8UI3aoKyfmnzA1J72w1ClY/uEqrxfQpVU6aF/y5Uj7v/2eh/Nqt/RZ7+A1BLBwirGVuj9wYAAGceAABQSwECFAAUAAgICACaW4k/qxlbo/cGAABnHgAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAADEHAAAAAA==" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true" />
:
:
::::Peter Åsum har gjort ovanstående [http://www.geogebra.se/ma_a/trigonometri/sinv_ratvinklig_trigonometri_t.html GeoGebra om Sinus]
::::Peter Åsum har gjort ovanstående [http://www.geogebra.se/ma_a/trigonometri/sinv_ratvinklig_trigonometri_t.html GeoGebra om Sinus]
Versionen från 17 augusti 2015 kl. 13.23
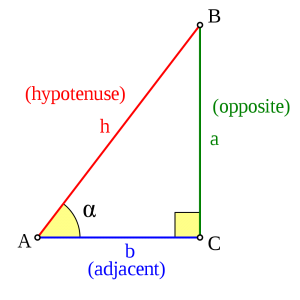
Trigonometri grundläggande CC By CC Wikimedia.org
Peter Åsum har gjort ovanstående GeoGebra om Sinus
Andra länkar om trigonometri
Definitioner:
Motstående katet
Närliggande katet
Sin v = motstående katet / hypotenusan
Cos v = närliggande katet / hypotenusan
Tangens v = motstående katet / närliggande katet Digitalt
Definition: Ta reda på vinkeln
Om y = roten ur x så är 'y2 = . Dessa två hänger ihop och den ena kan ses som den omvända av den andre. Detta kallas inversen, den inversa funktionen.
På samma sätt som det finns en invers funktion till kvadraten på ett tal, nämligen roten ur så finns det en invers funktion till sinus och cosinus.
Om sin v = a/h då är v = arcsin(a/h) eller sin-1 (a/h)
Om cos v = b/h då är v = arccos(b/h) eller cos-1 (b/h)
0ch på samma sätt för tangens