Trigonometri Ma3C: Skillnad mellan sidversioner

Från Wikiskola
Hoppa till navigering Hoppa till sök
VisuellWikitext
Rad 16: Rad 16:
}}
}}


== Lektion 2 ==
== [[Lektion 2 - Trigonometriska grunder]] ==
 
{{#ev:youtube| hB3PZPDPHy8 |240|left|}}{{#ev:youtube| Rl92xUAmhgI |240|right|}}
{{clear}}
{{#ev:youtube| _ALeqdwMxwM |240|right|}}
 
{{trigonometri grund}}
 
=== Den rätvinkliga triangeln ===
 
[[Fil:Rtriangle.png|höger|miniatyr|200px|En rätvinklig triangel med hypotenusan ''c'' och katetrarna ''a'' och ''b''.]]
En rätvinklig triangel är en triangel där en av vinklarna är 90 grader. Sidan som är motsatt den räta vinkeln kallas '''hypotenusa''' och de två övriga sidorna kallas '''katetrar'''.
 
Om ytterligare en vinkel är känd i en rätvinklig triangel är även den tredje vinkeln känd då en triangels vinkelsumma är 180 grader. Trianglar som har samma uppsättning av vinklar är likformighet|likformiga. Detta innebär att om man känner till en vinkel i en rätvinklig triangel är även kvoten mellan sidorna känd. Dessa kvoter ges av de trigonometriska funktionerna för en vinkel ''A'', där ''a'', ''b'' och ''c'' syftar på sidorna i triangeln i bilden till höger enligt:
 
* Sinusfunktionens värde för en vinkel är kvoten mellan motsatta sidan till vinkeln och hypotenusan:
::<math>\sin A = \frac{a}{c}</math>
* Kosingsfunktionens värde för en vinkel är kvoten mellan närliggande sidan till vinkeln och hypotenusan:
::<math>\cos A = \frac{b}{c}</math>
* Tangensfunktionens värde för en vinkel är kvoten mellan motstående och närliggande sidas längd:
::<math>\tan A = \frac{a}{b} = \frac{\sin A}{\cos A}</math>
 
Med dessa funktioner är det möjligt att (givet exempelvis en sida och en vinkel) bestämma alla sidor och vinklar i en rätvinklig triangel.
{{wp}}
 
 
{{khanruta|
* [http://www.khanacademy.org/math/trigonometry/e/trigonometry_0.5 trigonometry 0.5 - den rätvinkliga triangeln]
* [http://www.khanacademy.org/math/trigonometry/e/trigonometry_1.5 trigonometry 1.5 - den rätvinkliga triangeln]
* [http://www.khanacademy.org/math/trigonometry/e/trigonometry_2 trigonometry 2.0 - den rätvinkliga triangeln]
}}
 
{{lm3c|Trigonometri|10}}
:
{{Läxa|Lös uppgifterna 1201-1207 och gärna fler.
}}
{{flipp}}


== Lektion 3 - Fasta värden ==
== Lektion 3 - Fasta värden ==

Versionen från 17 augusti 2015 kl. 10.54

Lektion 1 - Algebra repetition

Uppgift
Repetitionstest

Skriv formler eller algebraiska förklaringar för detta:

  • kvadreringsreglerna
  • formelhantering: Vad är [math]\displaystyle{ R }[/math] om [math]\displaystyle{ I=\frac{U}{R} }[/math]
  • pq-formeln
  • Pythagoras sats


Läxa!

  • Räkna uppgifterna på sidan 9.
  • Titta även igenom innehållet till lektion 2 här på wikiskola.


Lektion 2 - Trigonometriska grunder

Lektion 3 - Fasta värden

Load video
YouTube

En halv kvadrat

[math]\displaystyle{ \sin 45 = \frac{1}{\sqrt{2}} }[/math]
[math]\displaystyle{ \cos 45 = \frac{1}{\sqrt{2}} }[/math]

En halv liksidig triangel

[math]\displaystyle{ \sin 60 = \frac{\sqrt{3}}{2} = \cos 30 }[/math]
[math]\displaystyle{ \sin 30 = \frac{1}{2} = \cos 60 }[/math]
[math]\displaystyle{ \tan 30 = \frac{1}{\sqrt{3}} }[/math]
[math]\displaystyle{ \tan 60 = {\sqrt{3} }[/math]


Öva på Khan: Special right triangles

Läxa! Lös uppgifterna 1218-1223 och gärna fler.

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!


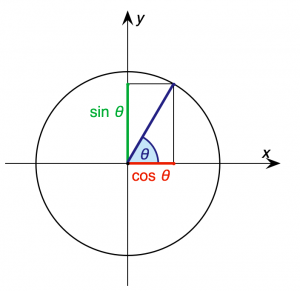
Lektion 4 - Enhetscirkeln

Load video
YouTube
Enhetscirkeln intro
Load video
YouTube
Enhetscirkeln del 2
Enhetscirkeln. Koordinaten för en punkt på cirkeln kan beräknas utifrån vinkeln t med hjälp av cosinus och sinus.
Enhetscirkeln. Koordinaten för en punkt på cirkeln kan beräknas utifrån vinkeln t med hjälp av cosinus och sinus.
Ma3C: Enhetscirkeln, sidan 16-21


Det handlar om trigonometri och cirklar.

En enhetscirkel är en cirkel i planet med radie 1. Ofta talar man om enhetscirkeln och avser då en enhetscirkel med mittpunkt i origo. Av Pythagoras sats följer att enhetscirkeln kan beskrivas i kartesiska koordinater som mängden av punkter (x, y) sådana att x2 + y2 = 1. I polära koordinater blir detta den trigonometriska ettan.

För att beräkna de kartesiska koordinaterna (x, y) för en punkt på enhetscirkeln som befinner sig vid vinkeln t mätt från x-axeln kan man använda cosinus och sinus:

[math]\displaystyle{ x = \cos t \qquad y = \sin t }[/math]

Texten i ovanstående avsnitt kommer från Wikipedia.se

Geogebra

Malin C om Enhetscirkeln.

Viktiga samband

<ggb_applet width="494" height="351" version="4.0" ggbBase64="UEsDBBQACAAIAKRtJEEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAKRtJEEAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Rrbcts29jn9CgwfOslOJOFCgGQqpePE7WxmnKaz9u509mUHIiEZNUWyJCVLnj7sJ236Cf2A9Jf2ACAl6mLHl6Ru67EDEDg49xvBDL9ezlK0UGWl82zkkT72kMriPNHZdOTN60kv9L5++cVwqvKpGpcSTfJyJuuR5xtInYw8xcREjUPZwwzTni8j0YtwzHskFBFn4ZjyMPYQWlb6RZZ/J2eqKmSsTuNzNZMneSxrS/i8rosXg8Hl5WW/JdXPy+lgOh33l1XiIWAzq0ZeM3kB6LYOXTILTjEmgx/enjj0PZ1Vtcxi5SEjwly//OLJ8FJnSX6JLnVSn4+8MCQeOld6em5kEvAwMEAFKKRQca0XqoKjnUcrcz0rPAsmM7P/xM1QuhbHQ4le6ESVIw/3CWEcBywIoiDiIhSBh/JSq6xugFuigxbdcKHVpcNrZpak76E6z9OxNCjRzz8jiilGz81A3EBhEMJtYbeGmRuoG3w3cAfju+O+A/UdjO9gfOahha70OFUjbyLTClSos0kJ5ls/V/UqVZafZmEjPnkOMlX6CoAZBj9xOod1jJ+bPwF/vtkYbAtJOlTrcn5Hoi1JP/JvT5I+SFDW0iSHxKT8GjHFDUSd3LeRk/AOTSBlf+3fHkV2k5i7FN3zwwgK/3cRcThoQ2XYRAeqzg1s4z21mlUmXliEeGTcniAOsSEC8HKOSARDQBFEAyIc+RweSYiEGQPEAtjwEUMhMnCEIRscPIR//MAiE4gDMrMaQEwiAoR8xBkiNqZ8BJGEbFxCjFIGEJwjDocMeUINCiaQL+CJhcgHHk1IBgQAGRyEZyBPESOImcMkQFQgYfAR34S6CA3rgJIigZEgBiFENUS0i2aADxEz0ohGXTor5vWWiuJZ0k7rvFjbAqAhH23SnstPW1nxyTCVY5VCoTg1lkRoIVMTEZbQJM9q1BqRurVpKYtzHVenqq7hVIV+lAt5Imu1/Bagq5a2hY3zrPq+zOvXeTqfZRVCcZ7iNc95SjpzuuYaHlhnw+9u8M6G6MyDg3Rz2EHzSgH9vKxacJkkbwzEJjWAJt9l6epVqeRFkettMYYDW3OGah6nOtEy+xc4q6Fi9ILaEmTTVVuCGGUtI3mZnK4q8GC0/Lcqc0hVEe3jzg/E9MrtkID2/ZCsfzlwFksTeoTAjoigAoWYwoTC1uqavYayWqwNJJdqLfu0NHHdyG0e3lSv8nSzZKV/LYt6XtreAVJjaWQ6yqapsh5i4xoKc3wxzpenzjWYw3W2KuAJOwbGU6t1BJmBcuB32oxjN1oYw9kaClsYbCFw62s6We+TiFoIO47daKHAeR1rjaSkFZPgloyubD7D3lbUWM83ZX6e6fqkfah1fLGR1MB/N5+N1dp/tlGST4RyONjxr+GFKjOVNu4Mlpzn88pFZ8fTExXrGTy6jUYh0hjrn8CAW03UtFQt36ntypy67C7ueureskX1bZnP3mSLM/CEHQaGg5bLYRWXujAOh8ZQAi7UxqcSXUmoIEn3nIk/ED02lQLUUxvVQGTO6/O8tI0XJBQYLeRsJrMEZbbovMlqUBtkL2+TCCWklOURGAQQQEZZ2anlPp/XLcCRY7fBZsI5VTPo3lBtndb6/dp8Rxa7sRPKxz8CtR3zbvwAttcOaqrl1A1jN8i0OJemeWy0mcqVKrf0axG+zZMDxqjQ0h1Fq5HXs5Mr19u75tZwbOJvK2O71R0zgm85YT8i9qt7id2NWxvh95VaZuDK1iEgXxYuVAqlXJA5fmFSADqbmrbyfasv0ujrU6lr2/te6zJO1Y7rHTm3e7XncvHNLgchoOO1buOP6L4j7XXKx/dX/SaF1lDbL+AFprJNdd1kdDv5u04SZfs6V2H0VGUL4BRKK7wZ4lb5uNV+u7Ikrf+uSLN0RTqmAaOXeomOWvijFuoIeoKem7EG6ZHf4jriHTnVT5ljv3JZ1jQ4eqLjm835VpdlXh425zVZ5EtZ5NVXd8olzZE/Wkb5PAklm89U2XHrhZUbTs6b83zN+kPyTNfVyS010cBVqXmjRzOdWTQzCTphwiAcV9Cm1uo0hmqZbS41HGtNmwcvhNalwRqiUaSbTPSyU/KgiukrqNpyS5r7RNktkiI+lBS3TLQsSqBlkDQaPvYQLI68p3FePV2gv6Hf/osG8NaEnz2Hdj/bXnrmbTv24CMef/y4ZaTr6sKnQRgIHIlQcGZadOv5gRDYhx9GSBgF4WeoFKdqatYP55bjvbwib84oVYOt1aB81GKxUXDvgCpXh/V+1SV0n2qzk+H1rEh1rOu1KlMTAOv2EHx9v1m+UKow7yjvsrNSZpW5BHUwnSb8U5eK/5B7FAs49FctF7dQ6/FNaj2+ewU+fkAF/gxZqbcXHuxwWiK/X15au53LTxsdb2ep2+h+L1fdSvuPl7FI+361b5Q/ec46bOvWuNdUovHdrDv+g9iV9AnBlDJzBUY54YJ/0zMX9CuzRUPOA05JxAKGg5Bby4LFo9APcRBwhgmlOCR/Wkvb27kdO79yFjY1il4f0h/e32xve/+ztiZA77TztE9FGNEQ04BHVICmH9Lc2+8vd2rv300mlaqNB/DmoqS9p97xmL27wju04GW8SbtBe3WZpvnlP9QkVUur/U9oqn0j/XInI/2yayTcDwMqhImMKAqI8IP7Gam9x72/kXphYyX2WY3E8MOMdCLP1A87RgK1Wis13xDolpI2tjpTy/ojLV8NIGtNO/jHTKK6suJu66b59lPBy/xk853E3vZjr81y7Yt8Lcv6e9OHIGtj2scRY9jHgvgBjghp2hvIsxH3o8jnhHDKu93NHU3x/tamoHc0Bf3LmQLqXeRHHAsM1Y+2nWaEhYh4xEJOIzDRdbbYvzkwSmLN7cGXP83z+qtTnaGnJMS//q/34f0zNDIXCOjDe7fp7V8W7OmcParOd1QGuYwyf6MeErVdBIH0F0CFi4KI+CwQ1+ls0P22YT8fNv8V5uX/AVBLBwii0U0kuQgAAKcjAABQSwECFAAUAAgACACkbSRB1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAKRtJEGi0U0kuQgAAKcjAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAUAkAAAAA" " framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true" />


[math]\displaystyle{ x = \sin (180-t = \sin t }[/math]
[math]\displaystyle{ \cos (- t) = \cos t }[/math]

Dagens mentala kliv

  1. De trigonometriska funktionerna fungerar för vinklar som är större än 90o. De gäller inom hela enhetscirkeln.
  2. Cos t = x-koordinaten och sin t = y-koordinaten.
  3. Även det omvända gäller. Enhetscirkeln kan hjälpa oss förstå de inversa funktionen sin-1 och cos-1 som att man utgår får ett värde på axeln, går ut till cirkeln och mäter den motsvarande vinkeln.
Animationen visar grafen för funktionen y = sin x. Vinkeln är i radianer (där 2 pi motsvarar 360o

Trigonometriska ekvationer

Det trigonometriska ekvationerna har ofta flera lösningar.

Fördjupning: Här är en lösning till ekvationen sin v = o.5 i Wolfram Alpha. Den visar två lösningar till ekvationen (samt fler om man går ytterligare varv runt enhetscirkeln).

Övrigt

Konstigt facit: Bry er inte om bilden i facit till 1301.


Javascript och spel Kod: CC By SA spelprogrammering.nu

Intro Javascript_och_spel

Tänk! Öva matte på Mattecentrums_räknestugor

Öva på Khan: Unit circle

Läxa! Lös uppgifterna 1301-1309 och gärna fler.

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!


Lektion 5 - Triangelsatserna

Grader och radianer

360 grader motsvarar 2 pi radianer.

Öva på Khan: Omvandla mellan grader och radianer


Här finns material att hämta... http://en.wikipedia.org/wiki/Trigonometry

Areasatsen

Load video
YouTube
Areasatsen

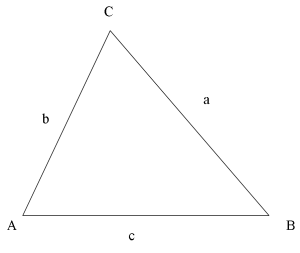[math]\displaystyle{ \mbox{Area} = \frac{1}{2}a b\sin C. }[/math]

Härledning

Triangeln borde ritas om så att sidan b är bas och horisontell.

Dra en höjd mot triangelns bas (sidan AC i detta fall).

  1. Höjden h = a sin C
  2. Triangelns area A = basen * höjden / 2
  3. Sätt in uttrycket för h ger:
Arean = 1/2 ab sin C


Wikipedia skriver om areasatsen

Läxa! Lös uppgifterna 1401-1405 och gärna fler.

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!


Lektion 6 Sinussatsen

Load video
YouTube
Sinussatse

[math]\displaystyle{ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} }[/math]

Härledning

  1. Ställ upp areasatsenför alla tre vinklar.
  2. Förläng med 2.
  3. Dividera med abc


Wikipedia skriver om sinussatsen

Läxa! Lös uppgifterna 1414-1421 och gärna fler.

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!


Lektion 7 Cosinussatsen

Lektion 8 Problemlösning

Uppvärmning

En reklambild från Facebook (till höger)

Vad bör man tänka på vid problemlösning?

  1. Rta Figur
  2. Sätt ut variabler och värden i figuren
  3. Välj Formel (eller sats)
  4. Utför beräkningarna
  5. Kontrollera om svaret är rimligt och om det finns flera svar



Ma3C: Problemlösning, sidan 34-35
Uppgift
Grupparbete

Denna lektion ska vi jobba med problemlösning i grupp. Ni väljer ett av problemen i boken och löser det tillsammans. Lösningen sk gå att presentera med projektor och ska lämnas in. Vem som helst i grupen ska kunna presentera den. Era lösningar kommer att publiceras på Wikiskola.

Ni får 20 minuter på er.

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!


Lektion 9 Cirkelns ekvation

Definition
Cirkeln
  • En cirkel består av de punkter som ligger på samma avstånd till cirkelns mittpunkt.
  • Avståndet från mittpunkten till cirkeln är radien.


Centrum i origo

En cirkel med radien 2.

En cirkel med centrum i origo och radien r kan skrivas på formen:

[math]\displaystyle{ x^2 + y^2 = r^2.\!\ }[/math]

En punkt på cirkeln har ett avstånd från origo som beskrivs genom Pythagoras. I figuren till höger är radien roten ur 4, dvs 2.

Wikipedia skriver om Pythagoras sats

Flytta cirkelns mittpunkt

En cirkel med radien 2

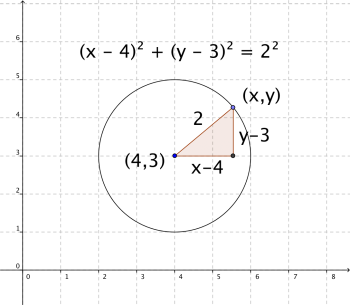
I ett koordinatsystem kan en cirkel med mittpunkt i (a, b) och radien r, beskrivas som mängden av punkter som uppfyller ekvationen

[math]\displaystyle{ \left(x - a \right)^2 + \left( y - b \right)^2=r^2. }[/math]


Ekvationen kan ställas upp genom utnyttjande av Pythagoras sats för avståndet mellan punkterna [math]\displaystyle{ (a,b) }[/math] och [math]\displaystyle{ (x,y) }[/math].

Se det som att man flyttar cirkelns mittpunkt från origo till punkten [math]\displaystyle{ (a,b) }[/math] genom att sätta in a och b i uttrycket ovan.

Exempel

Cirkelns ekvation är:

[math]\displaystyle{ 9=(x+2)^2+(y-3)^2 }[/math]

Den här cirkeln har sin mittpunkt i x = -2 och y = 3. Det är de värdena som ger noll inom respektive parentes.

Pröva att sätta in x = 0 respektive y = 0 ger punkterna där cirkeln skär axlarna.

Var skär cirkeln x-axeln?

Cirkel med glidare

<ggb_applet width="635" height="441" version="4.0" ggbBase64="UEsDBBQACAAIAGV2M0EAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAGV2M0EAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vjbjts2EH1OvmKgpxaIbVGUZCuwEzhBgwTYJAU2LdK+URItM9bFFSlfFvmdfkl/rENSkmVvdpsmQRE0yC4vM5zhXM5wtPOnhyKHHa+lqMqFQ8auA7xMqlSU2cJp1Go0c54+eTjPeJXxuGawquqCqYXja06R4iSOPELCeEQiPxr5EU1GkT8NR2QaJMxnKeOEOwAHKR6X1RtWcLllCb9O1rxgV1XClFG8Vmr7eDLZ7/fjTtW4qrNJlsXjg0wdwGuWcuG0k8co7uzQnhp2z3XJ5P3rKyt+JEqpWJmgfm1CI548fDDfizKt9rAXqVovnJAGDqy5yNZoUxAQByaaaYsO2fJEiR2XeHSwNDarYusYNlZq+gM7g7w3x4FU7ETK64XjjgPPm1E/9IMwjLyI+A5UteClank7nZNO2nwn+N6K1TPrZQdUVeUx0xLh40fwXM+FR3ogdvBwCENLcu2eS+3g2cG3Q2B5fHvct6y+5fEtj08d2Akp4pwvnBXLJXpQlKsao9evpTrm3Nyn3ThZTx6hTVLcIDN1MU2sy3HfdR/pnxB/fE2YnBtJBlpV3fxLpZ1KE9LPVel9laG0N5N6t3V6wR1mhvcotXZ/jp0kGLgWVZn/5ueWRnqfmZca7frrFIb+f2LifNJBZd6iA+Ra87bZo3ghNV5oBEGk055AgNgIp5jlAZAIh6kHiAYgAfgBLskMQj1OgU6R4AOFGWg+QsGAI5jhL39qhIUQoDC9O0VMAkFFPgQUiMGUD4gkMLhEjHoUOYIAAjyk1RNPi6Ah+CGu6Ax8vKOG5JQgI8WDuEb1HlACVB8mU/BCCLU84muohzN9dRTpQehCSLRARDUi2qIZ+WdAtTVh6y5Rbht15qKkSLupqrZ9LJAb69Gp6tn6dFYUH8xzFvMc34lrHUmAHcs1IoyiVVUq6IIY2r2sZtu1SOQ1VwpPSfjAduyKKX54gdyy0214k6qUP9eVel7lTVFKgKTK3f7OVU4Gc6+/NS7ogOAPCcGAEA7m00/qrZACjeSov6plx87S9JXmOJUG9OTbMj8+qznbbCtxbsZ8Yp6cOW+SXKSClb9ismot2i/wyRfIJ7S7SFWn10eJGQyH33ldYakidBwN/zlwtBRKonMKok8mTGPPv6BM8dAdpJnVzHd9gNiB97ZntUiH81fyWZWnvSeM8c/ZVjW16RywMtbapGWZ5dwkiIE1PsvJJq4O1zYzqJX17rjFlWv1x5lxOmBh8AJ0TdaOsR0Nj75Yz+UaHtdwuF2qibSnk8gzHGaM7Wi4MHft1VpDSWclcTs1Qppy5jpnoDGJrx/5phTqqlsokWxOlmr+N00R8z59zkWSbyZS3xnbDanet/2bnv82mL9bc8VsI0KDaDadBvjbi2Yzm6QX6Tnf8LrkeYsGTISmaqQF9wAoKU9EgUtLaB3KdLB/QQPsbsqzmnd256ans+42VHeY6Le2jagXdVW8KnfvMJMuLjCfdLecy6QWW52vEOMLsuGnnETbGT5A6fCchi+6LtEPDbpXadc+F/WGY1MJfLMzLxAUPIUMncJqjfpGrSvMo5d//blhJfyUY1snlchQARYvDJOGeM4L7OhAmUwum4LXIumjykyziBY0rZFk7FszdUihij9gVb3IhFN8kXxHrgPLt2sTWdJmNDvy+syPRtrrKu0Ut2pz3ZtCIfCxHSG2CnbA9xXlxRILrsLuHANXnrpze7O2YGFrozMLT3gzPTniFgn1bCUOvC8S6DNxgwnEzow5YU7hW7DBhleaJky1JcBMXoo05WV/W1Ziqpm4YDncWnMBXyJuYdQf3aL5pvgM0qQNzD+GKL4MkTd2/xch8voQ0XtDNMD29xqj+nuOkfsNUBQE3z+KDtsatWkxrYeXDuDmwvmBPYL4x06Q6QdsH3ke1JbQH/6S8Omvi8wOsR36CLqfGcHh6yN1FHRJ1kEweLmxr6f9U4C+sO5Xzhpcu3vxbA0dlVRFwcoUSvPJg09MknPn1IMz13iOEZ3W1sBGdYTECmtF3HIhvmEDVCRf5MK7EHC//96uVpIr7a4RNd4aBfST7r3VYQ3ylN6fp9gJ83KHdmDjDXBw20bm6NrrwU23c0DfjczWkbRbN2QQOMz2Whxg2fEvO66lpycRfhQtaSt0id8KI5MCS/xQGPWFhf9R2vtL24Xp7x+xEslltCfDvsJ0/u0fsZ78DVBLBwhJdoCiagYAAGETAABQSwECFAAUAAgACABldjNB1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAGV2M0FJdoCiagYAAGETAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAAQcAAAAA" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true"/>

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!


Det ligger ingen film att titta på till nästa gång.

Däremot vill jag att ni tittar på bilderna ovan en gång till. Sen vill jag att ni kikar på uppgiften som ligger på nästa lektion. ladda ner filerna och spar apå din dator och börja ändra i koden för att se vad som händer. Då kommer du att vara förberedd inför lektionen och få mycket mer ut av den.

Javascript - Cirkeln på parameterform

Det här är en digitalövning där vi ska titta på hur man ritar cirkeln på parameterform och hur det görs i javascript.

Det vi sett tidigare med cirkelns ekvation kallas att använda kartesiska koordinater. Problemet är att man inte kan lösa ut y som en funktion av x utan att ta roten ur. Roten ur ger ju som bekant två rötter, en positiv och en negativ. Det ställer till problem genom att en funktion bara ska ha ett y-värde per x-värde.

Man kan i och för sig tänka sig att rita de båda värdena samtidigt men det finns ett bättre sätt - polära koordinater

Parametrisering

Tänk på den rätvinkliga triangeln med hypotenusan r. Då kan man utgå från cirkelns mittpunkt i origo och beskriva x med cosinus och y med sinus som vi gjort tidigare. X- och y-koordnaterna uttrycks med hjälp av radien r och vinkeln t. Det kallas för parametrisering. r är parametern och t är en ny variabel, vinkeln. En parameter kan ändras från cirkel till cirkel vilket ger ändrad storlek (radie) men den ändras inte medans man ritar cirkeln. Gör man det får man helt andra former och det finns faktiskt exempel på det med på spelprogrammering.nu men det får du kolla på själv senare.

[math]\displaystyle{ x = r \cdot \cos t\, }[/math]
[math]\displaystyle{ y = r \cdot \sin t\, }[/math]

För r = 1 erhålls enhetscirkeln, det vill säga cirkeln med radie 1 och med mittpunkt i origo. t är i detta fall en vinkel som ökar från 0-360o.

Javascript

Javascript och spel Kod: CC By SA spelprogrammering.nu

titta först på funktionen cirkel. Sid 5 i boken spelprogramering.nu.

Sedan finns en del exempel hämtade från kapitel 8.


Idag ska vi äntligen jobba med Javascript!

Kartesiska koordinater

Uppgift
Prova att använda cirkelns ekvation och rita en cirkel.

Tips: du måste lösa ut y. (exemepelvis ur y2 + x2 = 400)

Ladda ner följande filer i en mapp och pröva själv genom att ändra i koden:

Facit: (klicka expandera till höger)


Polära koordinater

Titta på de här exemplen om hur enkelt man ritar cirklar med polära koordinater:

Mer: Testa funktionen att rita med polära koordinater i GGB.

Lektion 11 - Gör ett facit till trigonometriprovet

Uppgift
Formativ bedömning

jag tittar igenom och delar ut uppgifter till personer efter vad de behöver öva på.

Gemensamt arbete i Google Docs där provfrågorna redan ligger.

Skriv ditt facitsvar här: Trigonometriprov med facit

Genomgång och respons från mig på facit.

Förklara hur egenbedömning med generell matris går till.

Matrisen finns här: Generell bedömningsmaris Ma3C

Sedan egenbedömnig av proven

Facit ni gjorde inbäddat

Argument för självbedömning

Argument för självbedömning straxt efter mitten i filmen: http://www.ted.com/talks/daphne_koller_what_we_re_learning_from_online_education.html

Självbedömning

Nu har vi tittat på kunskapskraven, tillverkat ett facit och vi lärarare har satt betyg på era prov. Dessa betyg är dock hemliga en stund till. Nu ska du gå igenom ditt prov och bedöma uppgift för uppgift och fylla ett betyg som du tycker är rimligt på varje uppgift. Sedan väger du samman betygen tille tt betyg för varje typ av uppgift. På detta prov har det funnits uppgifter om:

  • Grundläggande trigonometri vilket är sinus, kosings, tanten, rätvinkliga trianglar och de trigonometriska funktionerna i enhetscirkeln. Detta heter sinus i mallen.
  • Cirkeln ekvation. Det heter cirkeln i mallen.
  • Trinagelsatserna. Det är areasatsen, sinussatsen och cosinussatsen.

Mallen för sjävbedöming som pdf finns även i wordformat

Hämtad från ”https://wikiskola.se/index.php?title=Trigonometri_Ma3C&oldid=32347”