Exponentialfunktioner

Jämför

Jämför med den allmänna formen för andragradsfunktionen:

[math]\displaystyle{ y = ax^2 + bx + c }[/math] (bortse från de sista termerna)

[math]\displaystyle{ y = ax^2 }[/math] (a är en konstant, vi kan lika gärna skriva c)

[math]\displaystyle{ y = C \cdot x^2 }[/math] (tänk nu att vi kastar om x och 2, C är en konstant )

[math]\displaystyle{ y = C \cdot 2^x }[/math] (här har vi ett exempel på en exponentialfunktion)

[math]\displaystyle{ y = C\cdot 1.5^x = C \cdot (\frac{3}{2})^x }[/math] (Vi kan ha olika tal som höjs upp i x)

[math]\displaystyle{ y = C \cdot 0.5^x = C \cdot (\frac{1}{2})^x = C \cdot (2^{-1})^{x}= C \cdot 2^{-x} }[/math]

på generell form:

[math]\displaystyle{ y = C \cdot a^x }[/math]

talet a kallas basen. x är exponenten

Växande

Tänk på pengar på banken med ränta varje år. Pengarna växer med ränta på ränta. 15 % innebär en tillväxtfaktor om 1.15 (förändringsfaktorn). Antag att man har 2000 kr från början. Tillväxten blir då exponentiell. Det tar bara fem år till en fördubbling.

Avtagande

Diagtrammet visar en avtagande funktion. Det startar på 100. Sedan minskar det med 10 per minut. Förändringsfaktorn är alltså 0.9

Vatten i termos

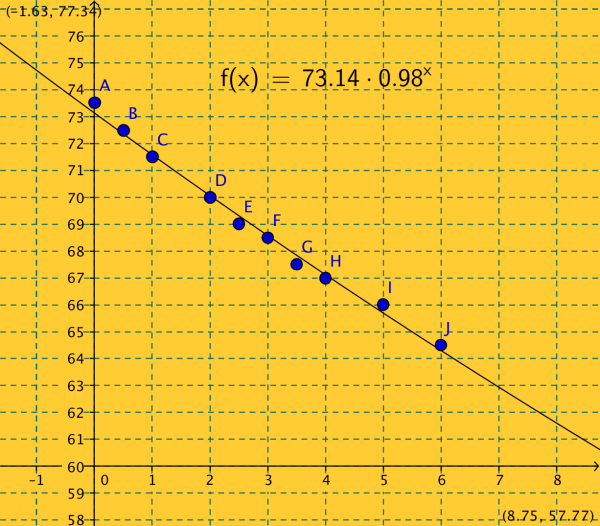
Figuren nedan visar temperaturen hos vatten som får svalna i en termos. Mätvärdena har lagts i en lista som heter avsvalning i GeoGebra. Därefter har kommandot RegressionExp[avsvalning] använts för att anpassa en exponentiell funktion till värdena i listan.

Du ser på funktionen f(x) att basen är 0.98 (= förändringsfaktorn)

Definitioner

y = Ca^x

växande a > 1

avtagande a < 1

C är skärningspunkt med y-axeln

a ej lika med 1, a > 0

Spegelkurvor

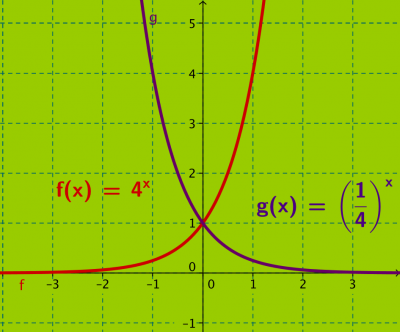
Spegelkurvorna nedan består av y = 4^x och y = (1/4)^x

4 och 1/4 är inverserna till varandra.

y = (1/4)^x kan skrivas som y = (4)^-x

Övning: Pröva att skriva in funktionerna nedan i GeoGebbra:

• y = (0.25)^x
• y = (1/4)^x
• y = (4)^-x

Vilken slutsats drar du?

Övning - GeoGebra

Rita själv funktionerna i bilden överst på sid 167

Skriv alltså in dessa funktioner ggb:

• y = 0.5^x
• y = 1^x
• y = 1.1^x
• y = 2*1.1^x
• y = 1.2^x
• y = 1.4^x
• y = 1.8^x
• y = 5^x

Fråga: Vad gör att en kurva ökar snabbare?

Exempel 1

Bestäm exponentialfunktionen där grafen går genom punkterna (0,2) och (5,6)

1. Sätt in x = 0 så får du C
2. Sätt in x = 5 och y = 6 i funktionen och räkna ut a

Uppgift
Lös upppgiften ovan med GeoGebra Skriv in funktionen y = C a <top>x<\top> Du kommer då att få frågan om du vill skapa glidare för C och a. Det vill du. Dsa i glidarna och finn lösningen.

Exempel 2

Lös ekvationen 2^x = 1 + 3x grafiskt.

Lös även olikheten 2^x < 1 + 3x