Integraler Ma4: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) |
||
| Rad 192: | Rad 192: | ||
{{uppgruta| '''Vad är <math> \lambda</math>?''' | {{uppgruta| '''Vad är <math> \lambda</math>?''' | ||
Läs på {{ | Läs på {{svwp| Exponentialfördelning}} och ta reda på hur <math> \lambda</math> förhåller sig till: | ||
# medelvärdet | # medelvärdet | ||
# standardavvikelsen | # standardavvikelsen | ||
}} | }} | ||
Versionen från 11 februari 2015 kl. 22.04
Förförståelsetest med NP-uppgifter
Följande uppgifter kommer från NP till den äldre kursen Matematik D. Tillstånd har inhämtats från Skolverket för dess publicering (under CC) på denna sida.
Ett kort test med uppgifter som testar förståelsen.
Fler uppgifter från nationella prov
Här är en samling uppgifter med integraler från gamla nationella prov:
Formelsamling på WikiBooks
Derivator och primitiva funktioner i en behändig formelsamling:
- Formelsamling på WikiBooks med derivering och integrering.
Integral och area
Hemuppgift
Gör bokens övning på sid 158.
Den handlar om arean under funktion
- [math]\displaystyle{ f(x) = \cos(kx) }[/math]
mellan skärningspunkterna med x-axeln.
k varierar från 1 till 5.
Länk till GeoGebraTube
Integralens värde och tillämpningar
Fritt fall
Titta gärna på wikipediatexten om fritt fall som ligger på förra avsnittet om diffekvationer.
Fysik och integraler - Hemuppgift
| Uppgift |
|---|
| Fysik och integraler
Lös någon eller några av uppgifterna hemma. Välj sedan en som du gör en snygg skriftlig redovisning av. Du ska vara beredd att gå fram och redovisa uppgiftens lösning på tavlan. Uppgifterna med sträcka hastighet är nog enklast. Du får sträckan genom att integrera hastighetsfunktionen. Problemlösning Fysik och Integraler Redovisning: På tavlan.
|
Numerisk lösning av integraler
Numerisk lösning av integraler
Läs vad Wikipedia skriver om Trapetsmetoden
Hemuppgift trapetsmetoden
Facit: (klicka expandera till höger)
Läs inte den här ledtråden förrän du har försökt själv med uppgiften. Lösningsförslaget i den länakde sidan är en GeoGebra som ska vara underlag för en diskussion på lektionen. Lösningsförslag till NP-uppgift fr vt 1999
Prova en svårlöslig integral med digitala verktyg
Kan du lösa denna integral analytiskt?
[math]\displaystyle{ \int {\sin(x^2)dx} }[/math]
Det är svårt att finna en primitiv funktion, eller hur?
Prova att lösa den med WolframAlpha och GeoGebra.
Läs mer här.
Formativ lektionskontroll
- Om allt gått väl kan alla nu lösa denna uppgift. I så fall kan vi gå vidare.
- Om det är många som inte kan detta måste vi repetera. Vi måste också diskutera, utvärdera och komma överens om hur vi ska göra för att lära oss detta.
- Om de flesta men inte alla kan detta kommer vi att gå vidare i klassen. De som ännu inte klarar detta får diskutera med mig hur de kan göra för att komma vidare.
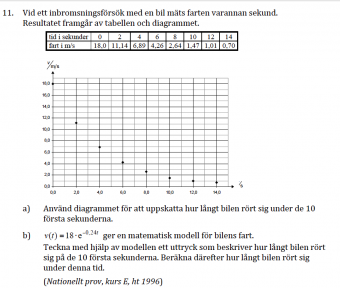
Lösningsförslag till NP E 1996 Integraluppgift
Sannolikheter med integraler
Definition


Normalfördelningen har täthetsfunktionen
- [math]\displaystyle{ f(x) = {1 \over \sigma\sqrt{2\pi} }\,e^{-{(x-\mu )^2 \over 2\sigma^2}} }[/math],
där μ och σ är normalfördelningens karakteristiska konstanter: μ är väntevärdet och σ är standardavvikelsen för fördelningen. Denna normalfördelning betecknas med [math]\displaystyle{ N(\mu,\sigma)\, }[/math].
Normalfördelningens täthetsfunktion kan inte integreras med vanliga endimensionella metoder eftersom den inte har någon primitiv funktion som kan uttryckas analytiskt. Arean under kurvan kan emellertid med andra metoder visas vara 1, vilket den måste vara för att vara en sannolikhetsfördelning.
En standardiserad normalfördelning har μ = 0 och σ = 1.
Filmer
Exempel 1 i boken
Hemuppgift - Normalfördelning

Lös uppgiften till höger.
Är det en normalfördelning och hur vet du det?
Använd datorn till att redovisa ditt svar.
Var beredd att presentera din lösning med projektor.
GeoGebra-förslag till lösning - NP Ma D Normalfödelning
Bedömningsanvisning från NP
Redovisad godtagbar förklaring, t ex integralens värde anger den totala ökningen av antalet bin under 24 veckor
Exponentialfördelningen

Exponentialfördelningen är kontinuerlig sannolikhetsfördelning med täthetsfunktionen
- [math]\displaystyle{ f(x;\lambda) = \begin{cases} \lambda e^{-\lambda x} & x \ge 0, \\ 0 & x \lt 0. \end{cases} }[/math]
Exempel på variabler som är approximativt exponentialfördelade är
- Tiden tills någon råkar ut för sin nästa bilolycka
- Tiden tills någon får sitt nästa telefonsamtal
- Avståndet mellan mutationer på en DNA-sträng
En viktig egenskap hos exponentialfördelningen är att den "saknar minne". Med andra ord, chansen att tillståndet kommer att förändras inom de nästa s sekunderna påverkas inte av den tid som redan förflutit.
Hemuppgift
| Uppgift |
|---|
| Vad är [math]\displaystyle{ \lambda }[/math]?
Läs på Wikipedia skriver om Exponentialfördelning och ta reda på hur [math]\displaystyle{ \lambda }[/math] förhåller sig till:
|



