Samband och förändring: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) |
||
| Rad 5: | Rad 5: | ||
{{:Procent Ma1}} | {{:Procent Ma1}} | ||
{{:Ränta}} | |||
{{ | |||
== 4.2 Funktionsbegreppet == | == 4.2 Funktionsbegreppet == | ||
Versionen från 5 november 2014 kl. 23.10
Kapitel 4 handlar om Samband och förändring och består av 14 delar.
4.1 Procent
Flipp: Introduktion till procent
Promille och ppm, 178-180
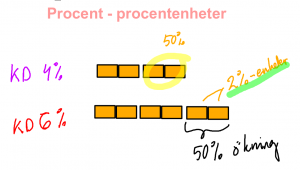
Procentenheter, 181-183
Ränta
Räkneexempel med uppgift 5 från Diagnos 6
Börja med att som repetition göra uppgift 5 från Diagnos 8. Gör det på det krångliga sättet (elevlösning) och jämför med hur enklet det blir med hjälp av förändringsfaktorn.
Kolla: Wolfram Alpha är enastående på uppgift 10.
Genomgång Ränta
Exempel 1 på sid 193 i boken Det lönar sig att lösa uppgiften i Excel.
4.2 Funktionsbegreppet
Vad är en funktion? 196-200
Följande GeoGebrafil har jag gjort själv. Den visar tre sätt att rita parabler.
genom att mata in ordet parabel samt ange tre punkter genom att angen linje och en punkt (styrlinje och brännpunkt genom att ange funktionen (inklusive start och stoppvärden = definitionsmängd)
Observera att de tre punkterna I, G, H på den blå parabeln motsvarar lösningen på Exempel 1 i boken sidan 197.
Filen finns på GeoGebraTube och heter Funktionsbegreppet med parabler.
Definitionsmängd och värdemängd, 201-203
GeoGebra-övning
Jag instruerar och eleverna prövar att rita en trinangel med omskriven cirkel.
4.3 Linjära funktioner
Linjära funktioner
Repetition: Förra gången stiftade vi bekantskap med en parabel som naturligtvis låter sig ritas i GeoGebra. En av kurvorna är precis den som kommer ur bokens Exempel 1 på sidan 197.
Man kan naturligtvis rita kurvan i Wolfram Alpha oxå. Det är bara att högerlicka på uttrycket i GeoGebra och kopiera till inmatningsfältet. Wolfram Alpha finns förresten som en Gadget till er som har Vistra eller 7:an.
- Lutning på GeoGebra.se
- taxifärd från Geogebrainstitutet
- linjär funktion med glidare från Geogebrainstitutet
Här kommer en grafisk lösning till exempel 2 på sidan 206 (GeoGebra):
Filen finns på GeoGebraTube.org och heter Ma2C exempel sid 206 linjära funktioner
Öka din förståelse av räta linjen med Geogebra
Filen är en översättning av en amerkiansk GGB. Min version finns på GeoGebraTube och heter Räta linjen k och m-värden.
Sidorna 204-208
info saknas
Räta linjen i Javascript
Bra interaktiv övning
Klurig läxa
4.4 Proportionalitet
Teori utifrån en diagnos
Titta på denna länk
- Uträkning till sista uppgiften på Diagnos 9 i Wolfram Alpha.
Sen har jag gjoret en busenkel GeoGebra om räta linjens ekvation (linjära funktioner). Den är gjord i tre steg. titta i konstruktionsprotokollet. Visa/ konstruktionsprotokoll.
Denna GGB finns på GeoGebraTube och heter Busenkel linjär funktion
Övningar
Här är en som är enkel:
http://geogebratube.org/student/m23347
Här är en bra men den ser inte snygg ut i Mac-Kan fixas till.
http://geogebratube.org/student/m23346
De bör bäddas in i sidan.
Direkt proportionalitet, 209-212
Teori
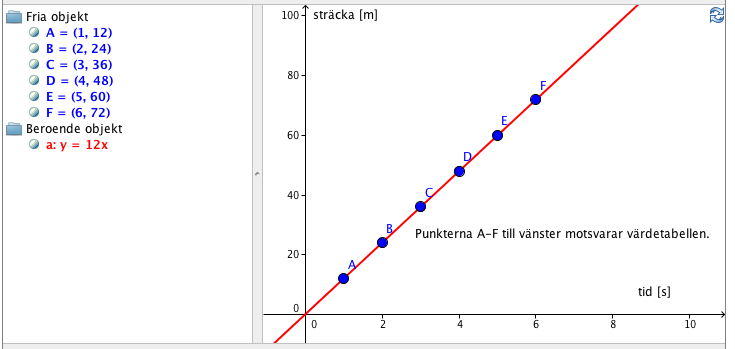
Direkt proportionalitet är å ena sida enklare än räta linjen. Det är ett specialfall när m = 0. Det betyder att linjen går genom origo.
Å andra sidan dyker proportionaliteten upp i en mängd sammanhang i exempelvis fysiken. Här kommer ett sträcka-tid-diagram (st-diagram). Det är teoriavsnittet i boken sid 209.
Exempel 1
Kommer snart
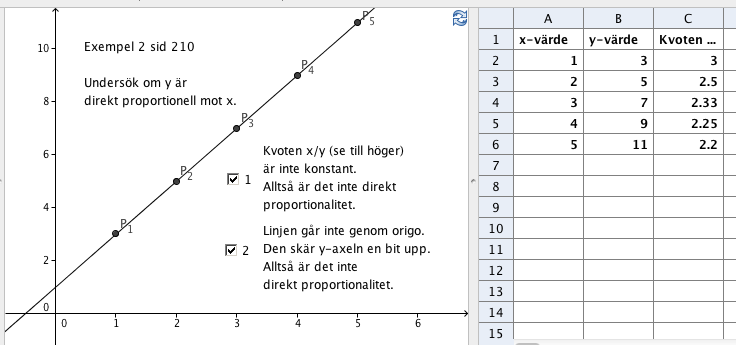
Exempel 2, sid 210
Den interaktiva GeoGebrafilen finns här: Ma1C Ex 2 s 210
Fler proportionaliteter, 213-215
måndag
Genomgång av Veckodiagnosen
Vi går igenom uppgift 3 och 5 från Diagnos 9. Trean kommer nedan men femman var enbart på tavlan.
Uppgift 3 löd så här:
3. Ulla lånar 180 000 för att köpa en bil. Lånet är med rak amortering på sex år och räntan är 5,6 %. Hur mycket måste Ulla betala varje månad?
Detta kan bli en mycket jobbig uppgift om man ska ge ett svar för varje månad. Det är ju 72 månader på sex år. Här får man själv göra några avgränsningar av uppgiften så att den blir rimlig.
Till att börja med kan man ju visa att man förstår att rak amortering innebär att beloppet delas upp i lika stora delar per månad.
180 000 / 6 = 30 000 kr per år 30 000 /12 = 2 500 per månad i amortering
Till detta kommer en ränta på det kvarvarande beloppet. Räntan kommer därför att sjunka månad för månad.
Här kan det räcka med att visa vad räntan blir för två eller tre månade, exempelvis efter en månad, 12 månader och 24 månader.
Excel
Om man vill kan man göra en kalkyl i Excel över lånekostnaden månad för månad.
Algebraisk lösning av uppgift 3
180 000 kr ==> Amortering 2500 per månad ränta 5.6 % ==> förändringsfaktorn 1.056
månad lån [tKr] räntekostnad att betala 1 180 180*1.056 2500+180*1.056 2 177.5 177.5*1.056 2500+177.5*1.056 3 175 175*1.056 2500+175*1.056 .. n 180-2500(n-1) 180-2500(n-1)*1.056 2500+(180-2500(n-1))*1.056
Månadskostnaden för månad nummer n är alltså 2500+(180-2500(n-1))*1.056
Intro - Fritt fall
Önskebrunnen på Tom Tits
Beräkning av djupet
s = at2/2
Vi hjälps åt med att ta tid. Genom att beräkna medelvärdet får vi bättre noggrannhet.
Mätning av djupet
En annan metod är att ta ett måttband och mäta djupet. Det visade att brunnen var ungefär 5 m djup.
4.5 Potensfunktioner
4.6 Exponentialfunktioner
Sidorna, 218-222
Här ett exempel från boken.
Filen finns på GeoGebraTube och heter Exempel fr Liber Ma1C, sid 216. Exponentialfunktioner.
4.7 Mer om grafiska lösningar
Sidorna 223-230
Teori
Filen ligger på GeoGebraTube och heter Liber Ma1C, exempel sid 223.
Vektorer
Vi skulle behöva repetera vektorer helt kort.
Öva matte
Repetition: Övning på räta linjens ekvation
Den här övningen är jättefin och har en egen sida.