Geometri 2C: Skillnad mellan sidversioner

Från Wikiskola
Hoppa till navigering Hoppa till sök
VisuellWikitext
Ingen redigeringssammanfattning
Rad 96: Rad 96:
== Vinklar ==
== Vinklar ==


Läs Ma2C s. 66-70
{{lm2c|Vinklar|66-70}}
{{#ev:youtube|mVIKaimXIlk|300|right}}


'''Genomgång'''
'''Genomgång'''
Rad 189: Rad 190:
* [http://www.matteboken.se/lektioner/skolar-7-9/plangeometri/kongruens-och-likformighet Matteboken]
* [http://www.matteboken.se/lektioner/skolar-7-9/plangeometri/kongruens-och-likformighet Matteboken]


=== TildaD - Kongruens ===
=== Topptriangelsatsen ===


Defination: Två figurer är kongruenta om de har samma form och samma storlek.
Den här filmen handlar om likformighet och topptriangelsatsen. Observera att sidan som är 15 lång i exemplet gäller sidan på hela den stora triangeln.
 
<youtube>TjX_BDyQG6o</youtube>
 
=== Kongruens ===
[[Fil:Kongruens_ja.png|thumb|300px|konguenta - samma form och lika stora]]
[[Fil:Kongruens_nej.png|thumb|300px|Icke-kongruenta - olika storlek]]
 
{{defruta|'''<big>Kongruens</big>'''
 
Två figurer är kongruenta om de har samma form och samma storlek.


Två trianglar är kongruenta om något av följande tre fall gäller:
Två trianglar är kongruenta om något av följande tre fall gäller:
# Två sidor och mellanliggande vinkel (SVS = Sida-Vinkel-Sida)
# Två sidor och mellanliggande vinkel (SVS {{=}} Sida-Vinkel-Sida)
# De tre sidorna (SSS = Sida-Sida-Sida)
# De tre sidorna (SSS {{=}} Sida-Sida-Sida)
# Två vinklar och mellanliggande sida (VSV = Vinkel-Sida-Vinkel)
# Två vinklar och mellanliggande sida (VSV {{=}} Vinkel-Sida-Vinkel)
}}


'''Länkar'''
==== Länkar ====


* [http://sv.wikipedia.org/wiki/Kongruens Kongruens-Wikipedia ]
* {{svwp|Kongruens}}
* [http://www.youtube.com/watch?v=TjX_BDyQG6o Kongruens-Youtube ]
* [http://www.matteboken.se/lektioner/skolar-7-9/plangeometri/kongruens-och-likformighet Kongruens-Matteboken ]
* [http://www.matteboken.se/lektioner/skolar-7-9/plangeometri/kongruens-och-likformighet Kongruens-Matteboken ]


Rad 207: Rad 218:
* [http://i39.tinypic.com/rvwv1s.jpg Bild 1 - kongruens ]
* [http://i39.tinypic.com/rvwv1s.jpg Bild 1 - kongruens ]
* [http://oi41.tinypic.com/dopiqx.jpg Bild 2 - icke kongruens]
* [http://oi41.tinypic.com/dopiqx.jpg Bild 2 - icke kongruens]
 
{{clear}}
<youtube>TjX_BDyQG6o</youtube>


== Extrauppgift på kul ==
== Extrauppgift på kul ==
Rad 249: Rad 259:


== Topptriangel- och transversalsatsen ==
== Topptriangel- och transversalsatsen ==
[[File:Topptriangelsatsen.png|thumb|Topptriangelsatsen]]
[[File:Transversalsatsen.png|thumb|Transversalsatsen]]
{{svwp|Topptriangelsatsen}}
{{svwp|Transversalsatsen}}


Tisdag v 8.
Det finns en PPT som förklararar dessa satser och ur de hänger ihop: http://wikiskola.se/index.php?title=Fil:Likformigheter_och_transversaler.pptx . Det är en kort ppt så dess bilder finns med här.
 
'''Håkans tips'''
 
* klippa in en bild från wiki'''media''' commons
 
Geogebra för att bevisa


=== NilsG Topptriangelsatsen ===  
=== NilsG Topptriangelsatsen ===  


81- 85
{{lm2c|Topptrinagelsatsen|81- 85}}


[[http://www.malinc.se/math/geometry/similartrianglessv.php MalinC Brättar om topptriangelsatsen]]
[http://www.malinc.se/math/geometry/similartrianglessv.php MalinC Brättar om topptriangelsatsen]
<youtube>tus1huYtw8w</youtube>
<youtube>tus1huYtw8w</youtube>


Rad 269: Rad 277:
<ggb_applet width="796" height="336"  version="4.0" ggbBase64="UEsDBBQACAgIAPu7VUAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAD7u1VAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1a2ZLbNhZ9dr4CpYd5mUjCDsKjdspbKq5ylqr2TE3NyxQlQhLTFKmQVC+p/E6+ZH5sDgBSq+3u9pK002U1SOIS9+Kcu0HtyTfXq4JcurrJq/JswEZ0QFw5q7K8XJwNNu18mAy+efLVZOGqhZvWKZlX9SptzwbSS+bZ2cCYuRaap0Mt0/lQ8mw+tEa54XzK05nTZiaT+YCQ6yZ/XFY/pCvXrPH8fLZ0q/R1NUvboHjZtuvH4/HV1dWoVzWq6sV4sZiOrptsQGBm2ZwNuovHWO7gpSsRxDmlbPzv71/H5Yd52bRpOXMD4rewyZ989WhylZdZdUWu8qxdng0SKgdk6fLF0u/JsAEZe6E1AFm7WZtfugav7t2GPber9SCIpaWffxSvSLHdzoBk+WWeufpsQEfCWq6EEUxIwROhzIBUde7KthPulY775SaXubuK6/qroBJmtlVVTFO/JPntN8Ipp+RrP7A4cAxaxykan1ERBx4HGQcVZWR8XUZRGWVklJFiQC7zJp8W7mwwT4sGEOblvAZ92/umvSlcsKd7sNs++xp7avJfIcwo/CRiHm6+9h+Nj/QT48NNsj2tbb25p9JepTT3UMk/RqXoVQrOTlVy9Y5d6veAG224yzaZ2tsmVIV/4XOiUfB7aIz3tykUiVdoEvlWhVr+IVucjPtImXTBQZqll+2YbN2q8eEiLFHWez0jCqGhDZxcEWYxGE4QDIQpIhVuWUK0Hw0RBhOSCJIQL8cECbGhEvySJiymicJi/qlBSBIGRZIoQVgIKUkQSCSEJUKUC0goRRRe8uoZ90sITaTGnUiIhI0+Ig2DoMCLuId6TgQjwr/MDOGaaL8ekz7SdeJNx5KcaEo08wsiqBHQMZghnxDhd6M7uPJyvWkPIJqtsv6yrdZbLiCNdLTLejE9HSTFR5MinboCdeLcM0nIZVr4iAiK5lXZkp5EHp8t6nS9zGfNuWtbvNWQn9PL9HXauutvId30uoPsrCqbn+qqfV4Vm1XZEDKrCrq1uSrY3jXfWo0bsTch9yfU3oTeuzZv1VthhmwaB/1V3fTiaZa98hK71AAkfyyLm2e1Sy/WVX64jck4lJyJ28yKPMvT8l9wVq/F40L6ChSyVV+BBEt6Q6o6O79p4MHk+j+urjBHR1xQavAjFVWJRR25iVM80SONUiYox+/EUJ+YZqkPPm5HzEjGE8OUMlxohbf6uZFNLE14YoVMEsl11O0utxSl126320XtQ3vv5lXzrCp2jwIAz9N1u6lD9wAjar+tp+WicMFJQmijNM8uptX1efQOEdd6c7PGHY0WTBcBeILkwH2BXnTjFKNSUcabtpWiQYYGCdq7W55t55nlQSKM0zgGKfhvNK3bKuu3yWivJm9CSqODLnD6dOW931f6TZm3r/ubNp9d7LbqX/hhs5q6rQ8drsk+1ZqT8ZGTTS5cXbqi82mQuak2TQzRPXfP3Cxf4TZOdJCknq5/woD4NHOL2vWGF6Ezi4CFWbrvriePw1Lf1tXqVXn5Br5wZMBk3Fs5aWZ1vvY+R6aoAxdu51VZ3qQoI9n+ez4IsfWZLxeAp/XQIDw37bIC2d/97/eLtCQvC/RfTZsvsAayDCR8LBZuhc6LtMHdgsduYX8aejqPL6mmPyPRbWthnN8RiOm3up53TpIW62Xq+74OhCK9cfUBLGG976vsGCxwEXaEqF/7BTzba+eio0SLcbHGgiG+DvIW8G/Ite/LJaOIaqUNek7p/f0GtXNEubUW7R0VqJ7IMuTX2O3Hdtfj4OPxIInHp0ekwtMihLeA+exhgfkhUDJo5UmSsIRzrQW3MmDJ1EgIyRSaecV9U//ZsXz+5WNpRowrzaWyOkErzk2A0tiREYoZPFJGWP1JkJxVq1VaZqQMzeZPVXGzqMrBrv1JqQ91kjLvpCTlHt8I3qbt57u3WBSbRbEUA/qLaVTYqXkLdVFhT852qcNy06IVusBxrwlHkLarfuHiuzzLXGiDx+/nfQ/pfeKZEoF6xbp6uGOe3Yf5d7tn4xb+bmvI7BYHvb+h93TRnaMNEbUCh1ot0NEgdgUXXQbUzFgLL1T4JJRHX4NfWk6ttgZNEDVMHrcFd+fJ/VLGV5pYq/PVushnebt1rsLHx6uyRVVyoXSdFuQL59a+E/qxfFOnZeO/bIkye4X+jpykD4gTjapEGeUS7alCwxmjf4j+kyKJGu4JEcixJpCiLShMLPIFY8Jaw/4ynEwfDidGjgxVDBGiFcBWtqcEMWCERLsgQIvwdQOUDAWqXqJ9NGlqkcZP2ucHzMlxQfCl9bAcTE8KwIvbkvx+fX7xQfUZaSieSfz4MJpHNZIWZ0VBhTbwAqODUwg5SpBNheKGWTRCn6FKv4YfHXHyoq+9x9Rk76fGu+QW+ezDAu7wOPmHV6Uh0t6IMVQmg9woeMLF5wm3dxOyDb8jVrLISnrCysv7BMzLDwoYHb8J0PGLAD98PDFC+kQIj/d+ryzgjj2+pobD6yXiAC2+pdHphWUQRvtqZSJ0wrX6hDFw3hWLQ8CfR8BfnAA+fz/gx6Vn/tFniE8SCBK5xGohBX6METEKhmykUWAoU5oyBlRZV3VYYkdAWXL/tRf6BjQIX2rZeTu7XZJ7esKuux+77mGwy0EXRYZDdDDNNE9kzy9NkPK41L7ZThLZ0cv1iAqJ6FKCQ1x9pjT3p9H7LNL78oTexf3oXTwMeocc9Qo5MvEHeJQsybf8MpVIpa3UXCQ+pwaCuUFDgYOV5Examyj5Vwvfl5Hf0+8Plvfjd/lA+BUJDgXCSIlQ5GovfPEokG6VlpbZWA0lkyPLqK+PGsc7pvUXRK+7XtcwzHfMHcgXl1X7X7TImMGyZEy6v4MdUlduVq7OZ4Ojt7x+6Np00LKRopqh39PWotbpxNydPnZHU3ln6hKmLu5sKr/V1E9q6Rt33faY/u2XTdX+Yz52Z/GK/J30mJ8a3+LFweEqf2Yr37Rp3YajIwlt40gwg4TnQ0LiPGxViBSdID8qSgXFIdoqcXBUuh0ofgDUcrw4AorfCSj+kIDCuYehczNGaZR4RXk8UmoDoOBzOPpIiVNl8i6gxvt/6gl/Uu3+d9CT/wNQSwcI4u9Zvw0JAAC6JAAAUEsBAhQAFAAICAgA+7tVQEXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICAD7u1VA4u9Zvw0JAAC6JAAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAKUJAAAAAA==" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
<ggb_applet width="796" height="336"  version="4.0" ggbBase64="UEsDBBQACAgIAPu7VUAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAD7u1VAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1a2ZLbNhZ9dr4CpYd5mUjCDsKjdspbKq5ylqr2TE3NyxQlQhLTFKmQVC+p/E6+ZH5sDgBSq+3u9pK002U1SOIS9+Kcu0HtyTfXq4JcurrJq/JswEZ0QFw5q7K8XJwNNu18mAy+efLVZOGqhZvWKZlX9SptzwbSS+bZ2cCYuRaap0Mt0/lQ8mw+tEa54XzK05nTZiaT+YCQ6yZ/XFY/pCvXrPH8fLZ0q/R1NUvboHjZtuvH4/HV1dWoVzWq6sV4sZiOrptsQGBm2ZwNuovHWO7gpSsRxDmlbPzv71/H5Yd52bRpOXMD4rewyZ989WhylZdZdUWu8qxdng0SKgdk6fLF0u/JsAEZe6E1AFm7WZtfugav7t2GPber9SCIpaWffxSvSLHdzoBk+WWeufpsQEfCWq6EEUxIwROhzIBUde7KthPulY775SaXubuK6/qroBJmtlVVTFO/JPntN8Ipp+RrP7A4cAxaxykan1ERBx4HGQcVZWR8XUZRGWVklJFiQC7zJp8W7mwwT4sGEOblvAZ92/umvSlcsKd7sNs++xp7avJfIcwo/CRiHm6+9h+Nj/QT48NNsj2tbb25p9JepTT3UMk/RqXoVQrOTlVy9Y5d6veAG224yzaZ2tsmVIV/4XOiUfB7aIz3tykUiVdoEvlWhVr+IVucjPtImXTBQZqll+2YbN2q8eEiLFHWez0jCqGhDZxcEWYxGE4QDIQpIhVuWUK0Hw0RBhOSCJIQL8cECbGhEvySJiymicJi/qlBSBIGRZIoQVgIKUkQSCSEJUKUC0goRRRe8uoZ90sITaTGnUiIhI0+Ig2DoMCLuId6TgQjwr/MDOGaaL8ekz7SdeJNx5KcaEo08wsiqBHQMZghnxDhd6M7uPJyvWkPIJqtsv6yrdZbLiCNdLTLejE9HSTFR5MinboCdeLcM0nIZVr4iAiK5lXZkp5EHp8t6nS9zGfNuWtbvNWQn9PL9HXauutvId30uoPsrCqbn+qqfV4Vm1XZEDKrCrq1uSrY3jXfWo0bsTch9yfU3oTeuzZv1VthhmwaB/1V3fTiaZa98hK71AAkfyyLm2e1Sy/WVX64jck4lJyJ28yKPMvT8l9wVq/F40L6ChSyVV+BBEt6Q6o6O79p4MHk+j+urjBHR1xQavAjFVWJRR25iVM80SONUiYox+/EUJ+YZqkPPm5HzEjGE8OUMlxohbf6uZFNLE14YoVMEsl11O0utxSl126320XtQ3vv5lXzrCp2jwIAz9N1u6lD9wAjar+tp+WicMFJQmijNM8uptX1efQOEdd6c7PGHY0WTBcBeILkwH2BXnTjFKNSUcabtpWiQYYGCdq7W55t55nlQSKM0zgGKfhvNK3bKuu3yWivJm9CSqODLnD6dOW931f6TZm3r/ubNp9d7LbqX/hhs5q6rQ8drsk+1ZqT8ZGTTS5cXbqi82mQuak2TQzRPXfP3Cxf4TZOdJCknq5/woD4NHOL2vWGF6Ezi4CFWbrvriePw1Lf1tXqVXn5Br5wZMBk3Fs5aWZ1vvY+R6aoAxdu51VZ3qQoI9n+ez4IsfWZLxeAp/XQIDw37bIC2d/97/eLtCQvC/RfTZsvsAayDCR8LBZuhc6LtMHdgsduYX8aejqPL6mmPyPRbWthnN8RiOm3up53TpIW62Xq+74OhCK9cfUBLGG976vsGCxwEXaEqF/7BTzba+eio0SLcbHGgiG+DvIW8G/Ite/LJaOIaqUNek7p/f0GtXNEubUW7R0VqJ7IMuTX2O3Hdtfj4OPxIInHp0ekwtMihLeA+exhgfkhUDJo5UmSsIRzrQW3MmDJ1EgIyRSaecV9U//ZsXz+5WNpRowrzaWyOkErzk2A0tiREYoZPFJGWP1JkJxVq1VaZqQMzeZPVXGzqMrBrv1JqQ91kjLvpCTlHt8I3qbt57u3WBSbRbEUA/qLaVTYqXkLdVFhT852qcNy06IVusBxrwlHkLarfuHiuzzLXGiDx+/nfQ/pfeKZEoF6xbp6uGOe3Yf5d7tn4xb+bmvI7BYHvb+h93TRnaMNEbUCh1ot0NEgdgUXXQbUzFgLL1T4JJRHX4NfWk6ttgZNEDVMHrcFd+fJ/VLGV5pYq/PVushnebt1rsLHx6uyRVVyoXSdFuQL59a+E/qxfFOnZeO/bIkye4X+jpykD4gTjapEGeUS7alCwxmjf4j+kyKJGu4JEcixJpCiLShMLPIFY8Jaw/4ynEwfDidGjgxVDBGiFcBWtqcEMWCERLsgQIvwdQOUDAWqXqJ9NGlqkcZP2ucHzMlxQfCl9bAcTE8KwIvbkvx+fX7xQfUZaSieSfz4MJpHNZIWZ0VBhTbwAqODUwg5SpBNheKGWTRCn6FKv4YfHXHyoq+9x9Rk76fGu+QW+ezDAu7wOPmHV6Uh0t6IMVQmg9woeMLF5wm3dxOyDb8jVrLISnrCysv7BMzLDwoYHb8J0PGLAD98PDFC+kQIj/d+ryzgjj2+pobD6yXiAC2+pdHphWUQRvtqZSJ0wrX6hDFw3hWLQ8CfR8BfnAA+fz/gx6Vn/tFniE8SCBK5xGohBX6METEKhmykUWAoU5oyBlRZV3VYYkdAWXL/tRf6BjQIX2rZeTu7XZJ7esKuux+77mGwy0EXRYZDdDDNNE9kzy9NkPK41L7ZThLZ0cv1iAqJ6FKCQ1x9pjT3p9H7LNL78oTexf3oXTwMeocc9Qo5MvEHeJQsybf8MpVIpa3UXCQ+pwaCuUFDgYOV5Examyj5Vwvfl5Hf0+8Plvfjd/lA+BUJDgXCSIlQ5GovfPEokG6VlpbZWA0lkyPLqK+PGsc7pvUXRK+7XtcwzHfMHcgXl1X7X7TImMGyZEy6v4MdUlduVq7OZ4Ojt7x+6Np00LKRopqh39PWotbpxNydPnZHU3ln6hKmLu5sKr/V1E9q6Rt33faY/u2XTdX+Yz52Z/GK/J30mJ8a3+LFweEqf2Yr37Rp3YajIwlt40gwg4TnQ0LiPGxViBSdID8qSgXFIdoqcXBUuh0ofgDUcrw4AorfCSj+kIDCuYehczNGaZR4RXk8UmoDoOBzOPpIiVNl8i6gxvt/6gl/Uu3+d9CT/wNQSwcI4u9Zvw0JAAC6JAAAUEsBAhQAFAAICAgA+7tVQEXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICAD7u1VA4u9Zvw0JAAC6JAAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAKUJAAAAAA==" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
<br>
<br>
=== Euklidiskt bevis av Transversalsatsen ===
{{uppgruta|Bevisa Transversalsatsen
Gå till sidan [http://www.malinc.se/math/geometry/transversalsv.php MalinC om Transversalsatsen] och följ hennes instruktion om hur du bevisar transversalsatsen.
här får du göra det "Euklidiska" beviset som bygger på jämförande av areor. Detta är en uppgift på C-A-nivå
}}


== Randvinklar och medelpunktsvinklar ==
== Randvinklar och medelpunktsvinklar ==
Rad 316: Rad 332:
<br />
<br />


=== FredrikJ-Bisektrissatsen ===
=== Bisektrissatsen ===
{{#ev:youtube|2qu4iExU0rA|340|right|Bisektrissatsen}}
 


'''Länkar'''
'''Länkar'''
* [http://www.youtube.com/watch?v=2qu4iExU0rA videoklipp på bisektrissatsen ]
 


* [http://matteformler.se/images/geometri16.png bild på bisektrissatsen  ]
* [http://matteformler.se/images/geometri16.png bild på bisektrissatsen  ]
Rad 328: Rad 346:


  Bisektrissatsen = AD / BD = AC / BC
  Bisektrissatsen = AD / BD = AC / BC
{{clear}}


=== AntonL - Kordasatsen ===
=== AntonL - Kordasatsen ===
Rad 335: Rad 354:
<youtube>-0vOVQlhQbQ</youtube>
<youtube>-0vOVQlhQbQ</youtube>


== Koordinatgeometri ==
== Repetition och sammanfattning av geometrin ==
s. 92- 101
 
Torsdag v 8.
 
=== RikardM - Avståndsformeln ===
<youtube>FY6G0-ByfrA</youtube>
 
=== WilliamM - Mittpunktsformeln ===
 
 
[[Bild:Mittpunktsformeln.png|thumb|200px|"P1" är punkten 1, "P2" är punkten 2, och "M" visar var exakt var mitten av punkterna P1 och P2 är. Bilden är tagen från Wikipedia.]]
 
'''[http://sv.wikipedia.org/wiki/Mittpunktsformeln Mittpunktsformeln]''' är en mattematisk ekvation.
Två punkter P1 och P2 som kan ligga precis var som helst i
ett  kordinatsystem, med hjälp av mittpunktsformeln bestämma
punkten mitt emellan Punkt1 och Punkt2 som har benämningen M.
 
 
'''Definition 1:'''
 
(X1,Y1) och (X2,Y2)
(Xm,Ym)= (X1+X2/2),(Y1+Y2/2)
[http://www.youtube.com/watch?v=EhRbyxoD6Io Förklaras i videon]
'''Definition 2:'''
Det gick inte att placera definitionen från Wikipedia, eftersom den inte stöds,
gå in på länken och se efter själv:[http://sv.wikipedia.org/wiki/Mittpunktsformeln Wikipedia, Mittpunktsformeln]
O = Origo.
M = Punkten mellan P1 och P2.
P1 = Punkt1.
P2 = Punkt2.
 
'''Exepel på problem'''
Du har två punkter (1, -2) och (-3, 5), hitta mittpunkten av de två punkterna med hjälp
av [http://sv.wikipedia.org/wiki/Mittpunktsformeln mittpunktsformeln].
 
'''Lösning'''
y 1 = -2, x 2 = -3 och y 2 = 5.
 
 
 
 
'''LÄNKAR'''
[http://translate.google.se/translate?hl=sv&langpair=en%7Csv&u=http://cs.selu.edu/~rbyrd/math/midpoint/ Exempeluppgift]
[http://ungdomar.se/forum.php?thread_id=223534&page=1 Svårare Exempeluppgift]
[http://www.youtube.com/watch?v=EhRbyxoD6Io [[Film om Mittpunktsformeln]]]
[http://www.khanacademy.org/exercise/midpoint_formula [[Khan Acadamy]]]
 
=== FelixN - y=kx+m ===
        K = lutningen. Man kan räkna ut K om man har två koordinater t ex x1-x2/y1-y2 = K
        M = Var linjen skär y-axeln
        Exempel uträkning med koordinater.
        (-1,1) (1,5)
        y= valfri Y-koordinat, vi väljer 5. Formeln blir då 5=kx+m
        vi räknar ut k
        k=(x1-x2)/(y1-y2)= 5-1/1-(-1) = 4/2 = 2, k=2. Formeln blir då 5 = 2x+m
        x = 1. Formeln blir: 5 = 2*1+m. Tar bort 2 på båda sidor.
        M= 3
[[Fil:http://upload.wikimedia.org/wikipedia/commons/0/0e/FuncionLineal04.svg]]
Länkar:
 
http://www.youtube.com/watch?v=obtLcSrvE_Y
http://sv.wikipedia.org/wiki/Linj%C3%A4r_ekvation
 
== Riktningskoefficienten ==
s. 102 - 104
 
'''Håkan länkar'''
* [http://www.theducation.se/natstod/ma-nv/exempel/trana_pa_ekvation_till_rat_linje/ Theeducation]
* [http://www.khanacademy.org/exercise/graphing_linear_equations Khan: Graphing linear Equations]
* [http://www.khanacademy.org/exercise/line_graph_intuition Intuitiv Khan]
 
=== SamN - riktningskoefficienten ===
 
[[File:Slope picture.svg|thumb|Slope picture]]
 
Bestäm riktningskoefficienten för den linje som går genom punkterna (1.2) och (4.-3)
 
'''Uträkning för riktningskoefficienten'''
 
-3-2/4-1= -5/3=-5/3
 
http://www.matteguiden.se/wp-content/uploads/2010/01/linjes-lutning-4.png
 
http://www.matteguiden.se/wp-content/uploads/2010/01/linjes-lutning-3.png
 
 
''' Definition '''
y = kx+m
 
{{clear}}
 
'''Ett Exempel + uträkning till exemplet'''
 
'''Fråga 1'''
 
Erika anställer en städslav och får betala för ''4 timmar 450 kr'' och för ''9 timmar 990 kr''
Erika betalar både grundavgift och en avgift per timme. Hur stor är avgiften Erika måste betala?
 
'''Uträkning till fråga 1'''
 
Tänk så här:
 
Kostnaden ökar med
990kr-450kr= 540kr
 
Tiden ökar med 9-4= 5timmar
990-450/9-5=540/2= 225
 
Avgiften per timme blir = 225 kr
 
'''Länk'''
 
[[http://www.youtube.com/watch?v=vzkUI5W2sZQ riktningskoefficienten ]]
 
== lov ==
 
== Räta linjens ekvation ==
 
Onsdag morgon
 
s. 105-109
 
För att rita en rät linje eller för att skriva dess ekvation behöver du antingen:
 
# två punkter på linjen ''eller''
# en punkt på linjen och dess lutning
 
En punkt på linjen kan vara att veta var den skär en axel, exempelvis y-axeln.
 
== Parallella och vinkelräta linjer ==
 
Onsdag 10.30-12
 
s. 110- 112
 
Två linjer är parallella om de har samma riktningskoefficient.
 
'''Parallella linjer'''
k<sub>1</sub> = k<sub>2</sub>
 
Två linjer är vinkelräta om produkten av riktningskoefficienterna är minus ett.
 
'''Vinkelräta linjer'''
k<sub>1</sub> * k<sub>2</sub> = -1
 
<br>
<ggb_applet width="498" height="595"  version="4.0" ggbBase64="UEsDBBQACAgIANy8ZUAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICADcvGVAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbNVYW2/cNhZ+Tn8FoYd92M1oeBeVHadogi0awL0ATouiLwtK4ozV0UiqRI1niv6d/pL9Y3tISnOz48Tb2yawTZE8PIfnO1dm8eluU6Gt6fqyqa8iEuMImTpvirJeXUWDXc5U9OnLTxYr06xM1mm0bLqNtlcRd5RlcRUly6USQi9nGZXpjBcpn2WFpDOaZKmiJktxkkcI7fryRd18pTemb3VubvJbs9HXTa6tF3xrbftiPr+7u4snUXHTrearVRbv+iJCcM26v4rGjxfA7uzQHfPkFGMy//7L68B+Vta91XVuIuRUGMqXnzxb3JV10dyhu7Kwt1eRwDJCt6Zc3YJOCVMRmjuiFgBpTW7Lrenh6MnU62w3beTJdO32n4UvVB3UiVBRbsvCdFcRjkmaSKq4UDxVmLIkQk1XmtqOtGSUOZ+4LbaluQts3ZeXyCNkm6bKtOOIfvkFUUwxeu4GEgYKg5RhC4c1zMJAw8DDIAIND8d5IOWBhgcaziK0Lfsyq8xVtNRVDwiW9bID6x3mvd1Xxt9nXDhqT56DTn35MxATDG4SIPeT5+5Xwi93G/NzJcmJVNsNTxQ6iQSUP1wk/U2KskfVpOIdaspHhAa9P0RPIk5kgij/43/vSWSPqXkpMczfJ5ApJzBR/EGBkv8pKi7mU6gsxuhA/a2jHb3Hmk3v4oWlSKTO7QkSEBsyAS8XiKQwJBRBNCAiEBcwJQpJNyaIJbDBEUMKOTrCkA8OoeAPTzwziQQwc6sJxCQiIIgjwRDxMcURRBLycQkxShlQCIEEHHLiCXUsmERcwowpxOGOLiQTAoQMDsIcxFPECGLuMEkQlUg6foS7UJfKXR1YUiQxksQxhKiGiA7RDPQKMaeNHOEq63awZxDlm2L6tE17sAVQQz46Zr2Qn86S4rNFpTNTQZ24cZZEaKsrFxFe0LKpLZqMKMPaqtPtbZn3N8ZaONWjH/VWX2trdp8DdT/J9rR5U/ffdI193VTDpu4RypsKH+7cVOTkmx5uDRN2ssFPN8TJhjz5Th6U28AOGnoD8puun8h1UbxxFMfUAEh+XVf7V53R67Ypz9VYzH3JWZghr8qi1PV34KxOisMFTRXIp6upAgmZTBdpuuJm34MHo90PpmugOiUxSyXljAlBGJUQJfuwIwiNlUyZSIVQInUlrc+1Cz2uYqawTKRIhEqSFGrP/h1bhAfJZnswkN6Zg+6rrixOv9/0r5qqOCDhlX+tWzt0vnOAzNg5lT6rV5XxDuLDGspyvs6a3U3wDBZ4vd23MMNBfrbyoCNIDFCIgGAcMxiFCDTuYgcq7Gmwp8CTq5XFYZ+k1FP4MQujpwLfDVcbFSWTlgRPYsrepzMcnQWNd3xX5Ie6tNfTxJb5+qipo/9q2GTm4D7nLMnvxHIxv3Cvxdp0talGbwZDDs3Qh+A8cfTC5OUGpmFjBEQ7Y30LFwirhVl1Zrp35XuyAJffxaeOem/Zs/q8azZv6u1b8ISLCyzm0y0Xfd6VrfM3lEEFWJujTxVlr6GAFKfnXPiB6rkrFACPddBAYA72tgFTf/GfX9e6Rv+qoPPqbbkCHpBfgMJFYWU20HQh653N++sB9s98N+fwRU32I6S4C7Mc7QfbDzqec02kq/ZWu45vBKHSe9OdweL5fdkUl2CBLbxGEO9tsHVrTPCScF/4aIGdj62zfAXo92jnOndIDZADKFZU4TRRkAT2cK8YQ9sJ3YgUNIXeD1Z/Dm1+6HMdDC4Yz7J3WL2wKThaQPA9WL76+LGUMeZJymWSYObSaSo8liLGkjAMCVsIKVPMfhcs82az0XWBat8bXUNOio6lWmPnnEgTh2sAbbDThg6sRgb3zOLS2wF1/R6rnODwLrPg/90oR2hnNIbXEEt5Ck+WRCoA2WPLY04ZFUxIihPwX+KxnXGoUZKJhEoMxnCV7SJzW+go1vBs6n0rb8dC4j++KIvC+G4y1LWf6nCkDwnV7NqqzEv7FN9+/fH7No0lkYpyxRVLxi7CebxMOVGK4VQpwbn6A1z76w6S9KqpdfWAk78OTq7vOXn2BCfP/l+c/AFv3r/D9wFmRmKeppxCD0YVJUSxP97Lz01zUzXtpUXum2L9uCnqYWO6Mj+gvfYMAaFhwimWCVVpQqCLDU4YRPyWeDq1F/lAe91r/z4U3qcBmN0H8N/kiRDCgQsQZ+AsSpLjP5x8xCiCe3ZwwqW08bLw+ioiBOugPfo7cgj41+jjQPlT95HCT1T78au9NTtLxrv97aehsf90Yoe1BdXCHP0DuSUYwjz8fUgBePUey0pg/FfmLv9e7wHS5fFtOz3ep1QykvZWd/Ybl/qRy3UsxgmBB6kSGDpPSplPdSpW3L0uoXhDWYHyfVpPTlGenzb0/sk8/u/vy/8CUEsHCJp/FVf7BgAAmhYAAFBLAQIUABQACAgIANy8ZUBFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgA3LxlQJp/FVf7BgAAmhYAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACTBwAAAAA=" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
<br>
<br>
=== SimonS - parallella och vinkelräta linjer ===
[[File:Parallel Lines.svg|thumb|Parallel Lines]]
 
http://www.youtube.com/watch?v=nZuko8vyVs4
<youtube>nZuko8vyVs4</youtube>
 
http://www.matteboken.se/lektioner/matte-2/funktioner/linjara-funktioner-y-=-kx-plus-m
 
Ytterligare en sida för dej som fortfarande inte förstår vad det handlar om.
 
http://www.malinc.se/math/functions/perpendicularlinessv.php
 
Fin sida för dej som satsar på högre betyg på provet än E/D.  c:
 
== Allmän form (linjens ekvation) ==
s. 113- 115
 
Det kan vara bra att ha sett detta men vi kommer att göra detta avsnitt kursivt och skynda vidare. Det är nämligen dags att göra '''Veckodiagnos 17'''.
 
<ggb_applet width="571" height="319"  version="4.0" ggbBase64="UEsDBBQACAAIACmAaUAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIACmAaUAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1sxVfrjtQ2FP4NT3GUSvxidmLnOjADWpBQkRaKtLSq+s+TeGbMJnGInbkgHqdv0hfrsZ1kkoVCWVA72lnH9sm5fOc7x57l02NZwJ43Sshq5ZEL3wNeZTIX1XbltXozS72nT+4vt1xu+bphsJFNyfTKC42kyFdeuqbBJufJzI8iOguTjT9Lk5jMcC3MUpYkYRR6AEclHlXyNSu5qlnGr7MdL9mVzJi2hnda14/m88PhcNGbupDNdr7dri+OKvcA3azUyuseHqG6yUuHwIpT3yfz319dOfUzUSnNqox7YEJoxZP795YHUeXyAAeR693Ki5KFBzsutjsTU0w9mBuhGgGpeabFnit8dTS1Meuy9qwYq8z+PfcExRCOB7nYi5w3K8+/oAlN05CmAQ3jRZJEkQeyEbzSnTDpjM57dcu94Aen1zxZk4ihlrJYM6MSPn4E6lMfHpqBuIHiEMduy3drfuAG6obQDZGTCd3roRMNnUzoZMLAg71QYl3wlbdhhUIIRbVpMH3DXOlTwa0/3cI5fPIQY1LiAwoHPvLEYY7rvv/QfGP8hmZjPg2SjKzqpv1Go73J0E//vUn6PSaD3iSJPmOSRv8QZfwFcJ0P/yZMEo2QRVP2z34/sRjQb7Do5t9nMA7/kxCX875Sll1xgNoZ2S6TmpfKlEuwgGhhWE8gwtKIEyR5BGSBQ0IBiwFIBGGEU5JCbMYEggQ3QgggBSNHArC1EaX4L0ysshgiVGZWEyxJIGgohCgAYksqBCwksGWJJUoDlIgiiPAlY55QoyKIIYxxFqQQoo+mIhOCggG+iHM0TyEgEJiXSQI0htjoI6Gp9Dg1rqNKCrEPMTEKsaixoF0xo3wKgYkm7uASVd3qCURZmfePWtZDLlAa29G567n2NGmK95YFW/MCz4lrk0mAPStMRVhDG1lp6JMYu7Vtw+qdyNQ11xrfUvCO7dkV0/z4AqVVb9vKZrJSbxqpn8uiLSsFkMnCH3yWBRk908FrnASjjXC8EY024tFz8lm7EnegVRzty0b14izPXxqJc2tAJH+pitOzhrObWoppGMu5PXKWvM0KkQtW/YZkNVYMLtCfQLZb9ScQXcS9I7LJr08KGQzHP3gjV94iMEfuyU1oggfw+IMpVhkz5Rb5Vm40G3+o08/3QxrYkQ8RbhtTvV10ZvJSPZPFecnG+JzVum3sBQH7SmM8v6y2Bbc8sNWLp292s5bHa0eAwOl6e6px5jsH1luLLWD9U3Mibrtx7UYrYzwbpHwr41sJv2eUyId9sqBWwo5rN1oppKhzrYuU9GESvzcjlO1avjepDctvc5a3ldBX/USL7OYcqZF/3ZZrPrBkqpL8IJXL+S0WLW94U/GiIy1mspWtcjU44nPOM1Hi1G10gDCTrF/RAbea823De78Le/VycNldf8zHT5atqheNLF9W+7fIhFsOLOe9l0uVNaI2hIM1NvobfuZULhTDcyIfv2eqDEPPzHmA8GgDDdZfq3eysbcrbBs4WsmyZFUOlT1a3hh+eudWx7BpnC4xGc5d2ep+9dL5171uqrTgJd7JQFuWWqIP+bq0Kk1iQK7fYQu8lc9z4nH7zEjqeG3HjtfAinrHzK2wQ7BgJ95MMLU6X8n8NtKYSAsH9oTaEaXm3FHM+YwPNaqzhTnpaZg6BUdnFE7YpM34wd323XXXRGuK1ZmMx6u3co5EdEB9BbJnd4JsXOT/O1xhB1f0g+CaUvUK29Itpl5ivMRAd5us7MtkNR1uAJZ9BfhRqBOyRsEI+4jcHfozgDPaIRh2CM4IHbQNXVnjpeAGf/gog2QXke8efhZ5zu2F0B1a7yv3inLNkh/rQmRCf8LLY92gPpP9Lui3/KgxJNxYeQ/et1I/pqfZcRav/Ac/Ef8xK4ryrz+ryv66dftW5xRmvKmc+e003gnq6Ul2Z5ztHUvxRmzO95H+wtUj1Inir+BG294IJi+kSwudEnsM4Xzcge1VpvtV/uRvUEsHCIPHZITNBQAAMhAAAFBLAQIUABQACAAIACmAaUDWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAKYBpQIPHZITNBQAAMhAAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAABkBgAAAAA=" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
 
== Ekvationssystem (grafiskt) ==
 
s. 116-119
 
'''Två räta linjer = Ekvationssystem'''
 
Här har vi två ekvationer. Det är ekvationer med x och y. Var och en är en ekvation för en rät linje. De har skrivits på en form där variablerna (x och y) står till vänster och numeriska värdena (siffrorna) till höger.
 
Ekvationerna har döpts med ett nyummer som skrivs inom parentes, (1) och (2). Vi döper ekvationerna för att kunna beskriva hur vi jobbar med dem.
 
Det kallas för ett ekvationssytem:
 
<ggb_applet width="515" height="329"  version="4.0" ggbBase64="UEsDBBQACAAIAFC4a0AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAFC4a0AAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVjrj9M4EP8Mf8UoJ6FDx7ax82qhBXFI6FZaHtJyp9N9cxK3NZvGIXFfiD/+ZuwkTbeAFrij2q7jzHjev/Hszp7t1wVsZd0oXc49NvI9kGWmc1Uu597GLC4m3rOn92dLqZcyrQUsdL0WZu6FxKnyuRfwNJZpzi+iVEwuwjzKLiYiYxfTOFvwIImkn3APYN+ox6V+LdayqUQmr7OVXIsrnQljFa+MqR6Px7vdbtSpGul6OV4u09G+yT1AM8tm7rUPj1HcyaFdYNm577Px36+unPgLVTZGlJn0gFzYqKf37812qsz1DnYqN6u5F/HAg5VUyxX5FIcejImpwoBUMjNqKxs8Othan8268iybKIl+zz1B0bvjQa62Kpf13PNHfML8xE/CKJ4mk2mcRB7oWsnStMysVTruxM22Su6cXHqyKtEyo3WRChIJnz4B97kPj2hhbuG4xLEj+e6dH7iFuyV0S+R4Qnc8dKyh4wkdT4hR2apGpYWcewtRNBhCVS5qTF+/b8yhkNae9sXRffYIfWrUR2QOfKwTF3N87/uP6BvjNyTC+NRJNtBq6s03Ku1VxsHdVfIfURl0KlmYnKvk0Re8jL8SXGfDXdxk0SCyqMr+2O+ZxoB/g0a3/zGFBKSf4OJs3CFl1oIDmhXxtpk0ct0QXIIpRFOqegYRQiNOsMgjYFNcEg4IBmARhBFu2QRiWhMIEiSEEMAEiI8FYLERTfBXmFhhMUQojN4mCElgqCiEKABmIRUCAgksLBGiPECOKIIID5F6xklEEEMY4y6YQIg2EiIThowBHsQ9qucQMAjoMEuAxxCTPBYS0uMJmY4iOcQ+xIwEIqgR0A7MyD+BgLyJ23CpstqYkxBl67x7NLrqc4Hc2I6OXc+1p5OmeG9WiFQWeE9cUyYBtqIgRFhFC10a6JLI3btlLaqVyppraQyeauC92IorYeT+JXI3nW7Lm+myeVtr80IXm3XZAGS68HubdcEGz7y3GjfBgBAOCdGAEA+ek8/q1UiBTSNRv66bjl3k+SVxHFsDRvJNWRx+r6W4qbQ6dWM2tlfOTG6yQuVKlH9hsZIWigt0N5DtVt0NFDDWGaLr/PrQYAXD/h9Za4xjMB35w8/Ug4Mj8SQcTQefCTWmTBD4Iv/0EFIOLSmcnhyaTmKnW277FIm97L1f1oTs1nPaXDa/6+L4yvr/QlRmU9vhATXV5NXzcllIWyMW2XgzZzep3l+74gicrHeHCne+MyBd2rgD9gYe4W25bNfUrZaHLOu5fMvjWw6/qzaV93Q25ZbDrqlbLReWrzOt9ZR1bjK/U6Ma29F87wQ3tvbpnt+Uylx1G6Oym6OnxP96s05lX0GnItl/JHI2vlVhsxtZl7JoCxozudGbxuFzUOu5zNQat47QBkRQsv5EA9zbXC5r2dld2LHMhctS/WGtnr22ol7Wen1Zbt9hJdwyYDburJw1Wa0qKjhI8RK4kceaylUj8A7Jh+cIgeh6RncFhsdQaBCbG7PStZ28sKXgSsAr5BrHLDC2uCjXfZSFnd8onKDT99jUbmXhmC4kf7bOcEhCrUW1EjTjtT4X4iDrkyhYeW8Wi0Ya2CMoCH9zD6fqI/WVzuWtJGBirHuI/4rEU+orKV3RmBYrUKE6C7WTDobJaEiVneUP7foRdfLeyr7qDTbkGxw6sZqigWB6+EPlubSXsWsKH0p3pHHFqNZVoTJlWq0Ie7LXevEre9iWpYv/1zORflcmur7QYf67MxH//4m4OMtE+LMywc8yken1WpQ5lHYUuywNthIMunccD4RP8ADBKDcu8BvTEZ47ea2Us8zaO6BP3fPvSi3Njku3pG65Y26P6fPPUsDbFMRtCnosWIvpLnInk+HbY0vjZwW9r2pMFkW6dead3BusCSTMvQcfNto82f92mHOgDyLiwS/Mf3K42M9DcK/4Q8dlJZ9GEUeiYxCd3K8HclB2X2pXd4fIWRjtMNfIWi2Og4+7vGOvK8KWFf/crs1bCh5Q2P3RJD6ZPphNQjDi7HTysDlhzrBhmMfDZm8nqvafA0//BVBLBwiaXODO+wUAALkQAABQSwECFAAUAAgACABQuGtA1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAFC4a0CaXODO+wUAALkQAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAkgYAAAAA" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
 
Man kan lösa ekvationssystem och få fram vilken punkt som gäller för båda ekvationerna. man kan lösa detta algebraiskt eller grafiskt.
 
Grafisk lösning sid 116 nedre delen, motorcyklar:
 
<ggb_applet width="792" height="457"  version="4.0" ggbBase64="UEsDBBQACAAIADVUbUAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIADVUbUAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVdbb9s2FH5uf8WBnuOYpK4J7BZpgWIB0nZYsmHYGyXRNmtJ1ET6VvTH75CUbDnNit62oglF8vDcvvMdMrOX+7qCrei0VM08oJckANEUqpTNch5szGKSBS9fPJ8thVqKvOOwUF3NzTyIrKQs5wFZsJwKnk6YuGKTKEuiSUbScJLnIluEkQhJVgYAey2vG/WO10K3vBD3xUrU/E4V3DjDK2Pa6+l0t9tdDqYuVbecLpf55V6jAnSz0fOg/7hGdWeHdqETZ4TQ6Z9v77z6iWy04U0hArAhbOSL589mO9mUagc7WZrVPMgIhrEScrnCmBI7mVqhFhPSisLIrdB4dDR1MZu6DZwYb+z+M/8F1TGcAEq5laXoMD+XLA5AdVI0pt+lvZXpcH62lWLnFdkvZyMKwChV5dzqgE+fgBFG4MIO1A8MhyTxW8SvkdAPzA+RH2IvE/njkReNvEzkZaIwgK3UMq/EPFjwSmPOZLPoEK/jXJtDJZw//cIpXnqBMWn5EYVDm0SfZFwn5ML+YGYvoiG7oyDpyKrpNt9odDAZZ+nXm2Q/YjIcTLKnomTxv0SZfCG53oevCZPGI5toyv13P59ZDNk3WPTzHzOYRP9LiLPpwJRZTw7QKyvbI2lErS1dwiuIr2zVU4iRGkmKRR4DvcIhZYBkABpDFOOUZpDYMYUwxY0IQsjAytEQHDfiDH9FqVOWQIzK7GqKlASKhiKIQ6COUhEgkcDREinKQpSIY4jxkDVPmVURJhAlOAsziNBHy8iUomCIB3GO5hmEFEJ7mKbAEkisPhpZpieZdR1VMkgIJNQqRFIjoT2ZUT6D0EaT9OmSTbsxZykq6nL4NKo9YoHS2I5Obc63p7Mu+GxW8VxUeDHcWyQBtryyjHCGFqoxMICY+LVlx9uVLPS9MAZPafjAt/yOG7F/g9J6sO1kC9XoXztlXqtqUzcaoFAVOfqsKjr6ZkevcRKONqLxRjzaSEbf6ZN2Fe7ARgu0rzo9iPOyvLUSp9aAmXzfVIdXneDrVsnzMGZTd8fMxKaoZCl58wcWq7Vi8wLDleO61XDlRGE0OKK68v6gsYJh/5foFPYYFl6S8T/sPge/FWbkbAtvGF1wyz2W2Yv50M/w8knYuaCzJrZHUPheHONddpbLfax2cqtfqeq05CJ+zVuz6dz7AB3qbBw3zbISriocl/HyLda52t/7cgi9rodDaz3yDuRLl2nAbsBi9H7Zj7kfnYz17ChFnAxxEmSoL1ke9+kVcxJuzP3opLBgvWt9pHQIk5LBjNT+JROcMcVVu73KN400d8PEyGJ9itTKv9vUuTjWzLlK+pNUzqaPamq2Fl0jqr6EEcmN2mjPyFF1l6KQNU79Rp8QbsH6HR3wq6VYdmLwu3IvL58ut0vG1fnZslP1plP1bbN9wEp45MBsOng500UnW1twkGPbX4tTTZVSc7w1yvE5yzkMvbC3A6bH2NQgGzdmpTr3uMImgqOlWiVqfFiBccVlsT5mmbsnmk0nqPwDtrFHKJzgwu1TNZLorNKAV+2KWyb1MVf8ILqzLDh97xcLLQzs58GEoYYDjkky2n+rSnHWMXmD0LgAkfOtNWDBb4XwZWN6tkCLBh3ZzroWwqGdsZQ4vvdP94/WPDn5eqx9g414jY9NrKl0pNx+/CLLUrhL2LeGvxt/RPuSFPu2koU0vWUkv/XZRXLPa9Drjj883PzWV6mH48vA5N8FzLgBOJC+GZiox4VdPYkL+6m4hPFjXKL4P8NlnPhC1TVvSmjc0+u2MdhIMMfB6TnAiSUHcGqh8HnemGHjxuvrtXwGpLsBjkjdfBeSlPStmrDvJpmHMk6fRJI+RoPFA0sYokB6RBxE/s89G5W9rfz5dLz6qOmNUz0d9yl3/fd/ur74B1BLBwh3CgwTiQUAAFcPAABQSwECFAAUAAgACAA1VG1A1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIADVUbUB3CgwTiQUAAFcPAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAIAYAAAAA" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
 
=== KevinS - ekvationssystem ===
 
*En film av Matteboken, Bondestam etc
*En Khanlänk
*En text
*En definition
*Ett exempel
*En uppgift
*En bild
*En länk till fler förklaringar
*En länk som knyter ant till matematikens kulturhistoria
*Ett försök att förklara vad man ska ha detta till
 
== Ersättningsmetoden ==
s. 120-122
 
Här finns det plats för Håkan att skriva om annat som ska hända på lektionen än just det som som eleven nedan förbereder.
 
=== PatrikS - Ersättningsmetoden ===
 
== Additionsmetoden ==
s. 123 -126
 
Här finns det plats för Håkan att skriva om annat som ska hända på lektionen än just det som som eleven nedan förbereder.
 
=== RichardS - Additionsmetoden ===
 
Additionsmetoden kan användas för att lösa ett ekvationssystem med två ekvationer och två obekanta variabler x och y. Man måste då eliminera en av de obekanta variaberna genom att multiplicera ekvationerna med lämpliga tal så att antingen x eller y försvinner om man adderar ekvationerna.
 
x + y = 5,
2x − 3y = − 5
Om man vill eliminera x kan man multiplicera den övre ekvationen med -2.Det ger då att − 2x − 2y = − 10
Om man sedan adderar vänsterleden och högerleden får man att − 2x − 2y + 2x − 3y = − 10 − 5
Det ger att − 5y = − 15. Om man löser ut y får man att y = 3. Man kan sedan sätta in detta y i en av de ursprungliga ekvationerna. Om man väljer den första får man att
x + 3 = 5 och det ger att x = 2. Lösningen till ekvationssystemet blir x = 2,y = 3
 
''Wikipedia''


Här är en bra video som visar hur Additionsmetoden fungerar:
[[Diagnos 1 geometri Ma2C]] är en Geogebra som innehåller likformighet, transversalsatsen, randvinkelsatsen, kordasatsen och bisektrissatsen på ett och samma ställe. Jag använder den för att skapa enkla diagnoser. Det är bara att ändra litet i figurerna så blir et nya versioner av diagnosen.
http://www.youtube.com/watch?v=ZIHb8YyeMco


== Lösning till ekvationssystem ==
'''olleh''': http://olleh.se/start/frageprogramMa2.php
s. 127- 128


Här finns det plats för Håkan att skriva om annat som ska hända på lektionen än just det som som eleven nedan förbereder.
'''MalinC''': http://www.malinc.se/math/geometry/circles_angles_proofssv.php
 
=== JakubW - Lösning till ekvationssystem ===
 
== Problemlösning med ekvationssystem ==
 
s. 129-132
 
== Ekvationssystem med tre obekanta ==
s. 133-134
 
== Repetition ==
 
Om du bara vill räkna uppgifter i boken så rekommenderar jag Testet samt de blandade uppgifterna.
 
Kolla att du har en formelsamling. Den är till ovärderligt stor hjälp på provet.
 
=== Räta linjens ekvation  ===
 
* [[Typtal räta linjens ekvation]]. Grundläggande begrepp som lutning och m-värde.
* [http://www.khanacademy.org/exercise/interpreting_linear_equations Khan-övning i att förstå räta linjer.] Den är enkel men det kommer fler med ökande svårighet sedan.
* Häfte med enkla uppgifter på y=kx+m som heter '''Övningsblad räta linjens ekvation'''. Finns bara på min dator. Jag har delat ut det.
* Två sidor med '''Blandade svåra uppgifter på räta linjen'''. Även dessa är från Uppgiftsbanken och (c). Därför finns filen på min dator men kan skrivas ut vid behov.
* [http://www.malinc.se/math/functions/slopesv.php MalinC förklarar Räta linjen] Här finns det '''bra förklaringar''' och en del övningar. jag kan rekommendera fler delar av hemsidan. Sök efter sånt som har med vårt kapitel att göra.
* En laboration om '''knutar på ett snöre''' från sid 109 i boken.
* En '''stencil''' med två räta linjen där du gör en värdetabell, en graf och en ekvation. Tre representationer alltså.
 
=== Ekvationssystem ===
 
* [[Ritpapper för ekvationssystem]]
* Två sidor med '''Blandade svåra uppgifter på ekvationssystem'''. Även dessa är från Uppgiftsbanken och (c). Därför finns filen på min dator men kan skrivas ut vid behov.
* '''Svårare uppgifter''',(c)=hårddisk, räta linjen
* [[Typtal Ekvationssystem]]
 
=== Geometri ===
 
* Uppgift 2239b). Bra att repetera [[Geometri_Ma1C#Trianglar|trianglars]] egenskaper från Ma1C. sidan är stökig för jag måste fixa en mall. Poängen är dock att likbenta trianglar har två vinklar lika.
* Övningar på Geometri, typtal. Den kommer nog inte förrän nästa år :-( Det kan bli något papper med blandade typövningar på geometri som jag ska ta fram mha Khan
* '''Övning:''' [[Förstå randvinkelsatsen]]
 
=== Blandade uppgifter ===
 
* Papper som ska delas ut: '''Övningshäfte Algebra, ekvationssystem och geometri från Åkes mappar - rätt svårt'''. Finns på min dator. Be om en kopia.
* Blandade uppgifter i boken
 
=== Varför? ===
 
När  du repeterar tänker du kanske:
- Vad ska jag ha denna algebra och geometri till?
 
Se filmen så får du svaret;:
<br>
<youtube>Cq832vvq9PE</youtube>
 
== Prov algebra och geometri ==
 
Här kommer en annan typ av test. Mashmallowtestet!
<br>
<youtube>6EjJsPylEOY</youtube>
<br>

Versionen från 28 mars 2013 kl. 09.56

<facelikebutton style="2" showsend="0"></facelikebutton>

Animated construction of Sierpinski Triangle
Animated construction of Sierpinski Triangle

En datauppgift

Inloggning på wikiskola

Ett användarnamn som är ditt exakta förnamn plus Initialen i ditt efternamn

Kunskapskrav

Vi tittar på (ett utdrag ur) kunskapskravet för betyg E i Matematik 2C. Orden beskriva, resonemang och representationer förekommer flera gånger. Det handom att du ska lära dig kommunicera i tal och skrift. Den här övningen är till för att du ska få öva dig på detta och visa vad du kan.

Betyget E

Eleven kan översiktligt beskriva innebörden av centrala begrepp med hjälp av några representationer samt översiktligt beskriva sambanden mellan begreppen. Dessutom växlar eleven med viss säkerhet mellan olika representationer.

Eleven kan föra enkla matematiska resonemang och värdera med enkla omdömen egna och andras resonemang ... ... Dessutom uttrycker sig eleven med viss säkerhet i tal, skrift och handling med inslag av matematiska symboler och andra representationer.

Genom att ge exempel relaterar eleven något i kursens innehåll till dess betydelse inom andra ämnen, yrkesliv, samhällsliv och matematikens kulturhistoria. Dessutom kan eleven föra enkla resonemang om exemplens relevans.

Eleverna bygger sidorna

Syfte

Eleverna ska lära känna ett begrepp ordentligt. Eleven ska höra talas om andra begrepp genom att kamraterna jobbar med dem.

Vad ska varje elev göra?

Varje elev ska göra ett avsnitt på denna sida. Avsnittet ska innehålla text, bild, film, länkar mm som ger en ökad förståelse av begreppet. Det kan vara sånt som jag brukar ha med: Khan, Mikael Bondestam, Wikipedialänkar, GeoGebra, osv.

En bit var

Jag läste igenom kapitlet i min matematikbok och markerade 16 olika teoribitar som som verkade bra att jobba med. Det blir en per elv i klassen. Jag valde sådana bitar som är hyggligt enkla att förklara, lätta att hitta information till och viktiga att lära sig. Sedan skrv jag in eleven namn och hens begrepp som rubriker på denna sida.

Innehållsdelar

Nedan en lista innehållsdelar som kan vara med i ett avsnitt. Allt måste inte vara med.

  • En text som förklarar begreppet (obligatoriskt)
  • En film av Matteboken, Bondestam etc
  • En Khanlänk
  • En definition
  • Ett exempel
  • En uppgift
  • En bild. Helst från Wikimedia Commons
  • En länk till fler förklaringar
  • En länk som knyter an till matematikens kulturhistoria
  • Ett försök att förklara vad man ska ha detta till

Bedömningskriterier

Så här ser bedömningskriterierna ut när de saxats ur Skolverkets kursplan. jag har klippt ut det som är relevant men det återstår att skriva om och tolka kraven så att de uttrycker konkret vad som krävs i just detta projekt.

För betyg E fordras

Innehåll enligt minst sex av punkterna ovan. Innehållet ska vara korrekt och relevant. Texten ska vara välformulerad.

Eleven kan översiktligt beskriva innebörden av centrala begrepp med hjälp av några representationer.

Dessutom uttrycker sig eleven med viss säkerhet i tal, skrift och handling med inslag av matematiska symboler och andra representationer.

Dessutom kan eleven föra enkla resonemang om exemplens relevans.

För betyg C fordras

Åtta av punkterna ovan.

Eleven kan utförligt beskriva innebörden av centrala begrepp med hjälp av några representationer.

Dessutom uttrycker sig eleven med viss säkerhet i tal, skrift och handling samt använder matematiska symboler och andra representationer med viss anpassning till syfte och situation.

Genom att ge exempel relaterar eleven något i några av kursens delområden till dess betydelse inom andra ämnen, yrkesliv, samhällsliv och matematikens kulturhistoria. Dessutom kan eleven föra välgrundade resonemang om exemplens relevans.

För betyg A fordras

Eleven kan utförligt beskriva innebörden av centrala begrepp med hjälp av flera representationer.

Dessutom uttrycker sig eleven med säkerhet i tal, skrift och i handling samt använder matematiska symboler och andra representationer med god anpassning till syfte och situation.

Genom att ge exempel relaterar eleven något i några av kursens delområden till dess betydelse inom andra ämnen, yrkesliv, samhällsliv och matematikens kulturhistoria. Dessutom kan eleven föra välgrundade och nyanserade resonemang om exemplens relevans.

Editering

Editera under er egen rubrik. Inget kan gå fel. Allt går att rädda.

Titta på färdiga sidor hur man kan göra och härma wikikoden.

Läs mer om Wikimarkup och hur man editerar.

Milstolpe

Ditt arbete ska vara färdigt för bedömning måndagen den 12 mars.

Vinklar

Ma2C: Vinklar, sidan 66-70
Load video
YouTube

Genomgång

Vinkelsumman och yttervinkeln finns visade på Geogebra.se

Definition: Vinkelsumma 

Vinkelsumman i en triangel är 180o

Definition: Sidovinklar

Sidovinklarna är tillsammans 180o.


Definition: Vertikalvinklar

De två vinklarna är vertikalvinklar.

Definition: Alternatvinklar

De två vinklarna är alternatvinklar.

GeoGebra om Alternatvinklar mm.

Sats: Yttervinkelsatsen

Yttervinkel till triangeln.
Yttervnkeln är lika stor som summan av de två motstående inre vinklarna.
 γ = α+ β

Bevis: Yttervinkelsatsen

Länkar

Malin Christersson har en fin sajt där jag hittade en Geogebra om yttervinklar: http://www.malinc.se/math/basicgeometry/exterioranglesv.php

Likformighet och kongruens

s. 71 -74

Khan Academy: likformiga trianglar

AmmarA - Likformighet

Alla figurer av samma färg är likformiga.


Definition

Likfromighet är två objekter som har exakt samma form, men är inte lika stora (se bild ⇒⇒).


Två trianglar är likformiga om något av följande är uppfyllt: 

VVV: Motsvarande vinklar är lika.
SSS: Förhållandet mellan de tre sidparen är lika
SVS: Förhållandet mellan två sidpar är lika och mellanliggande vinkel är samma

Video

Load video
YouTube

Exempel (Uppgift)


Exempel
Formeln

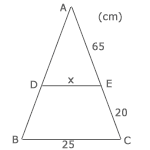
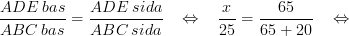
ADE bas/ABC bas betyder att vi tar måtten på sträcken DE från den lilla triangeln och dela den med måtten på sträcken BC från den stora triangeln samt ADE sida/ABC sida betyder att vi tar måtten på sträcken AE från den lilla triangeln och dela den med sträcken AC från den stora triangeln, och det blir alltså summan på AE och EC. Man kan också använda formeln genom att dela den stora triangeln med den lilla istället, och svaret blir detsamma.

Svaret

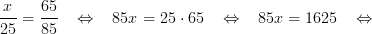
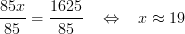
Användningsområden

Man kan tex. använda likformighet i avbildningar när man ska rita kartor och jorden på olika skalor, dvs. 1:2, exempelvis:-

Bilden från Wikimedia Commons

Hund i längdskala 1:1

Bilden från Wikimedia Commons

Hund i längdskala 1:2. Areaskalan är 1:4

Länkar

Topptriangelsatsen

Den här filmen handlar om likformighet och topptriangelsatsen. Observera att sidan som är 15 lång i exemplet gäller sidan på hela den stora triangeln.

Load video
YouTube

Kongruens

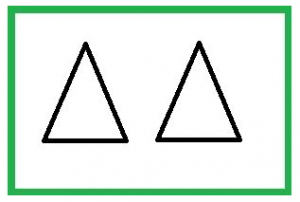
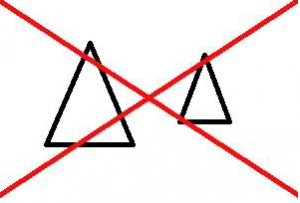
konguenta - samma form och lika stora
Icke-kongruenta - olika storlek
Definition
Kongruens

Två figurer är kongruenta om de har samma form och samma storlek.

Två trianglar är kongruenta om något av följande tre fall gäller:

  1. Två sidor och mellanliggande vinkel (SVS = Sida-Vinkel-Sida)
  2. De tre sidorna (SSS = Sida-Sida-Sida)
  3. Två vinklar och mellanliggande sida (VSV = Vinkel-Sida-Vinkel)


Länkar

Bilder

Extrauppgift på kul

kan du rita en sån här? <ggb_applet width="681" height="450" version="4.0" ggbBase64="UEsDBBQACAAIAIOsdkAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAIOsdkAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7VpZb9tIEn7O/IoGnyOpb5KBnIHjxNkAmQNwdrHYlwFFtqgeU6SWpGQ5mB8/1d2kROpILDsxPIGNKH0Vu7qOr6pa1Pjn9TxDK1VWusjPPDLEHlJ5XCQ6T8+8ZT0dBN7Pr38ap6pI1aSM0LQo51F95nFDqZMzT04mVDDBBn4QsAFnQgwmTMqBP+WRmiR0gmPqIbSu9Ku8+DWaq2oRxeoqnql59LGIo9oyntX14tVodHNzM2xZDYsyHaXpZLiuEg/BMfPqzGs6r2C73kM3zJJTjMnov798dNsPdF7VUR4rDxkRlvr1Ty/GNzpPiht0o5N6BqcPQg/NlE5nIJMIhIdGhmgBClmouNYrVcGjnaGVuZ4vPEsW5Wb9heuhbCOOhxK90okqzzw8pIxJn4SgniAIZShAHUWpVV43xKRhOmq3G6+0unH7mp5lyT1UF0U2icyW6K+/EMUUo5emIa6h0EjplrCbw8w11DXcNcLRcPc4d6Tc0XBHw5mHVrrSk0ydedMoq0CFOp+WYL7NuKpvM2XP00xsxScvQaZKfwZihsFPnM5hHuOX5iPhw83CqC8k6XCty+WJTFuWgoi7s6QPYclalkSSfZZUHJFSfkG57gx3EZOIjmaBlf1nP3scGT2Boxs/jKHkjyLieNQiZdyAA1UzQ9tYslbzysCFhUiExusJEgAN6YOTC0RCaHyKAAyICMQFDEmApGl9xHxY4IihABk6wpDFhgjgP+7bzSQSsJmZ9QGSiAAjjgRDxEKKIwASsrAEiFIGFEIgAQ8Z9oSaLZhEXMKIBYjDGQ0ifQKEDB6EMbCniBHEzMPER1QiafYj3CBdBubosCVFEiNJzIYAagC0AzPQB4gZaWSjLp0vlnVPRfE8abt1sdjYAqghHG2jngtPvaD4YpxFE5VBnrgylkRoFWUGEZbRtMhr1BqRurm0jBYzHVdXqq7hqQr9Ga2ij1Gt1pdAXbW8LW1c5NXvZVFfFNlynlcIxUWGN2cuMtLp082pYcA6C7y7IDoLstP3D/ItYAUtKwX8i7JqyaMk+WAotqEBNPlbnt2+KVV0vSh0X4zxyKacsVrGmU50lP8HnNVwMXpBbQay0arNQJzR9iBFmVzdVuDBaP0/VRagx5AMw+6fh27dChW0vwLoq+LIYI+H/RUDzNsja4F0vNVqY6JorbbSpqWBdmfwoXpTZNspq4CLaFEvS1s9QHQsjVjneZop6yQW2pCa4+tJsb5y3sHcXp9uFzDC7gST1CoelUY2UE/atBPXWhpztA0VtjTYUuDW3XSyWSchtRS2nbjWUoH/uqM1opJWTIJbNrqyIQ17DXDacGW832T6Za7rj+2g1vH1VlTzwK/L+URtfKi/J/lWe45HO042vlZlrrLGp8GYy2JZOYh23D1RsZ7D0C00KomMuf4NB3CziUpL1R48s5WZU5hdxV133Zu2W12WxfxDvvoEvrBzgPGoPeW4iku9MD6HJpAHrtXWqxJdRZBGku5zBoQgemzSBainNqoBeC7rWVHa4guiCrQGe5maQ6WFaute1kM3aj63NZzRJyomf0Jg2+Q+t741GCwfdDXrlFG2mEWmzmuEzqJbVfbUYPf7pUh2lQO6txIAyhfOtgulnFu480JnAdtZNPWiFGi7Quszb4CHMgBEG/am89mV8K6GNcIakPUis5vdsRS4j9PTVzT25p+vMTIkvFGYz7+JwuJiPo/yBOW2uLnQZZwpb5ttI2w8DUXEqM/pZlm3C7HbrNliT/vg5zreaDf+ivY78h5TP76/8reRsoYsfg03lcpWz3UTuG3nXzpJlK3gXCbRqcpXcFJIonAFxM0F8xY7/uhzO7Mm1pfNGmmmPpOOacDspV6j85b+vKU6h+w/oEMWEtLJZOBj56zhcc5bcJyLFjDucP/PnTyVi62mttFTHd/Dvm+cfc/37JucYt/k2b6H7UuGXAZ+v/Tp2XfgUN0YGHD9AAN/yGtIrSDTjo1jZ+MEGrpRQMfUF182dT+QXtwrkJriLXXNxDX3NfY2HuIh8QPMAu4L36chY1La8EiHNJBESsp4EPjSD9hjBcuLY2BSp4BJPYPpIJjgDsEpFcwXlIUSC7YbKwcHPcJC64BPfAegJc7+ygGN7rnB21OA9vbJAM1c3npq9RucMd7T6aMVJW+dni/2FDw9BWfTZ5wdxJkckgDLLc7oHs4OOUQDsz2X+H4wmx6D2btTYPbuycCMDkPR+1ZDNNX+t7kd3QFX744V++kpuEqfcXUEVzgQ4gu1/uCQBzSV4YMq/7sVhvtAujwFSJdPBkgYkj0JJREU6gUfQziyQDJalL3oRB8LWJfHCsPZKcCaPQPr2C2aB7JTGVK5Xxnuu4RB1gGX+H4JKz2Gs/en4Oz9k8EZHRLcVaq/gRnu6tQPHwtm74/lr+tTYHb9DLMj9y/AF+GScl9iFvLA389few7RgGzXIR4Ast+L7DYt8sMR9r2DmClkmLsncHctF4eib7MVaerJP4h7OrUdeF7ZDuyQ2A7sEduOPPOir0HWHbL1mQ2n+5r4ZHckglmHFGTPI8kpHnn8C/ZKpWa0Pcgf5H7I+cJR7x2bjJdL3P2jvqunyTCgvQW/CU8CLjIcUxaEPCRhED4AjzuOreeLTMe63jhgZr7m32QLXeT7L7iulVqYN4u/5Z/KKK/Mj5ccTefF2R0Nkz4pw5Ch7EWD9iVQILpXSuqswsGKkJQJ9bkEqwQ/jE3UE7OJ4LtfmbpUDtG8E9CFu4oKc82nP6BVkqdklb0Ihl0AG5gI1qCDCEy2MevHCVnxUzLEXsTa3ifF7tdgNpNIX0gRUswoDymR/IcxS/SUjLITskiTR/oRS7qXP3jIQp92bELEP8goo+6vRuyvs5ofGr/+G1BLBwi7UrqBaAgAAAUtAABQSwECFAAUAAgACACDrHZA1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAIOsdkC7UrqBaAgAAAUtAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAA/wgAAAAA" showResetIcon = "false" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

Längd, area och volymskala

Förra veckodiagnosen ?

s. 75- 79

Tisdag v 8.

Håkans tips

  • klippa in en svg-bild fr Wikipedias source

Definition 

 Skala =  En sträcka i bilden / Motsvarande sträcka i verkligheten

Definition: Längdskala 

 Längdskala = Bildens längd / Motsvarande längd i verkligheten

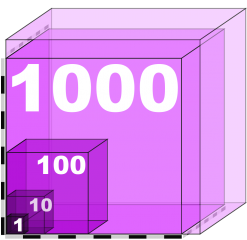
Definition: Areaskala 

 Areaskala = Stor kvadratens area / Lilla kvadratens area

Definition: Volymskala 

 Volymskala = Stora kubens volym / Lilla kubens volym

Länkar

ViktorE Skala

Topptriangel- och transversalsatsen

Topptriangelsatsen
Transversalsatsen

Wikipedia skriver om Topptriangelsatsen Wikipedia skriver om Transversalsatsen

Det finns en PPT som förklararar dessa satser och ur de hänger ihop: http://wikiskola.se/index.php?title=Fil:Likformigheter_och_transversaler.pptx . Det är en kort ppt så dess bilder finns med här.

NilsG Topptriangelsatsen

Ma2C: Topptrinagelsatsen, sidan 81- 85


MalinC Brättar om topptriangelsatsen

Load video
YouTube

Transversalsatsen


<ggb_applet width="796" height="336" version="4.0" ggbBase64="UEsDBBQACAgIAPu7VUAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAD7u1VAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1a2ZLbNhZ9dr4CpYd5mUjCDsKjdspbKq5ylqr2TE3NyxQlQhLTFKmQVC+p/E6+ZH5sDgBSq+3u9pK002U1SOIS9+Kcu0HtyTfXq4JcurrJq/JswEZ0QFw5q7K8XJwNNu18mAy+efLVZOGqhZvWKZlX9SptzwbSS+bZ2cCYuRaap0Mt0/lQ8mw+tEa54XzK05nTZiaT+YCQ6yZ/XFY/pCvXrPH8fLZ0q/R1NUvboHjZtuvH4/HV1dWoVzWq6sV4sZiOrptsQGBm2ZwNuovHWO7gpSsRxDmlbPzv71/H5Yd52bRpOXMD4rewyZ989WhylZdZdUWu8qxdng0SKgdk6fLF0u/JsAEZe6E1AFm7WZtfugav7t2GPber9SCIpaWffxSvSLHdzoBk+WWeufpsQEfCWq6EEUxIwROhzIBUde7KthPulY775SaXubuK6/qroBJmtlVVTFO/JPntN8Ipp+RrP7A4cAxaxykan1ERBx4HGQcVZWR8XUZRGWVklJFiQC7zJp8W7mwwT4sGEOblvAZ92/umvSlcsKd7sNs++xp7avJfIcwo/CRiHm6+9h+Nj/QT48NNsj2tbb25p9JepTT3UMk/RqXoVQrOTlVy9Y5d6veAG224yzaZ2tsmVIV/4XOiUfB7aIz3tykUiVdoEvlWhVr+IVucjPtImXTBQZqll+2YbN2q8eEiLFHWez0jCqGhDZxcEWYxGE4QDIQpIhVuWUK0Hw0RBhOSCJIQL8cECbGhEvySJiymicJi/qlBSBIGRZIoQVgIKUkQSCSEJUKUC0goRRRe8uoZ90sITaTGnUiIhI0+Ig2DoMCLuId6TgQjwr/MDOGaaL8ekz7SdeJNx5KcaEo08wsiqBHQMZghnxDhd6M7uPJyvWkPIJqtsv6yrdZbLiCNdLTLejE9HSTFR5MinboCdeLcM0nIZVr4iAiK5lXZkp5EHp8t6nS9zGfNuWtbvNWQn9PL9HXauutvId30uoPsrCqbn+qqfV4Vm1XZEDKrCrq1uSrY3jXfWo0bsTch9yfU3oTeuzZv1VthhmwaB/1V3fTiaZa98hK71AAkfyyLm2e1Sy/WVX64jck4lJyJ28yKPMvT8l9wVq/F40L6ChSyVV+BBEt6Q6o6O79p4MHk+j+urjBHR1xQavAjFVWJRR25iVM80SONUiYox+/EUJ+YZqkPPm5HzEjGE8OUMlxohbf6uZFNLE14YoVMEsl11O0utxSl126320XtQ3vv5lXzrCp2jwIAz9N1u6lD9wAjar+tp+WicMFJQmijNM8uptX1efQOEdd6c7PGHY0WTBcBeILkwH2BXnTjFKNSUcabtpWiQYYGCdq7W55t55nlQSKM0zgGKfhvNK3bKuu3yWivJm9CSqODLnD6dOW931f6TZm3r/ubNp9d7LbqX/hhs5q6rQ8drsk+1ZqT8ZGTTS5cXbqi82mQuak2TQzRPXfP3Cxf4TZOdJCknq5/woD4NHOL2vWGF6Ezi4CFWbrvriePw1Lf1tXqVXn5Br5wZMBk3Fs5aWZ1vvY+R6aoAxdu51VZ3qQoI9n+ez4IsfWZLxeAp/XQIDw37bIC2d/97/eLtCQvC/RfTZsvsAayDCR8LBZuhc6LtMHdgsduYX8aejqPL6mmPyPRbWthnN8RiOm3up53TpIW62Xq+74OhCK9cfUBLGG976vsGCxwEXaEqF/7BTzba+eio0SLcbHGgiG+DvIW8G/Ite/LJaOIaqUNek7p/f0GtXNEubUW7R0VqJ7IMuTX2O3Hdtfj4OPxIInHp0ekwtMihLeA+exhgfkhUDJo5UmSsIRzrQW3MmDJ1EgIyRSaecV9U//ZsXz+5WNpRowrzaWyOkErzk2A0tiREYoZPFJGWP1JkJxVq1VaZqQMzeZPVXGzqMrBrv1JqQ91kjLvpCTlHt8I3qbt57u3WBSbRbEUA/qLaVTYqXkLdVFhT852qcNy06IVusBxrwlHkLarfuHiuzzLXGiDx+/nfQ/pfeKZEoF6xbp6uGOe3Yf5d7tn4xb+bmvI7BYHvb+h93TRnaMNEbUCh1ot0NEgdgUXXQbUzFgLL1T4JJRHX4NfWk6ttgZNEDVMHrcFd+fJ/VLGV5pYq/PVushnebt1rsLHx6uyRVVyoXSdFuQL59a+E/qxfFOnZeO/bIkye4X+jpykD4gTjapEGeUS7alCwxmjf4j+kyKJGu4JEcixJpCiLShMLPIFY8Jaw/4ynEwfDidGjgxVDBGiFcBWtqcEMWCERLsgQIvwdQOUDAWqXqJ9NGlqkcZP2ucHzMlxQfCl9bAcTE8KwIvbkvx+fX7xQfUZaSieSfz4MJpHNZIWZ0VBhTbwAqODUwg5SpBNheKGWTRCn6FKv4YfHXHyoq+9x9Rk76fGu+QW+ezDAu7wOPmHV6Uh0t6IMVQmg9woeMLF5wm3dxOyDb8jVrLISnrCysv7BMzLDwoYHb8J0PGLAD98PDFC+kQIj/d+ryzgjj2+pobD6yXiAC2+pdHphWUQRvtqZSJ0wrX6hDFw3hWLQ8CfR8BfnAA+fz/gx6Vn/tFniE8SCBK5xGohBX6METEKhmykUWAoU5oyBlRZV3VYYkdAWXL/tRf6BjQIX2rZeTu7XZJ7esKuux+77mGwy0EXRYZDdDDNNE9kzy9NkPK41L7ZThLZ0cv1iAqJ6FKCQ1x9pjT3p9H7LNL78oTexf3oXTwMeocc9Qo5MvEHeJQsybf8MpVIpa3UXCQ+pwaCuUFDgYOV5Examyj5Vwvfl5Hf0+8Plvfjd/lA+BUJDgXCSIlQ5GovfPEokG6VlpbZWA0lkyPLqK+PGsc7pvUXRK+7XtcwzHfMHcgXl1X7X7TImMGyZEy6v4MdUlduVq7OZ4Ojt7x+6Np00LKRopqh39PWotbpxNydPnZHU3ln6hKmLu5sKr/V1E9q6Rt33faY/u2XTdX+Yz52Z/GK/J30mJ8a3+LFweEqf2Yr37Rp3YajIwlt40gwg4TnQ0LiPGxViBSdID8qSgXFIdoqcXBUuh0ofgDUcrw4AorfCSj+kIDCuYehczNGaZR4RXk8UmoDoOBzOPpIiVNl8i6gxvt/6gl/Uu3+d9CT/wNQSwcI4u9Zvw0JAAC6JAAAUEsBAhQAFAAICAgA+7tVQEXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICAD7u1VA4u9Zvw0JAAC6JAAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAKUJAAAAAA==" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

Euklidiskt bevis av Transversalsatsen

Uppgift
Bevisa Transversalsatsen

Gå till sidan MalinC om Transversalsatsen och följ hennes instruktion om hur du bevisar transversalsatsen.

här får du göra det "Euklidiska" beviset som bygger på jämförande av areor. Detta är en uppgift på C-A-nivå


Randvinklar och medelpunktsvinklar

86-91

Onsdag v 8.

Vi har en kort lektion för tre tunga geometriska satser. Så ser grovplaneringen ut och vi måste komma vidare till avsnittet om räta linjen. Det säger sig självt att vi kommer att behandla detta översiktligt (inte så noga alltså). men vi kommer att repetera detta när ni har lagt in ert material. Ni kommer inte undan er uppgift att skriva på wikiskola för det där med att kommunicera matematik är ett viktigt grundmaål.

Även om dessa satser är intressanta är det inte centrala. titta på beskrivningen av det cerntrala innehållet i geometrin: 

  Användning av grundläggande klassiska satser i geometri om likformighet, kongruens och vinklar.

Med klassiska satser om vinklar menas förmodligen vinkelsumman och yttervinkelsatsen tillsammans med begreppen sidovinklar, vertikalvinklar och alternatvinklar (och transversalen). Jag ska titta i en annan bok hur de tolkar kursplanen.

Nåväl, något måste vi göra och min idé är att vi tar GeoGebra och konstruerar alla tre geometriska figurer och sätter oss in i vad de betyder på detta sätt. På det viset kommer vi att prata om och jobba med begreppen och det ökar chansen att vi blir bekanta med varandra.

Håkans tips

  • bädda in youtube. Det kan vi göra med Nils film ovan.

Extramatten

Extramatten idag handlar om att repetera inför omprovet

DenisJ - Randvinkelsatsen

Här kommer ett riktigt bra bevis av randvinkelsatsen:

Load video
YouTube

Och därefter kommer en film med Kahn:

Load video
YouTube

Ett uppgift på Khanacademy för Randvinkelsatsenm

Håkans GeoGebra om randvinkelsatsen

<ggb_applet width="554" height="521" version="4.0" ggbBase64="UEsDBBQACAgIADa5VUAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIADa5VUAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vrbcts4En3OfAWKzxGFO8CUnCnFuWxqM5OpcXZra98oEpI4pkgtSdlyan5q5/Ib803TAEhdLPmixEmUuBJTJJpodJ8+3Q3Ig++XsxxdmKrOyuIkICEOkCmSMs2KyUmwaMY9HXz/9LvBxJQTM6piNC6rWdycBNxKZulJME5HIxpT1Rtxk/S4lqoXjcakp7WUOkqNZglIomWdPSnKH+OZqedxYs6SqZnFb8okbpziadPMn/T7l5eXYacqLKtJfzIZhcs6DRAss6hPgvbDE5hu66VL5sQpxqT/nx/e+Ol7WVE3cZGYAFkTFtnT7x4NLrMiLS/RZZY205NASBqgqckmU7BJKhKgvhWag0PmJmmyC1PDqxu3zuZmNg+cWFzY8Uf+E8pX5gQozS6y1FQnAQ65IJFQNBJMMSkFVwEqq8wUTSvcKe130w0uMnPp57WfnEoeoKYs81Fsp0S//ooophg9thfiLxQuUvoh7J9h5i/UX7i/CC/D/evci3Ivw70MZwG6yOpslBtAOM5rcGFWjCuAb3VfN1e5cetpH6zNJ4/Bpjp7D8KgL0De57Dwx/gxx+6/t3nDQLKhsakWByrs1AnB76eOfpSB7Ebz6E3myVsUenvvYx8RG/oEfuz+uf87GtltJl7X6O/vUsi0Vag036tQ8s9i4qDf0WPQMgLVUyvbRk1jZrXlCIuQiGyoEySAD1JBZAtEIrgoioABiAjEBdwSjaS9KsQUDHDEkEZWjjDkCCE0/OLKTSaRgMnsUwU8RAQUcSQYIo5HHAF7kOMi8JIykBACCXjJqifUTsEk4hLumEYc1mhpqAgIMngR7kE9RYwgZl8mClGJpJ2PcEtvqe3SYUqKJEaS2AmBycBiz2CQ14hZa2TrrqyYL5otFyWztPvYlPMVFiANOWid6nxO2sqEjwZ5PDI5FIcziyRCF3Fu2eAUjcuiQR2I2j+bVPF8miX1mWkaeKtGv8QX8Zu4McuXIF13up1sUhb1T1XZnJb5YlbUCCVljldrLnOy8ZmuVg03bGOAbw6IjQG58Vnt1VvCCFrUBvSXVd2Jx2n62kqs0wJ48m2RXz2rTHw+L7NtMwZ9V2cGZpHkWZrFxb8hWK0W6xe0Kjs2TXVlh0esW0hZpWdXNUQwWv7XVCX4kYSMac1ppATFUgToyg8wpkIGWVtTHnEmuYKqUiexpR6HdyhlhGMeCajHEAhXNwwpr9hcrPCJl2Zt6qRyFX5987p+VubrR87603jeLCrXL0BarKxNw2KSGxchjtdQjJPzUbk886HB/FzvruZwh/0KRhPndQSZgQqwctJeR/7qZOzSVlLYyWAngbtYy9LVOImok3DXkb86KQhev7TWVNKZSXCnJqtdPsNBy5ouV9nQt7V9UWTNm+6myZLztan2hR8Xs5FZBdD2nOSh5hz0r0XY4NxUhcnbgAYwF+Wi9vzciPXUJNkMbv1AZ7GF61+wAP80NZPKdAvPXS/mHbb5jo/VncduqpdVOXtdXLyDWLi2gEG/W+WgTqpsbmMOjaAInJt1VKVZHUMNSTffswwE0xNbK8A9jXUNcHPRTEsA+8zMsiKussUM/RNyS1rBe/V5mccFzAYPQNZSMjcz6LpQ4wLPxe4KgKHr56ynUTn6BfLdqiT68TWUMLw3CF24xvl8Gtuer3VHHl+ZastBbr4fyvS62wAVZxuQf24nsLjPjfEh07RUQXOY0DFtK30BEjVaQgEOCQT7FawltMX/ve/nfUNrrbX828rY/uk1ECGyvKPucNmzXZdtB/XGGo/YaTSUzmcipPJBfJaUs1lcpKhwfc9pViW5CdaFOMY22lBMrAe9cxZNN5D4ydopdgAAFmTJyr/JHTF7D//jD/f+Oo82UODPYedSu6565Xb74R9ZmhrX3Pk6k01McQErhfoKW0LcbjivsNeP3ndPluCdnnt0RdpH78kGNIB7lS3RsJMfdlJDaAwoCTWmGm5YO+8QuoKeZ8cQeoKe44df0f8Kb0Tt063tdbJxltwO6k+OCNuYJjtgnt4O5jabTj8oARHqa6W7HgefGLiZM0wYrIXJCNtOx9FLRVRRrIRkmkXqE1Dtfqg8PwSV598KKjxUmEUR1ZoqzHVbJ4AI0EJSIrjilGusbIP54LicmYl9fg2ZU58Dn+8AFN8OUN3O1kEQf9EsuPawCjWDTl5ShiWjmPuqQkKhIhkRIRSRKsJ2jwwO7jEWShpxwhSlShCtPiKpXkth2WyeZ0nWrByb27h4XTTQPxrXQO22hefGzG0//rZ4V8VFbQ/5vMxGu/lRrHtxCOtefCus0yGRWOGIYQwbOCW1Zx0JlVZUYAapMMKci0/ReNzKuhc7AI0OY93oaFgH/IoUIRRTxTkRbbEB33KsIsWVxFoyTzpBQy2kJFozIkmkd3aEXw3p9oP7woM73AE3PQzc9EjA7fGQ4C2irKvWJq2U5w+NQq2wJkpjpjBmXH9j+A5vKpnmMHzNkeDLQyiXm91Hlx45pE0MpLZfmgBb/V62RxkMEPtGBGRnLPpq4XXnY9fAfe7BtQma7kvQf/3/dpDdycsKQpC278N6Fp33Q6aVAMdBqoQ2RHenah925kHwbhyQW+Pg7Xhcm8bCbg8ALc58b5SQD0c1rpKNqtlV8jwvL38249wsndsfAKPhjRj9dhBGv+1ipAAi2DJRjgmkNvKlIKK+UzluhO7Xeb48pPN8edeZ1lfTeqqQatiLQGaFQIL6SbrSSWAvQgXUTiLh96fY79kjr8UscQdfwyrZz6GXN3FofI8jsHlcrTEbf1g1675m8CQR5IFPwqLjOQmDBrn7ueNMDG/8cHYUpfJ+JH91CMlffSvbSwJ6NRFMUCkotMH+UIeHkmEd2RMHaJc40Z9tc/nqpv50clh/OjmS/lSGUjFCCIYduoh45E8yeyJkUKY5ZZqCjyPsHdzjwCBFmVSEERZxJr7a9vTW3eWrHXSnh6E7PRJ0IfkBOQi3VRCqoZZMtEd2EcUAbSR5pIBH1NdIISCXRpK6xkwK/E3uPl7d2Nn+flBn+/vduw/5pXrbyH9Fuj9KjqW33YfRiy2MdrPsX38chNEf1zGCAI+EtJEvCOQ9vG/3cZ9u+OYveO+9/Wh3iOyrBWl4I0h/HgTSn7sgCXvEFbkzTCnJXh59HpR6MmphYkcGU3/zz0Xc32S1f1P89G9QSwcImk/H6UcJAADwLAAAUEsBAhQAFAAICAgANrlVQNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICAA2uVVAmk/H6UcJAADwLAAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAN4JAAAAAA==" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

Öva

Öva på Khan: Randvinkelsatsen


Bisektrissatsen

Load video
YouTube
Bisektrissatsen


Länkar 


Text om Bisektrissatsen.....

Defenition...

Bisektrissatsen = AD / BD = AC / BC

AntonL - Kordasatsen

Antons hittade film:

Load video
YouTube

Repetition och sammanfattning av geometrin

Diagnos 1 geometri Ma2C är en Geogebra som innehåller likformighet, transversalsatsen, randvinkelsatsen, kordasatsen och bisektrissatsen på ett och samma ställe. Jag använder den för att skapa enkla diagnoser. Det är bara att ändra litet i figurerna så blir et nya versioner av diagnosen.

olleh: http://olleh.se/start/frageprogramMa2.php

MalinC: http://www.malinc.se/math/geometry/circles_angles_proofssv.php

Hämtad från ”https://wikiskola.se/index.php?title=Geometri_2C&oldid=21930”