Konjugatregeln: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Wedrawde (diskussion | bidrag) m (→Konjugatregeln) |
Wedrawde (diskussion | bidrag) m (→Konjugatregeln) |
||
| Rad 5: | Rad 5: | ||
a<sup>2</sup>-b<sup>2</sup> = (a-b)(a+b) | a<sup>2</sup>-b<sup>2</sup> = (a-b)(a+b) | ||
utför multiplikationen | utför multiplikationen: | ||
(a-b)(a+b) | |||
(a - b)(a + b) | |||
= a<sup>2</sup> + ab - ba - b<sup>2</sup> | |||
= a<sup>2</sup> - b<sup>2</sup> | |||
V.S.B. | V.S.B. | ||
Versionen från 3 mars 2013 kl. 17.14
Konjugatregeln
Så här ser den ut: a2-b2 = (a-b)(a+b) utför multiplikationen: (a - b)(a + b) = a2 + ab - ba - b2 = a2 - b2 V.S.B.
Konjugatregeln med <math> [math]\displaystyle{ \LaTeX }[/math] </math>
Så här ser den ut:
[math]\displaystyle{ (a-b)\cdot(a+b) \\
= a^2 +a\cdot b -a\cdot b -b^2 \\
= a^2-b^2 }[/math]
[math]\displaystyle{ \blacsquare }[/math]
Länkar:
- engelska Wikipedia
- På följande sida finns en bra sammanfattning av konjugat- och kvadreringsreglerna med bilder och exempel.
Film
Bondestam (tv) respektive Matteboken (th) förklarar:
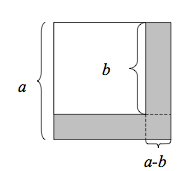
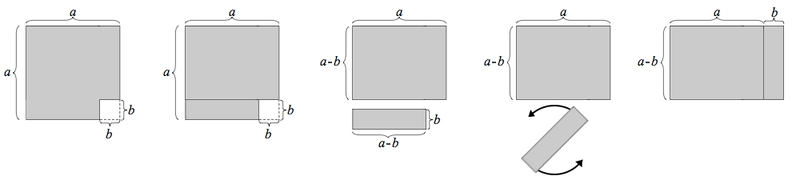
Geometriskt bevis av konjugatregeln
Första beviset
Andra beviset
Uppgifter
Webbmatte