Algebra Ma3C

Lektion 1 Geometriskt bevis

Uppgift

Ni ska göra en ppt och förklara de fyra geometriska bevisen. Det kommer att vara CC och ni jobbar gruppvis två och tvås eller tre. Det kommer att publiceras. Ni börjar alla på papper och sedan gör ni ett som vi kommer överens om i presentationen. För att lyckas kan ni behöva läsa sidan 54 i boken eller gå tillbaks till Ma2C länk... Exempel på förklarande ppt: Multiplikation genom uppdelning av talen Här ska ni jobba alla tillsammans på en presentation i Google Drive. Klicka och börja jobba här Presentationen är för tillfälet stängd för redigering för att undvika klotter. --Håkan Elderstig 21 oktober 2012 kl. 12.25 (UTC)

Resultatet ser du här till vänster.

'

'

Repetition -Algebra

Här kan du repetera kvadreringsreglerna genom at expandera fönstret nedan:

Första och andra kvadreringsreglerna

(a+b)² = a² + 2ab + b²

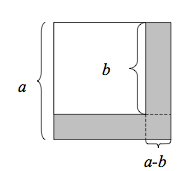
Kvadreringsreglerna är regler i algebran om hur man utvecklar uttrycken

[math]\displaystyle{ \ (a+b)^2=a^2+2ab+b^2 }[/math]	(Första kvadreringsregeln)
[math]\displaystyle{ \ (a-b)^2=a^2-2ab+b^2 }[/math]	(Andra kvadreringsregeln)

Texten i ovanstående avsnitt kommer från Wikipedia.se

Förklaring

(a-b)2 =  
(a-b)(a-b) =
a2-ab-ba+b2 =          ( och ab = ba )
a2-2ab+b2                V.S.B.

Länkar:

• matteboken om kvadreringsreglerna
• Kvadreringsregeln på Wikipedia.

Bondestam respektive Wille på Mattecentrum om kvadreringsregeln:

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

Potenslagarna, av Åke Dahllöfr

WolframAlpha Widget

Här kan du testa att låta datorn göra parentesmultiplikation:

{{#widget:WolframAlpha|id=c3f53c80c93fa003e2f8f54c64e0e386}}

Här kan du repetera konjugatregeln genom at expandera fönstret nedan:

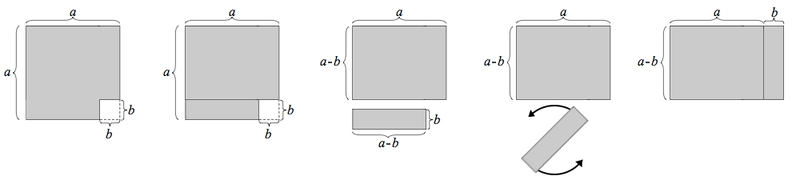
Konjugatregeln

Så här ser den ut:

a²-b² = (a-b)(a+b)

[math]\displaystyle{ (a-b)\cdot(a+b) }[/math]

[math]\displaystyle{ = a^2 +a\cdot b -a\cdot b -b^2 }[/math]

vi kan stryka ab - ba = ab - ab = 0:

[math]\displaystyle{ = a^2-b^2 }[/math]

V.S.B.

Film

Bondestam (tv) respektive Matteboken (th) förklarar:

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

Geometriskt bevis av konjugatregeln

Första beviset

Andra beviset

Visualisering

  Här gäller:

  [math]\displaystyle{ (x-y)\cdot(x+y) = x^2 - y^2  }[/math]

  Denna är gjord med Geogebra, sparad som animerad gif, upladdad till WIKIMEDIA COMMONS och länkad hit.

  [math]\displaystyle{ (a - b)\cdot(a + b) = a^2 - b^2  }[/math]

Länk till filen

Uppgifter

Övningar (utan räknare)

  1. [math]\displaystyle{ 1992\cdot 2008 = ? }[/math]

  2.  Lös  [math]\displaystyle{ x^2-1=0 }[/math] för alla reella x.

  Tips : Använd konjugatregeln och nollregeln för ekvationen.

Webbmatte

• Konjugatregeln på Webbmatte

Lektion 2 - Repetition potenser

Repetera avsnittet om potenser genom att expandera avsnittet nedan.

Ma3C: Sedan gör du uppgifterna i boken.

Här kan du repetera potensreglerna genom at expandera fönstret nedan:

Teori om potenser

GeoGebra

Aktivitet - Finn regeln

Fyll i luckorna i filmen

Uppgifter

Python

Resonemang om Gissa talet

Lär mer

[redigera]

En potens är ett uttryck som består av en bas och en exponent.

I sin enklaste form definierar vi potenser som resultatet av upprepad multiplikation.

Exempel
43 (utläses 4 upphöjt till 3) blir 4 · 4 · 4 = 64.

Potenser underlättar hanteringen (bland annat multiplikation och division) av stora tal. Primtalsfaktorisering är en stor del i det, men när vi väl har våra faktorer ser vi att de har en tendens att återkomma, då snyggar potenser upp vårt uttryck.

När basen är 10 och exponenten är ett heltal kallar vi potensen för en tiopotens. Med tiopotenser kan vi beskriva storleksordningen av reella tal.

Potenser kommer även senare att bli vår koppling till logaritmer.

Potenslagarna

Följande potenslagar gäller för potenser med reella exponenter.

Några förklaringar ("bevis")

Viktigt
Vi kan förklara negativa exponenter (tredje exponentieringsregeln), [math]\displaystyle{ a^{-n} = \frac{1}{a^n} }[/math] med ett exempel (inte ett formellt bevis) [math]\displaystyle{ \frac{1}{a^3}= \frac{a^2}{a^5} = a^{2-5} = a^{-3} }[/math] Man kan även visa nollregeln: [math]\displaystyle{ 1 = \frac{a^n}{a^n} = a^{n-n} =a^0 }[/math]

Grundpotensform

Definition
Grundpotensform Ett tal är skrivet på grundpotensform om: [math]\displaystyle{ a \cdot 10^n, där 1 \le a \lt 10 }[/math]

Grundpotensform är ett kompakt sätt att skriva tal som heltalsexponenter med 10 som bas. Formen används framför allt för att skriva tal som är mycket stora eller mycket små.

En regel är om man vill ta ut grundpotensen på 134 000 000, så förminskar vi talet så många gånger så att talet blir mellan 1 och 10. Du behöver nu multiplicera talet med ett tal som motsvarar hur många gånger mindre du gjorde talet, i det här fallet 100 000 000 = 10 upphöjt i 8. Svaret blir alltså 1,34 · 10⁸

• 10¹ = 10
• 10² = 100
• 10³ = 1 000
• 10⁶ = 1 000 000
• 10⁹ = 1 000 000 000
• 10²⁰ = 100 000 000 000 000 000 000

• 10⁻¹ = 1/10 = 0,1
• 10⁻³ = 1/1 000 = 0,001
• 10⁻⁹ = 1/1 000 000 000 = 0,000000001

Genom att använda grundpotensform kan ett stort tal som 156 234 000 000 000 000 000 000 000 000 lättare skrivas som 1,56234·10²⁹, och ett litet tal som 0,0000000000234 kan skrivas som 2,34·10⁻¹¹.

Ett tal skrivet i grundpotensform kan delas upp i två delar, först siffervärdet, därefter tiopotensen. För att talet ska vara skrivet i grundpotensform krävs att siffervärdet är ett tal som är större än eller lika med 1 och mindre än 10.

De flesta kalkylatorer (miniräknare) och vissa datorprogram utelämnar bas-siffran 10 och använder bokstaven E (som i Exponent) istället, till exempel 1,56234 E29. Detta E ska inte förväxlas med talet e. Det finns även datorprogram (till exempel programmeringsspråket QBasic) som använder bokstaven D istället då man anger tal på dubbelprecisionsformat.

Wikipedia skriver om Grundpotensform

[redigera]

Pröva på potensreglerna själv. Dra pricken "typ av uppgift" för att testa dig själv på olika regler. Välj visa svar när du vill kontrollera din egen lösning.

Sedan kommer en snarlik övning. Du kan välja att göra den ena eller den andra eller båda för att få problemen presenterade på lite olika sätt.

[redigera]

Kopiera texten till din dator och skriv rätt regel på strecket.

Förenkling	Skriv regeln
[math]\displaystyle{ {(x^3)}^4 = x^{12} }[/math]	_______________________
[math]\displaystyle{ x^0 = 1 }[/math]	_______________________
2 + 3 * 4 = 14	_______________________
[math]\displaystyle{ { \left( {x \over y }\right)^7} = {x^7 \over y^7} }[/math]	_______________________
[math]\displaystyle{ x^2 \cdot x^5 = x^{7} }[/math]	_______________________
[math]\displaystyle{ {(x \cdot y)}^{19} = x^{19} \cdot y^{19} }[/math]	_______________________
[math]\displaystyle{ {x^5 \over x^3} = x^{2} }[/math]	_______________________

[redigera]

På vissa ställen i reportaget har ljudet suddats bort.

Din uppgift är att beräkna vilka värden som saknas.

Du får googla så mycket du vill för att förstå hur du ska göra.

[redigera]

Kluring: Tala om vilket tal som är störst utan att använd miniräknare.

[math]\displaystyle{ 2^{36} }[/math] eller [math]\displaystyle{ 3^{24} }[/math]

[redigera]

Gissa talet

Gissa talet är en programmeringsuppgift som passar perfekt in på detta område.

Uppgift

Gissa ett tal Kör programmet tillsammans med en kompis. Kör det flera gånger. Turas om att vara den som kör programmet och den som gissar. Notera hur många gissningar som behövs varje gång ni kör programmet. Vilken strategi ger minst antal gissningar? Finns det ett maximalt antal gissningar om man följer strategin? Kan du uttrycka max antal gissningar matematiskt? Hur kan du uttrycka maximala antalet gissningar som en funktion av intervallet talet ligger i? Gå igenom programkoden och se om du förstår alla delar. Skriv ner de frågor du har om koden.

Python-koden

# förklarar syftet med spelet
print("Detta spel handlar om att din kamrat ska gissa det tal som du matar in. Skriv in kamratens gissningar och läs upp vad programmet säger. ")

# Ange ett tal
number = input("Ange ett hemligt tal mellan 1 - 100. ")

# använd heltal
number = int(number)

# räknare
guess = 0
count = 0

# räknare
while guess != number:

# gissa talet
    guess = input ("Skriv in talet (mellan 1-100) din kamrat gissar på: ")
    if guess == "exit":
        break
# räkna gissningar
    guess = int(guess)
    count += 1
       
# jämför gissning med tal
    if guess < number:
        print("Talet du angav ar mindre än mitt hemliga tal.")
    elif guess > number:
        print("Talet du angav är större än mitt hemliga tal.")
    else:
        print("Grattis! Du har gissat talet som jag tänkt på  (matat in).")
        print("Talet är:",number,)        
        print("Och det har tagit dig",count,"gissningar.")
        
# visar resultatet så länge vi vill 
input("Tryck Enter för att avsluta programmet")

Uppgiften är inspirerad av Attila Szabo, Utbildningsförvaltningen Stockholm.

[redigera]

[redigera]

Öva potenser

GeoGebra

Två övningar från Visuell matematik:

Tiopotenser och prefix

Exit ticket

- -

Lektion 3 - Polynom och faktorer

Här kan ni behöva gåt tillbaks till sid 52 för att repetera. Eller här: Ma1C - Potenser

Lektion 4 Faktorer rötter och nollställen

Ingången till denna lektion är ..

Diskreta och kontinuerliga funktioner

cvnG0YWPLjQ