Tryck: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) |
||
| Rad 134: | Rad 134: | ||
# Det här systemet fungerar som en hävarm och visar mekanikens gyllene regel. Det man vinner i kraft förlorar man i väg. | # Det här systemet fungerar som en hävarm och visar mekanikens gyllene regel. Det man vinner i kraft förlorar man i väg. | ||
# Detta är Pascals princip. | # Detta är Pascals princip. | ||
{{clear}} | |||
== Archimeds princip, s 112-114 == | == Archimeds princip, s 112-114 == | ||
Versionen från 2 april 2012 kl. 18.22
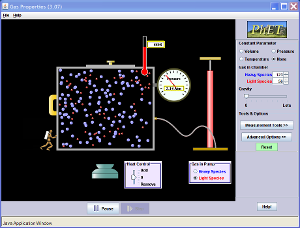
En simulering om gas i en behållare
.
.
.
Knappen har tyväär hamnat fel på något mysko sätt.
Vet ej varför.
..
..
Intro
Genomgång av provet
Intro: Filmen med tunnan. Plus mina elevers Colaburksfilm.
- Åkes infoblad om sinus och cosinus, mm.
- Stencilerna fr TEDT
Konvertera till SI-enheter
Som i all fysik är det nödvändigt att göra om de värden du får till SI-enheter innan du sätter in dem i formler och gör beräkningar. När du arbetar med tryck är det extra viktigt.
Antag att du behöver konvertera 24 dm3 till m3. Hur gör du då?
En enkel väg är att använda denna widget. Du behöver bara skriva in värdet som ska konverteras och den enhet du vill få det konverterat till,
Exempel: skriv 24 dm3 och m3 i respektive ruta.
{{#widget:WolframAlpha|id=6246bee639c7a7b11a08e34dd3cc6|theme=green|output=lightbox}}
Eller pröva att göra om 740 mmHg till bar.
Tryck mellan fasta kroppar, sid 105-106
p = F / A där p är trycket i N/m2 = pascal, Pa F är kraften, ofta mg. Kraften anges i Newton, N. A är arean i m2
Omvandling av tryckenheter
Tabellen kommer från Wikipedia.
| Enhet | Motsvarighet i kPa | Motsvarighet i bar | Motsvarighet i PSI | Motsvarighet i mmHg | Motsvarighet i mmVp | Motsvarighet i mVp | Motsvarighet i atm |
|---|---|---|---|---|---|---|---|
| bar | 100 | 1 | 14,5 | 750,06 | 10190 | 10,19 | 0,99 |
| PSI | 6,89 | 0,069 | 1 | 51,71 | 703 | 0,70 | 0,068 |
| mmHg | 0,13 | 0,0013 | 0,019 | 1 | 13,59 | 0,01359 | 0,0013 |
| mmVp | 0,0098 | 98·10−6 | 0,0014 | 0,074 | 1 | 0,001 | 97·10−6 |
| mVp | 9,81 | 0,098 | 1,42 | 73,56 | 1000 | 1 | 0,097 |
| atm | 101,325 | 1,01325 | 14,70 | 760 | 10 330 | 10,33 | 1 |
Räkna 601-607
Tryck i vätskor och gaser, s 107-111

to v 8
En tillbakablick
GGB med mätvärden och derivator
Tryck i vätskor
p = ρ g h (Pascals lag)
Sir Richard Branson
Kolla filmerna och besvara frågorna:
Hur djupt kan undervattensfarkosten gå? Vilket är trycket där? Gör ett antagande för glasets yta och räkna ut vilken kraft det måste tåla
Hydrostatiska paradoxen
Trycket på botten av ett kärl beror bara på djupet inte på formen. Med djupet menas avståndet upp till vattenytan.
Pascals princip
Trycket i någon del av vätskan överförs till alla delar av vätskan.
(P1) = (P2) (F1)/(A1) = (F2)/(A2)

Den övre/vänstra filmen innehåller ett fel, vilket? Den högtra är bra men använcder ovanliga enheter. Var används dessa?
Evighetsmaskiner finns inte eller hur...
Lösningar: Lösningar till uppgifterna 608-613
Diskussionsuppgift

Figuren visar ett bromssystem men en pistong (1) vid bromspedalen och en pistong (2) vid bromsskivan. Pistong 1 är grövre än tvåan. Vilka av följande påstående stämmer?
- p1 = P2
- A1 = A2
- F p1 = F2
- Det här systemet fungerar som en hävarm och visar mekanikens gyllene regel. Det man vinner i kraft förlorar man i väg.
- Detta är Pascals princip.
Archimeds princip, s 112-114

Arkimedes princip beskriver den kraft som påverkar ett föremål vilket sänks ned i en vätska. Den säger att "ett föremål nedsänkt i vätska påverkas av en uppåtriktad kraft, som är lika stor som tyngden av den undanträngda vätskan". Lyftkraftens storlek F är alltså proportionell mot volymen V av den del av föremålet som är nedsänkt i vätskan genom sambandet F = ρ V g, där ρ är vätskans densitet och ρV därmed den undanträngda massan medan g är jordens tyngdacceleration. Principen upptäcktes av Arkimedes.
Om föremålet har lägre densitet än vätskan, blir lyftkraften så stor att föremålet flyter. Har det större densitet än vätskan, till exempel järn i vatten, kan det fås att flyta om formen anpassas så att föremålet exempelvis förvarar luft under omgärdande vätskeyta. I detta fall blir densiteten av "föremålet", som tränger undan vätskan, ett medelvärde av järnets och luftens; medeldensiteten för föremålet blir lägre än vätskans densitet.
Observera dock att Arkimedes princip gäller även i andra media än vätskor. Sålunda påverkas varje föremål som befinner sig i luft av en lyftkraft, om än liten. Också här gäller regeln att ju större föremålets volym är, desto större är lyftkraften. Därför har i en normal situation en klump bly en (marginellt) större tyngd än en mängd bomull med samma massa. Texten ovan från Wikipedia
Demo: Fingret i vattenglaset:
Lösingar: Lösningar till uppgift 614-620
Lufttryck, s114-117
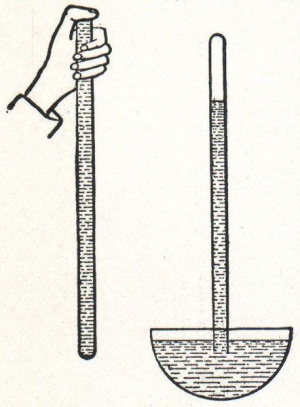
På 1600-talet försökte man pumpa vatten ur gruvor. Man märkte att man bara kunde pumpa 10 m högt.
Normalt tryck vid havsytan
p0 = 101.3 kPa
Totala trycket i en vätska
p = p0 + ρ g h där p0 är lufttrycket mot vätskeytan ρ är vätskans densitet g är tyngdaccelerationen h är djupet i vätskan
Lösningar: Lösningar till uppgift 621-625
Ideala gaslagen, s 118-120
to v11
Allmänna gaslagen
pV = nRT där p = trycket, V är volymen, T = temperaturen, n är antalet partiklar i gasen och R är allmänna gaslagen. R = 8.314 J/(mol*Kelvin)
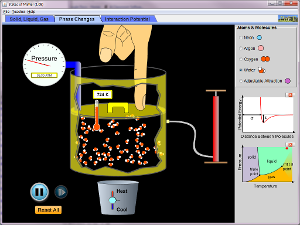
Simuleringar
Här är två olika simuleringar av gaser i behållare:
En klurig film
Nu är vi klara med detta kapitel och har alla verktygen för att förklara vardagliga fenomen exempelvis det i filmen nedan:
Laboration på gång
Dela ut labbinstruktion till Arkimedeslabb.
Länkar: Ideala gaslagen
http://sv.wikipedia.org/wiki/Ideala_gaslagen
http://sv.wikipedia.org/wiki/Boyles_lag
Diagnostiskt test
måndag v11
Diagnostestet tar cirka 40 min. Här finns facit till tryckdiagnosen.
Därefter finns tid för att räkna uppgifter ur boken.
Laboration - Arkimedes
Torsdag v11
Före vi labbar går vi igenom diagnosen helt kort, cirka 10 min.
Vi labbar i helklass. läs på instruktionen i förväg.
Repetition
Låt oss först konstatera att det här är ett relativt lätt prov. Det rör sig om ett kapitel. Och ett ganska kort ett dessutom. Femton sidor och tre formeler....
Pluggtips
- Börja med att läsa sammanfattningen på sidan 121 så att du får en känsla för vad du behöver lära dig mer om.
- Du bör läsa sidorna 105-120.
- Titta gärna igenom denna sida på wikiskola.se
- Exemplen: 6.1-6.8 är alla lämpliga att studera noggrant. Här ser du exakt hur du kan ställa upp dina lösningar.
- Räkna många av de blandade uppgifterna på sidorna 122-123.
Läsanvisningar
- Sid 105 är ger dig formeln för tryck mellan fasta kroppar och dessutom omvandling mellan enheter.
- Vätsktryck på sid 107 är viktigt.
- Läs om den hydrostatiska paradoxen och Pascals princip så att du har det med dig för kommande resonemang.
- På sidan 112 bör du läsa noga om Archimedes princip även om du inte behöver kunna göra härledningen själv.
- Du läser om lufttryck på sid 114-115 för att förstå hur formeln ska användas.
- Läs texterna på sid 116-117 som allmänbildning i fysik.
- Allmänna gaslagen på sid 118 är betydelsefull, speciellt som den tillämpas i Exempel 6.7.
- Läs sidan 127 för att det är kul att veta mer om dinosaurierna.
Övningsprov
Öva på ett gammalt prov från Örebro, Med lösningar.
Vi delar ut ett övningsprov med G-uppgifter om Tryck.
Facit till Prov: Tryck version 1 med lösningar
Förnöjande film