Geometri 2C: Skillnad mellan sidversioner

Från Wikiskola
Hoppa till navigering Hoppa till sök
VisuellWikitext
Rad 121: Rad 121:
[[Fil:Likformighet2.png|thumb|372px|right|]]
[[Fil:Likformighet2.png|thumb|372px|right|]]
[[Fil:Likformighet4.png|thumb|185px|right|Svaret]]
[[Fil:Likformighet4.png|thumb|185px|right|Svaret]]
----


'''Användningsområden'''
'''Användningsområden'''

Versionen från 13 mars 2012 kl. 21.17

<facelikebutton style="2" showsend="0"></facelikebutton>

Animated construction of Sierpinski Triangle
Animated construction of Sierpinski Triangle

En datauppgift

Inloggning på wikiskola

Ett användarnamn som är ditt exakta förnamn plus Initialen i ditt efternamn

Kunskapskrav

Betyget E

Eleven kan översiktligt beskriva innebörden av centrala begrepp med hjälp av några representationer samt översiktligt beskriva sambanden mellan begreppen. Dessutom växlar eleven med viss säkerhet mellan olika representationer.

Eleven kan föra enkla matematiska resonemang och värdera med enkla omdömen egna och andras resonemang ... ... Dessutom uttrycker sig eleven med viss säkerhet i tal, skrift och handling med inslag av matematiska symboler och andra representationer.

Genom att ge exempel relaterar eleven något i kursens innehåll till dess betydelse inom andra ämnen, yrkesliv, samhällsliv och matematikens kulturhistoria. Dessutom kan eleven föra enkla resonemang om exemplens relevans.

Eleverna bygger sidorna

Utifrån grundformen med en film en länk till Khan osv får eleverna uppgiften att bygga en sida var under kursen. ett avsnitt var alltså. Och detta gör de i början av kursen för att få ett hum om vad kursen handlar om. Det är sexton avsnitt i kap ett och det är 16 elever.

Jag har markerat i min matematikbok vilka teoribitar som kan komma ifråga.

Minst:

  • En film av Matteboken, Bondestam etc
  • En Khanlänk
  • En text
  • En definition
  • Ett exempel
  • En uppgift
  • En bild. Helst från Wikimedia Commons
  • En länk till fler förklaringar
  • En länk som knyter ant till matematikens kulturhistoria
  • Ett försök att förklara vad man ska ha detta till

Editering

Editera under er egen rubrik. Inget kan gå fel. Allt går att rädda.

Titta på färdiga sidor hur man kan göra och härma wikikoden.

Läs mer om Wikimarkup och hur man editerar.

Milstolpe

Ditt arbete ska vara färdigt för bedömning måndagen den 12 mars.

Vinklar

Läs Ma2C s. 66-70

Genomgång

Vinkelsumman och yttervinkeln finns visade på Geogebra.se

Definition: Vinkelsumma 

Vinkelsumman i en triangel är 180o

Definition: Sidovinklar

Sidovinklarna är tillsammans 180o.


Definition: Vertikalvinklar

De två vinklarna är vertikalvinklar.

Definition: Alternatvinklar

De två vinklarna är alternatvinklar.

GeoGebra om Alternatvinklar mm.

Sats: Yttervinkelsatsen

Yttervinkel till triangeln.
Yttervnkeln är lika stor som summan av de två motstående inre vinklarna.
Gamma = Alfa + Beta

Bevis: Yttervinkelsatsen

Länkar

Malin Christersson har en fin sajt där jag hittade en Geogebra om yttervinklar: http://www.malinc.se/math/basicgeometry/exterioranglesv.php

Likformighet och kongruens

s. 71 -74


AmmarA - Likformighet

Alla figurer av samma färg är likformiga.

Definition

Likfromighet är två objekter som har exakt samma form, men är inte lika stora (se bild på höger).


Två trianglar är likformiga om något av följande är uppfyllt: 

VVV: Motsvarande vinklar är lika.
SSS: Förhållandet mellan de tre sidparen är lika
SVS: Förhållandet mellan två sidpar är lika och mellanliggande vinkel är samma

Video

Load video
YouTube

Exempel (Uppgift) ⇒⇒

Exempel
Formeln
Svaret



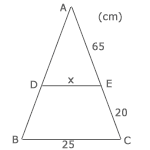
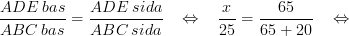
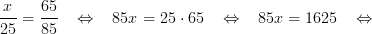
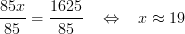
Användningsområden

Man kan tex. använda likformighet i avbildningar när man ska rita kartor och jorden på olika skalor, dvs. 1:2, exempelvis:-

Den här figuren är en avbildning av figuren till vänster i skalan 1:2



Länkar

TildaD - Kongruens

Defination: Två figurer är kongruenta om de har samma form och samma storlek.

Två trianglar är kongruenta om något av följande tre fall gäller:

  1. Två sidor och mellanliggande vinkel (SVS = Sida-Vinkel-Sida)
  2. De tre sidorna (SSS = Sida-Sida-Sida)
  3. Två vinklar och mellanliggande sida (VSV = Vinkel-Sida-Vinkel)

Länkar

Bilder


Load video
YouTube

Längd, area och volymskala

Förra veckodiagnosen ?

s. 75- 79

Tisdag v 8.

Håkans tips

  • klippa in en svg-bild fr Wikipedias source

Definition 

 Skala =  En sträcka i bilden / Motsvarande sträcka i verkligheten


Definition: Längdskala 

 Längdskala = Bildens längd / Motsvarande längd i verkligheten


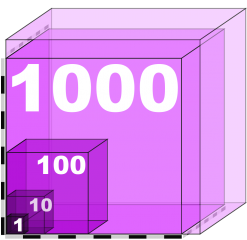
Definition: Areaskala 

 Areaskala = Stor kvadratens area / Lilla kvadratens area



Definition: Volymskala 

 Volymskala = Stora kubens volym / Lilla kubens volym


Länkar

ViktorE Skala

Topptriangel- och transversalsatsen

Tisdag v 8.

Håkans tips

  • klippa in en bild från wikimedia commons

Geogebra för att bevisa

NilsG Topptriangelsatsen

81- 85

[MalinC Brättar om topptriangelsatsen]

Load video
YouTube

Transversalsatsen


<ggb_applet width="796" height="336" version="4.0" ggbBase64="UEsDBBQACAgIAPu7VUAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAD7u1VAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1a2ZLbNhZ9dr4CpYd5mUjCDsKjdspbKq5ylqr2TE3NyxQlQhLTFKmQVC+p/E6+ZH5sDgBSq+3u9pK002U1SOIS9+Kcu0HtyTfXq4JcurrJq/JswEZ0QFw5q7K8XJwNNu18mAy+efLVZOGqhZvWKZlX9SptzwbSS+bZ2cCYuRaap0Mt0/lQ8mw+tEa54XzK05nTZiaT+YCQ6yZ/XFY/pCvXrPH8fLZ0q/R1NUvboHjZtuvH4/HV1dWoVzWq6sV4sZiOrptsQGBm2ZwNuovHWO7gpSsRxDmlbPzv71/H5Yd52bRpOXMD4rewyZ989WhylZdZdUWu8qxdng0SKgdk6fLF0u/JsAEZe6E1AFm7WZtfugav7t2GPber9SCIpaWffxSvSLHdzoBk+WWeufpsQEfCWq6EEUxIwROhzIBUde7KthPulY775SaXubuK6/qroBJmtlVVTFO/JPntN8Ipp+RrP7A4cAxaxykan1ERBx4HGQcVZWR8XUZRGWVklJFiQC7zJp8W7mwwT4sGEOblvAZ92/umvSlcsKd7sNs++xp7avJfIcwo/CRiHm6+9h+Nj/QT48NNsj2tbb25p9JepTT3UMk/RqXoVQrOTlVy9Y5d6veAG224yzaZ2tsmVIV/4XOiUfB7aIz3tykUiVdoEvlWhVr+IVucjPtImXTBQZqll+2YbN2q8eEiLFHWez0jCqGhDZxcEWYxGE4QDIQpIhVuWUK0Hw0RBhOSCJIQL8cECbGhEvySJiymicJi/qlBSBIGRZIoQVgIKUkQSCSEJUKUC0goRRRe8uoZ90sITaTGnUiIhI0+Ig2DoMCLuId6TgQjwr/MDOGaaL8ekz7SdeJNx5KcaEo08wsiqBHQMZghnxDhd6M7uPJyvWkPIJqtsv6yrdZbLiCNdLTLejE9HSTFR5MinboCdeLcM0nIZVr4iAiK5lXZkp5EHp8t6nS9zGfNuWtbvNWQn9PL9HXauutvId30uoPsrCqbn+qqfV4Vm1XZEDKrCrq1uSrY3jXfWo0bsTch9yfU3oTeuzZv1VthhmwaB/1V3fTiaZa98hK71AAkfyyLm2e1Sy/WVX64jck4lJyJ28yKPMvT8l9wVq/F40L6ChSyVV+BBEt6Q6o6O79p4MHk+j+urjBHR1xQavAjFVWJRR25iVM80SONUiYox+/EUJ+YZqkPPm5HzEjGE8OUMlxohbf6uZFNLE14YoVMEsl11O0utxSl126320XtQ3vv5lXzrCp2jwIAz9N1u6lD9wAjar+tp+WicMFJQmijNM8uptX1efQOEdd6c7PGHY0WTBcBeILkwH2BXnTjFKNSUcabtpWiQYYGCdq7W55t55nlQSKM0zgGKfhvNK3bKuu3yWivJm9CSqODLnD6dOW931f6TZm3r/ubNp9d7LbqX/hhs5q6rQ8drsk+1ZqT8ZGTTS5cXbqi82mQuak2TQzRPXfP3Cxf4TZOdJCknq5/woD4NHOL2vWGF6Ezi4CFWbrvriePw1Lf1tXqVXn5Br5wZMBk3Fs5aWZ1vvY+R6aoAxdu51VZ3qQoI9n+ez4IsfWZLxeAp/XQIDw37bIC2d/97/eLtCQvC/RfTZsvsAayDCR8LBZuhc6LtMHdgsduYX8aejqPL6mmPyPRbWthnN8RiOm3up53TpIW62Xq+74OhCK9cfUBLGG976vsGCxwEXaEqF/7BTzba+eio0SLcbHGgiG+DvIW8G/Ite/LJaOIaqUNek7p/f0GtXNEubUW7R0VqJ7IMuTX2O3Hdtfj4OPxIInHp0ekwtMihLeA+exhgfkhUDJo5UmSsIRzrQW3MmDJ1EgIyRSaecV9U//ZsXz+5WNpRowrzaWyOkErzk2A0tiREYoZPFJGWP1JkJxVq1VaZqQMzeZPVXGzqMrBrv1JqQ91kjLvpCTlHt8I3qbt57u3WBSbRbEUA/qLaVTYqXkLdVFhT852qcNy06IVusBxrwlHkLarfuHiuzzLXGiDx+/nfQ/pfeKZEoF6xbp6uGOe3Yf5d7tn4xb+bmvI7BYHvb+h93TRnaMNEbUCh1ot0NEgdgUXXQbUzFgLL1T4JJRHX4NfWk6ttgZNEDVMHrcFd+fJ/VLGV5pYq/PVushnebt1rsLHx6uyRVVyoXSdFuQL59a+E/qxfFOnZeO/bIkye4X+jpykD4gTjapEGeUS7alCwxmjf4j+kyKJGu4JEcixJpCiLShMLPIFY8Jaw/4ynEwfDidGjgxVDBGiFcBWtqcEMWCERLsgQIvwdQOUDAWqXqJ9NGlqkcZP2ucHzMlxQfCl9bAcTE8KwIvbkvx+fX7xQfUZaSieSfz4MJpHNZIWZ0VBhTbwAqODUwg5SpBNheKGWTRCn6FKv4YfHXHyoq+9x9Rk76fGu+QW+ezDAu7wOPmHV6Uh0t6IMVQmg9woeMLF5wm3dxOyDb8jVrLISnrCysv7BMzLDwoYHb8J0PGLAD98PDFC+kQIj/d+ryzgjj2+pobD6yXiAC2+pdHphWUQRvtqZSJ0wrX6hDFw3hWLQ8CfR8BfnAA+fz/gx6Vn/tFniE8SCBK5xGohBX6METEKhmykUWAoU5oyBlRZV3VYYkdAWXL/tRf6BjQIX2rZeTu7XZJ7esKuux+77mGwy0EXRYZDdDDNNE9kzy9NkPK41L7ZThLZ0cv1iAqJ6FKCQ1x9pjT3p9H7LNL78oTexf3oXTwMeocc9Qo5MvEHeJQsybf8MpVIpa3UXCQ+pwaCuUFDgYOV5Examyj5Vwvfl5Hf0+8Plvfjd/lA+BUJDgXCSIlQ5GovfPEokG6VlpbZWA0lkyPLqK+PGsc7pvUXRK+7XtcwzHfMHcgXl1X7X7TImMGyZEy6v4MdUlduVq7OZ4Ojt7x+6Np00LKRopqh39PWotbpxNydPnZHU3ln6hKmLu5sKr/V1E9q6Rt33faY/u2XTdX+Yz52Z/GK/J30mJ8a3+LFweEqf2Yr37Rp3YajIwlt40gwg4TnQ0LiPGxViBSdID8qSgXFIdoqcXBUuh0ofgDUcrw4AorfCSj+kIDCuYehczNGaZR4RXk8UmoDoOBzOPpIiVNl8i6gxvt/6gl/Uu3+d9CT/wNQSwcI4u9Zvw0JAAC6JAAAUEsBAhQAFAAICAgA+7tVQEXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICAD7u1VA4u9Zvw0JAAC6JAAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAKUJAAAAAA==" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

Randvinklar och medelpunktsvinklar

86-91

Onsdag v 8.

Vi har en kort lektion för tre tunga geometriska satser. Så ser grovplaneringen ut och vi måste komma vidare till avsnittet om räta linjen. Det säger sig självt att vi kommer att behandla detta översiktligt (inte så noga alltså). men vi kommer att repetera detta när ni har lagt in ert material. Ni kommer inte undan er uppgift att skriva på wikiskola för det där med att kommunicera matematik är ett viktigt grundmaål.

Även om dessa satser är intressanta är det inte centrala. titta på beskrivningen av det cerntrala innehållet i geometrin: 

  Användning av grundläggande klassiska satser i geometri om likformighet, kongruens och vinklar.

Med klassiska satser om vinklar menas förmodligen vinkelsumman och yttervinkelsatsen tillsammans med begreppen sidovinklar, vertikalvinklar och alternatvinklar (och transversalen). Jag ska titta i en annan bok hur de tolkar kursplanen.

Nåväl, något måste vi göra och min idé är att vi tar GeoGebra och konstruerar alla tre geometriska figurer och sätter oss in i vad de betyder på detta sätt. På det viset kommer vi att prata om och jobba med begreppen och det ökar chansen att vi blir bekanta med varandra.

Håkans tips

  • bädda in youtube. Det kan vi göra med Nils film ovan.

Extramatten

Extramatten idag handlar om att repetera inför omprovet

DenisJ - Randvinkelsatsen

Håkans GeoGebra om randvinkelsatsen

<ggb_applet width="554" height="521" version="4.0" ggbBase64="UEsDBBQACAgIADa5VUAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIADa5VUAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vrbcts4En3OfAWKzxGFO8CUnCnFuWxqM5OpcXZra98oEpI4pkgtSdlyan5q5/Ib803TAEhdLPmixEmUuBJTJJpodJ8+3Q3Ig++XsxxdmKrOyuIkICEOkCmSMs2KyUmwaMY9HXz/9LvBxJQTM6piNC6rWdycBNxKZulJME5HIxpT1Rtxk/S4lqoXjcakp7WUOkqNZglIomWdPSnKH+OZqedxYs6SqZnFb8okbpziadPMn/T7l5eXYacqLKtJfzIZhcs6DRAss6hPgvbDE5hu66VL5sQpxqT/nx/e+Ol7WVE3cZGYAFkTFtnT7x4NLrMiLS/RZZY205NASBqgqckmU7BJKhKgvhWag0PmJmmyC1PDqxu3zuZmNg+cWFzY8Uf+E8pX5gQozS6y1FQnAQ65IJFQNBJMMSkFVwEqq8wUTSvcKe130w0uMnPp57WfnEoeoKYs81Fsp0S//ooophg9thfiLxQuUvoh7J9h5i/UX7i/CC/D/evci3Ivw70MZwG6yOpslBtAOM5rcGFWjCuAb3VfN1e5cetpH6zNJ4/Bpjp7D8KgL0De57Dwx/gxx+6/t3nDQLKhsakWByrs1AnB76eOfpSB7Ebz6E3myVsUenvvYx8RG/oEfuz+uf87GtltJl7X6O/vUsi0Vag036tQ8s9i4qDf0WPQMgLVUyvbRk1jZrXlCIuQiGyoEySAD1JBZAtEIrgoioABiAjEBdwSjaS9KsQUDHDEkEZWjjDkCCE0/OLKTSaRgMnsUwU8RAQUcSQYIo5HHAF7kOMi8JIykBACCXjJqifUTsEk4hLumEYc1mhpqAgIMngR7kE9RYwgZl8mClGJpJ2PcEtvqe3SYUqKJEaS2AmBycBiz2CQ14hZa2TrrqyYL5otFyWztPvYlPMVFiANOWid6nxO2sqEjwZ5PDI5FIcziyRCF3Fu2eAUjcuiQR2I2j+bVPF8miX1mWkaeKtGv8QX8Zu4McuXIF13up1sUhb1T1XZnJb5YlbUCCVljldrLnOy8ZmuVg03bGOAbw6IjQG58Vnt1VvCCFrUBvSXVd2Jx2n62kqs0wJ48m2RXz2rTHw+L7NtMwZ9V2cGZpHkWZrFxb8hWK0W6xe0Kjs2TXVlh0esW0hZpWdXNUQwWv7XVCX4kYSMac1ppATFUgToyg8wpkIGWVtTHnEmuYKqUiexpR6HdyhlhGMeCajHEAhXNwwpr9hcrPCJl2Zt6qRyFX5987p+VubrR87603jeLCrXL0BarKxNw2KSGxchjtdQjJPzUbk886HB/FzvruZwh/0KRhPndQSZgQqwctJeR/7qZOzSVlLYyWAngbtYy9LVOImok3DXkb86KQhev7TWVNKZSXCnJqtdPsNBy5ouV9nQt7V9UWTNm+6myZLztan2hR8Xs5FZBdD2nOSh5hz0r0XY4NxUhcnbgAYwF+Wi9vzciPXUJNkMbv1AZ7GF61+wAP80NZPKdAvPXS/mHbb5jo/VncduqpdVOXtdXLyDWLi2gEG/W+WgTqpsbmMOjaAInJt1VKVZHUMNSTffswwE0xNbK8A9jXUNcHPRTEsA+8zMsiKussUM/RNyS1rBe/V5mccFzAYPQNZSMjcz6LpQ4wLPxe4KgKHr56ynUTn6BfLdqiT68TWUMLw3CF24xvl8Gtuer3VHHl+ZastBbr4fyvS62wAVZxuQf24nsLjPjfEh07RUQXOY0DFtK30BEjVaQgEOCQT7FawltMX/ve/nfUNrrbX828rY/uk1ECGyvKPucNmzXZdtB/XGGo/YaTSUzmcipPJBfJaUs1lcpKhwfc9pViW5CdaFOMY22lBMrAe9cxZNN5D4ydopdgAAFmTJyr/JHTF7D//jD/f+Oo82UODPYedSu6565Xb74R9ZmhrX3Pk6k01McQErhfoKW0LcbjivsNeP3ndPluCdnnt0RdpH78kGNIB7lS3RsJMfdlJDaAwoCTWmGm5YO+8QuoKeZ8cQeoKe44df0f8Kb0Tt063tdbJxltwO6k+OCNuYJjtgnt4O5jabTj8oARHqa6W7HgefGLiZM0wYrIXJCNtOx9FLRVRRrIRkmkXqE1Dtfqg8PwSV598KKjxUmEUR1ZoqzHVbJ4AI0EJSIrjilGusbIP54LicmYl9fg2ZU58Dn+8AFN8OUN3O1kEQf9EsuPawCjWDTl5ShiWjmPuqQkKhIhkRIRSRKsJ2jwwO7jEWShpxwhSlShCtPiKpXkth2WyeZ0nWrByb27h4XTTQPxrXQO22hefGzG0//rZ4V8VFbQ/5vMxGu/lRrHtxCOtefCus0yGRWOGIYQwbOCW1Zx0JlVZUYAapMMKci0/ReNzKuhc7AI0OY93oaFgH/IoUIRRTxTkRbbEB33KsIsWVxFoyTzpBQy2kJFozIkmkd3aEXw3p9oP7woM73AE3PQzc9EjA7fGQ4C2irKvWJq2U5w+NQq2wJkpjpjBmXH9j+A5vKpnmMHzNkeDLQyiXm91Hlx45pE0MpLZfmgBb/V62RxkMEPtGBGRnLPpq4XXnY9fAfe7BtQma7kvQf/3/dpDdycsKQpC278N6Fp33Q6aVAMdBqoQ2RHenah925kHwbhyQW+Pg7Xhcm8bCbg8ALc58b5SQD0c1rpKNqtlV8jwvL38249wsndsfAKPhjRj9dhBGv+1ipAAi2DJRjgmkNvKlIKK+UzluhO7Xeb48pPN8edeZ1lfTeqqQatiLQGaFQIL6SbrSSWAvQgXUTiLh96fY79kjr8UscQdfwyrZz6GXN3FofI8jsHlcrTEbf1g1675m8CQR5IFPwqLjOQmDBrn7ueNMDG/8cHYUpfJ+JH91CMlffSvbSwJ6NRFMUCkotMH+UIeHkmEd2RMHaJc40Z9tc/nqpv50clh/OjmS/lSGUjFCCIYduoh45E8yeyJkUKY5ZZqCjyPsHdzjwCBFmVSEERZxJr7a9vTW3eWrHXSnh6E7PRJ0IfkBOQi3VRCqoZZMtEd2EcUAbSR5pIBH1NdIISCXRpK6xkwK/E3uPl7d2Nn+flBn+/vduw/5pXrbyH9Fuj9KjqW33YfRiy2MdrPsX38chNEf1zGCAI+EtJEvCOQ9vG/3cZ9u+OYveO+9/Wh3iOyrBWl4I0h/HgTSn7sgCXvEFbkzTCnJXh59HpR6MmphYkcGU3/zz0Xc32S1f1P89G9QSwcImk/H6UcJAADwLAAAUEsBAhQAFAAICAgANrlVQNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICAA2uVVAmk/H6UcJAADwLAAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAN4JAAAAAA==" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

FredrikJ-Bisektrissatsen

Länkar 

Text om Bisektrissatsen.....

Defenition...

Bisektrissatsen = AD / BD = AC / BC

AntonL - Kordasatsen

Koordinatgeometri

s. 92- 101

Torsdag v 8.

RikardM - Avståndsformeln

Load video
YouTube

WilliamM - Mittpunktsformeln

"P1" är punkten 1, "P2" är punkten 2, och "M" visar var exakt var mitten av punkterna P1 och P2 är. Bilden är tagen från Wikipedia.
Mittpunktsformeln är en mattematisk ekvation.
Två punkter P1 och P2 som kan ligga precis var som helst i 
ett  kordinatsystem, med hjälp av mittpunktsformeln bestämma 
punkten mitt emellan Punkt1 och Punkt2 som har benämningen M.


Definition 1: 

(X1,Y1) och (X2,Y2)
(Xm,Ym)= (X1+X2/2),(Y1+Y2/2)
Förklaras i videon

Definition 2: 

Det gick inte att placera definitionen från Wikipedia, eftersom den inte stöds,
gå in på länken och se efter själv:Wikipedia, Mittpunktsformeln
O = Origo.
M = Punkten mellan P1 och P2.
P1 = Punkt1.
P2 = Punkt2.

Exepel på problem 

Du har två punkter (1, -2) och (-3, 5), hitta mittpunkten av de två punkterna med hjälp
av mittpunktsformeln.

Lösning 

y 1 = -2, x 2 = -3 och y 2 = 5.



LÄNKAR 

Exempeluppgift
Svårare Exempeluppgift
Film om Mittpunktsformeln
Khan Acadamy

FelixN - y=kx+m

       K = lutningen. Man kan räkna ut K om man har två koordinater t ex x1-x2/y1-y2 = K
       M = Var linjen skär y-axeln
       Exempel uträkning med koordinater.
       (-1,1) (1,5)
       y= valfri Y-koordinat, vi väljer 5. Formeln blir då 5=kx+m
       vi räknar ut k
       k=(x1-x2)/(y1-y2)= 5-1/1-(-1) = 4/2 = 2, k=2. Formeln blir då 5 = 2x+m
       x = 1. Formeln blir: 5 = 2*1+m. Tar bort 2 på båda sidor. 
       M= 3

Fil:Http://upload.wikimedia.org/wikipedia/commons/0/0e/FuncionLineal04.svg Länkar:

http://www.youtube.com/watch?v=obtLcSrvE_Y 

http://sv.wikipedia.org/wiki/Linj%C3%A4r_ekvation

Riktningskoefficienten

s. 102 - 104

Håkan länkar

SamN - riktningskoefficienten

Slope picture

Bestäm riktningskoefficienten för den linje som går genom punkterna (1.2) och (4.-3)

Uträkning för riktningskoefficienten

-3-2/4-1= -5/3=-5/3

http://www.matteguiden.se/wp-content/uploads/2010/01/linjes-lutning-4.png

http://www.matteguiden.se/wp-content/uploads/2010/01/linjes-lutning-3.png


Definition

Y=kx+m


Ett Exempel + uträkning till exemplet

Fråga 1

Erika anställer en städslav och får betala för 4 timmar 450 kr och för 9 timmar 990 kr Erika betalar både grundavgift och en avgift per timme. Hur stor är avgiften Erika måste betala?

Uträkning till fråga 1

Tänk så här:

Kostnaden ökar med 990kr-450kr= 540kr

Tiden ökar med 9-4= 5timmar 990-450/9-5=540/2= 225

Avgiften per timme blir = 225 kr

Länk

[riktningskoefficienten ]

lov

Räta linjens ekvation

Onsdag morgon

s. 105-109

För att rita en rät linje eller för att skriva dess ekvation behöver du antingen:

  1. två punkter på linjen eller
  2. en punkt på linjen och dess lutning

En punkt på linjen kan vara att veta var den skär en axel, exempelvis y-axeln.

Parallella och vinkelräta linjer

Onsdag 10.30-12

s. 110- 112

Två linjer är parallella om de har samma riktningskoefficient.

Parallella linjer 

k1 = k2

Två linjer är vinkelräta om produkten av riktningskoefficienterna är minus ett.

Vinkelräta linjer 

k1 * k2 = -1


<ggb_applet width="498" height="595" version="4.0" ggbBase64="UEsDBBQACAgIANy8ZUAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICADcvGVAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbNVYW2/cNhZ+Tn8FoYd92M1oeBeVHadogi0awL0ATouiLwtK4ozV0UiqRI1niv6d/pL9Y3tISnOz48Tb2yawTZE8PIfnO1dm8eluU6Gt6fqyqa8iEuMImTpvirJeXUWDXc5U9OnLTxYr06xM1mm0bLqNtlcRd5RlcRUly6USQi9nGZXpjBcpn2WFpDOaZKmiJktxkkcI7fryRd18pTemb3VubvJbs9HXTa6tF3xrbftiPr+7u4snUXHTrearVRbv+iJCcM26v4rGjxfA7uzQHfPkFGMy//7L68B+Vta91XVuIuRUGMqXnzxb3JV10dyhu7Kwt1eRwDJCt6Zc3YJOCVMRmjuiFgBpTW7Lrenh6MnU62w3beTJdO32n4UvVB3UiVBRbsvCdFcRjkmaSKq4UDxVmLIkQk1XmtqOtGSUOZ+4LbaluQts3ZeXyCNkm6bKtOOIfvkFUUwxeu4GEgYKg5RhC4c1zMJAw8DDIAIND8d5IOWBhgcaziK0Lfsyq8xVtNRVDwiW9bID6x3mvd1Xxt9nXDhqT56DTn35MxATDG4SIPeT5+5Xwi93G/NzJcmJVNsNTxQ6iQSUP1wk/U2KskfVpOIdaspHhAa9P0RPIk5kgij/43/vSWSPqXkpMczfJ5ApJzBR/EGBkv8pKi7mU6gsxuhA/a2jHb3Hmk3v4oWlSKTO7QkSEBsyAS8XiKQwJBRBNCAiEBcwJQpJNyaIJbDBEUMKOTrCkA8OoeAPTzwziQQwc6sJxCQiIIgjwRDxMcURRBLycQkxShlQCIEEHHLiCXUsmERcwowpxOGOLiQTAoQMDsIcxFPECGLuMEkQlUg6foS7UJfKXR1YUiQxksQxhKiGiA7RDPQKMaeNHOEq63awZxDlm2L6tE17sAVQQz46Zr2Qn86S4rNFpTNTQZ24cZZEaKsrFxFe0LKpLZqMKMPaqtPtbZn3N8ZaONWjH/VWX2trdp8DdT/J9rR5U/ffdI193VTDpu4RypsKH+7cVOTkmx5uDRN2ssFPN8TJhjz5Th6U28AOGnoD8puun8h1UbxxFMfUAEh+XVf7V53R67Ypz9VYzH3JWZghr8qi1PV34KxOisMFTRXIp6upAgmZTBdpuuJm34MHo90PpmugOiUxSyXljAlBGJUQJfuwIwiNlUyZSIVQInUlrc+1Cz2uYqawTKRIhEqSFGrP/h1bhAfJZnswkN6Zg+6rrixOv9/0r5qqOCDhlX+tWzt0vnOAzNg5lT6rV5XxDuLDGspyvs6a3U3wDBZ4vd23MMNBfrbyoCNIDFCIgGAcMxiFCDTuYgcq7Gmwp8CTq5XFYZ+k1FP4MQujpwLfDVcbFSWTlgRPYsrepzMcnQWNd3xX5Ie6tNfTxJb5+qipo/9q2GTm4D7nLMnvxHIxv3Cvxdp0talGbwZDDs3Qh+A8cfTC5OUGpmFjBEQ7Y30LFwirhVl1Zrp35XuyAJffxaeOem/Zs/q8azZv6u1b8ISLCyzm0y0Xfd6VrfM3lEEFWJujTxVlr6GAFKfnXPiB6rkrFACPddBAYA72tgFTf/GfX9e6Rv+qoPPqbbkCHpBfgMJFYWU20HQh653N++sB9s98N+fwRU32I6S4C7Mc7QfbDzqec02kq/ZWu45vBKHSe9OdweL5fdkUl2CBLbxGEO9tsHVrTPCScF/4aIGdj62zfAXo92jnOndIDZADKFZU4TRRkAT2cK8YQ9sJ3YgUNIXeD1Z/Dm1+6HMdDC4Yz7J3WL2wKThaQPA9WL76+LGUMeZJymWSYObSaSo8liLGkjAMCVsIKVPMfhcs82az0XWBat8bXUNOio6lWmPnnEgTh2sAbbDThg6sRgb3zOLS2wF1/R6rnODwLrPg/90oR2hnNIbXEEt5Ck+WRCoA2WPLY04ZFUxIihPwX+KxnXGoUZKJhEoMxnCV7SJzW+go1vBs6n0rb8dC4j++KIvC+G4y1LWf6nCkDwnV7NqqzEv7FN9+/fH7No0lkYpyxRVLxi7CebxMOVGK4VQpwbn6A1z76w6S9KqpdfWAk78OTq7vOXn2BCfP/l+c/AFv3r/D9wFmRmKeppxCD0YVJUSxP97Lz01zUzXtpUXum2L9uCnqYWO6Mj+gvfYMAaFhwimWCVVpQqCLDU4YRPyWeDq1F/lAe91r/z4U3qcBmN0H8N/kiRDCgQsQZ+AsSpLjP5x8xCiCe3ZwwqW08bLw+ioiBOugPfo7cgj41+jjQPlT95HCT1T78au9NTtLxrv97aehsf90Yoe1BdXCHP0DuSUYwjz8fUgBePUey0pg/FfmLv9e7wHS5fFtOz3ep1QykvZWd/Ybl/qRy3UsxgmBB6kSGDpPSplPdSpW3L0uoXhDWYHyfVpPTlGenzb0/sk8/u/vy/8CUEsHCJp/FVf7BgAAmhYAAFBLAQIUABQACAgIANy8ZUBFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgA3LxlQJp/FVf7BgAAmhYAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACTBwAAAAA=" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

SimonS - parallella och vinkelräta linjer

Parallel Lines

http://www.youtube.com/watch?v=nZuko8vyVs4

Load video
YouTube

http://www.matteboken.se/lektioner/matte-2/funktioner/linjara-funktioner-y-=-kx-plus-m

Ytterligare en sida för dej som fortfarande inte förstår vad det handlar om.

http://www.malinc.se/math/functions/perpendicularlinessv.php

Fin sida för dej som satsar på högre betyg på provet än E/D. c:

Allmän form (linjens ekvation)

s. 113- 115

Det kan vara bra att ha sett detta men vi kommer att göra detta avsnitt kursivt och skynda vidare. Det är nämligen dags att göra Veckodiagnos 17.

<ggb_applet width="571" height="319" version="4.0" ggbBase64="UEsDBBQACAAIACmAaUAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIACmAaUAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1sxVfrjtQ2FP4NT3GUSvxidmLnOjADWpBQkRaKtLSq+s+TeGbMJnGInbkgHqdv0hfrsZ1kkoVCWVA72lnH9sm5fOc7x57l02NZwJ43Sshq5ZEL3wNeZTIX1XbltXozS72nT+4vt1xu+bphsJFNyfTKC42kyFdeuqbBJufJzI8iOguTjT9Lk5jMcC3MUpYkYRR6AEclHlXyNSu5qlnGr7MdL9mVzJi2hnda14/m88PhcNGbupDNdr7dri+OKvcA3azUyuseHqG6yUuHwIpT3yfz319dOfUzUSnNqox7YEJoxZP795YHUeXyAAeR693Ki5KFBzsutjsTU0w9mBuhGgGpeabFnit8dTS1Meuy9qwYq8z+PfcExRCOB7nYi5w3K8+/oAlN05CmAQ3jRZJEkQeyEbzSnTDpjM57dcu94Aen1zxZk4ihlrJYM6MSPn4E6lMfHpqBuIHiEMduy3drfuAG6obQDZGTCd3roRMNnUzoZMLAg71QYl3wlbdhhUIIRbVpMH3DXOlTwa0/3cI5fPIQY1LiAwoHPvLEYY7rvv/QfGP8hmZjPg2SjKzqpv1Go73J0E//vUn6PSaD3iSJPmOSRv8QZfwFcJ0P/yZMEo2QRVP2z34/sRjQb7Do5t9nMA7/kxCX875Sll1xgNoZ2S6TmpfKlEuwgGhhWE8gwtKIEyR5BGSBQ0IBiwFIBGGEU5JCbMYEggQ3QgggBSNHArC1EaX4L0ysshgiVGZWEyxJIGgohCgAYksqBCwksGWJJUoDlIgiiPAlY55QoyKIIYxxFqQQoo+mIhOCggG+iHM0TyEgEJiXSQI0htjoI6Gp9Dg1rqNKCrEPMTEKsaixoF0xo3wKgYkm7uASVd3qCURZmfePWtZDLlAa29G567n2NGmK95YFW/MCz4lrk0mAPStMRVhDG1lp6JMYu7Vtw+qdyNQ11xrfUvCO7dkV0/z4AqVVb9vKZrJSbxqpn8uiLSsFkMnCH3yWBRk908FrnASjjXC8EY024tFz8lm7EnegVRzty0b14izPXxqJc2tAJH+pitOzhrObWoppGMu5PXKWvM0KkQtW/YZkNVYMLtCfQLZb9ScQXcS9I7LJr08KGQzHP3gjV94iMEfuyU1oggfw+IMpVhkz5Rb5Vm40G3+o08/3QxrYkQ8RbhtTvV10ZvJSPZPFecnG+JzVum3sBQH7SmM8v6y2Bbc8sNWLp292s5bHa0eAwOl6e6px5jsH1luLLWD9U3Mibrtx7UYrYzwbpHwr41sJv2eUyId9sqBWwo5rN1oppKhzrYuU9GESvzcjlO1avjepDctvc5a3ldBX/USL7OYcqZF/3ZZrPrBkqpL8IJXL+S0WLW94U/GiIy1mspWtcjU44nPOM1Hi1G10gDCTrF/RAbea823De78Le/VycNldf8zHT5atqheNLF9W+7fIhFsOLOe9l0uVNaI2hIM1NvobfuZULhTDcyIfv2eqDEPPzHmA8GgDDdZfq3eysbcrbBs4WsmyZFUOlT1a3hh+eudWx7BpnC4xGc5d2ep+9dL5171uqrTgJd7JQFuWWqIP+bq0Kk1iQK7fYQu8lc9z4nH7zEjqeG3HjtfAinrHzK2wQ7BgJ95MMLU6X8n8NtKYSAsH9oTaEaXm3FHM+YwPNaqzhTnpaZg6BUdnFE7YpM34wd323XXXRGuK1ZmMx6u3co5EdEB9BbJnd4JsXOT/O1xhB1f0g+CaUvUK29Itpl5ivMRAd5us7MtkNR1uAJZ9BfhRqBOyRsEI+4jcHfozgDPaIRh2CM4IHbQNXVnjpeAGf/gog2QXke8efhZ5zu2F0B1a7yv3inLNkh/rQmRCf8LLY92gPpP9Lui3/KgxJNxYeQ/et1I/pqfZcRav/Ac/Ef8xK4ryrz+ryv66dftW5xRmvKmc+e003gnq6Ul2Z5ztHUvxRmzO95H+wtUj1Inir+BG294IJi+kSwudEnsM4Xzcge1VpvtV/uRvUEsHCIPHZITNBQAAMhAAAFBLAQIUABQACAAIACmAaUDWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAKYBpQIPHZITNBQAAMhAAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAABkBgAAAAA=" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

Ekvationssystem (grafiskt)

s. 116-119

Två räta linjer = Ekvationssystem

Här har vi två ekvationer. Det är ekvationer med x och y. Var och en är en ekvation för en rät linje. De har skrivits på en form där variablerna (x och y) står till vänster och numeriska värdena (siffrorna) till höger.

Ekvationerna har döpts med ett nyummer som skrivs inom parentes, (1) och (2). Vi döper ekvationerna för att kunna beskriva hur vi jobbar med dem.

Det kallas för ett ekvationssytem:

<ggb_applet width="515" height="329" version="4.0" ggbBase64="UEsDBBQACAAIAFC4a0AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAFC4a0AAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVjrj9M4EP8Mf8UoJ6FDx7ax82qhBXFI6FZaHtJyp9N9cxK3NZvGIXFfiD/+ZuwkTbeAFrij2q7jzHjev/Hszp7t1wVsZd0oXc49NvI9kGWmc1Uu597GLC4m3rOn92dLqZcyrQUsdL0WZu6FxKnyuRfwNJZpzi+iVEwuwjzKLiYiYxfTOFvwIImkn3APYN+ox6V+LdayqUQmr7OVXIsrnQljFa+MqR6Px7vdbtSpGul6OV4u09G+yT1AM8tm7rUPj1HcyaFdYNm577Px36+unPgLVTZGlJn0gFzYqKf37812qsz1DnYqN6u5F/HAg5VUyxX5FIcejImpwoBUMjNqKxs8Othan8268iybKIl+zz1B0bvjQa62Kpf13PNHfML8xE/CKJ4mk2mcRB7oWsnStMysVTruxM22Su6cXHqyKtEyo3WRChIJnz4B97kPj2hhbuG4xLEj+e6dH7iFuyV0S+R4Qnc8dKyh4wkdT4hR2apGpYWcewtRNBhCVS5qTF+/b8yhkNae9sXRffYIfWrUR2QOfKwTF3N87/uP6BvjNyTC+NRJNtBq6s03Ku1VxsHdVfIfURl0KlmYnKvk0Re8jL8SXGfDXdxk0SCyqMr+2O+ZxoB/g0a3/zGFBKSf4OJs3CFl1oIDmhXxtpk0ct0QXIIpRFOqegYRQiNOsMgjYFNcEg4IBmARhBFu2QRiWhMIEiSEEMAEiI8FYLERTfBXmFhhMUQojN4mCElgqCiEKABmIRUCAgksLBGiPECOKIIID5F6xklEEEMY4y6YQIg2EiIThowBHsQ9qucQMAjoMEuAxxCTPBYS0uMJmY4iOcQ+xIwEIqgR0A7MyD+BgLyJ23CpstqYkxBl67x7NLrqc4Hc2I6OXc+1p5OmeG9WiFQWeE9cUyYBtqIgRFhFC10a6JLI3btlLaqVyppraQyeauC92IorYeT+JXI3nW7Lm+myeVtr80IXm3XZAGS68HubdcEGz7y3GjfBgBAOCdGAEA+ek8/q1UiBTSNRv66bjl3k+SVxHFsDRvJNWRx+r6W4qbQ6dWM2tlfOTG6yQuVKlH9hsZIWigt0N5DtVt0NFDDWGaLr/PrQYAXD/h9Za4xjMB35w8/Ug4Mj8SQcTQefCTWmTBD4Iv/0EFIOLSmcnhyaTmKnW277FIm97L1f1oTs1nPaXDa/6+L4yvr/QlRmU9vhATXV5NXzcllIWyMW2XgzZzep3l+74gicrHeHCne+MyBd2rgD9gYe4W25bNfUrZaHLOu5fMvjWw6/qzaV93Q25ZbDrqlbLReWrzOt9ZR1bjK/U6Ma29F87wQ3tvbpnt+Uylx1G6Oym6OnxP96s05lX0GnItl/JHI2vlVhsxtZl7JoCxozudGbxuFzUOu5zNQat47QBkRQsv5EA9zbXC5r2dld2LHMhctS/WGtnr22ol7Wen1Zbt9hJdwyYDburJw1Wa0qKjhI8RK4kceaylUj8A7Jh+cIgeh6RncFhsdQaBCbG7PStZ28sKXgSsAr5BrHLDC2uCjXfZSFnd8onKDT99jUbmXhmC4kf7bOcEhCrUW1EjTjtT4X4iDrkyhYeW8Wi0Ya2CMoCH9zD6fqI/WVzuWtJGBirHuI/4rEU+orKV3RmBYrUKE6C7WTDobJaEiVneUP7foRdfLeyr7qDTbkGxw6sZqigWB6+EPlubSXsWsKH0p3pHHFqNZVoTJlWq0Ie7LXevEre9iWpYv/1zORflcmur7QYf67MxH//4m4OMtE+LMywc8yken1WpQ5lHYUuywNthIMunccD4RP8ADBKDcu8BvTEZ47ea2Us8zaO6BP3fPvSi3Njku3pG65Y26P6fPPUsDbFMRtCnosWIvpLnInk+HbY0vjZwW9r2pMFkW6dead3BusCSTMvQcfNto82f92mHOgDyLiwS/Mf3K42M9DcK/4Q8dlJZ9GEUeiYxCd3K8HclB2X2pXd4fIWRjtMNfIWi2Og4+7vGOvK8KWFf/crs1bCh5Q2P3RJD6ZPphNQjDi7HTysDlhzrBhmMfDZm8nqvafA0//BVBLBwiaXODO+wUAALkQAABQSwECFAAUAAgACABQuGtA1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAFC4a0CaXODO+wUAALkQAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAkgYAAAAA" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

Man kan lösa ekvationssystem och få fram vilken punkt som gäller för båda ekvationerna. man kan lösa detta algebraiskt eller grafiskt.

Grafisk lösning sid 116 nedre delen, motorcyklar:

<ggb_applet width="792" height="457" version="4.0" ggbBase64="UEsDBBQACAAIADVUbUAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIADVUbUAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVdbb9s2FH5uf8WBnuOYpK4J7BZpgWIB0nZYsmHYGyXRNmtJ1ET6VvTH75CUbDnNit62oglF8vDcvvMdMrOX+7qCrei0VM08oJckANEUqpTNch5szGKSBS9fPJ8thVqKvOOwUF3NzTyIrKQs5wFZsJwKnk6YuGKTKEuiSUbScJLnIluEkQhJVgYAey2vG/WO10K3vBD3xUrU/E4V3DjDK2Pa6+l0t9tdDqYuVbecLpf55V6jAnSz0fOg/7hGdWeHdqETZ4TQ6Z9v77z6iWy04U0hArAhbOSL589mO9mUagc7WZrVPMgIhrEScrnCmBI7mVqhFhPSisLIrdB4dDR1MZu6DZwYb+z+M/8F1TGcAEq5laXoMD+XLA5AdVI0pt+lvZXpcH62lWLnFdkvZyMKwChV5dzqgE+fgBFG4MIO1A8MhyTxW8SvkdAPzA+RH2IvE/njkReNvEzkZaIwgK3UMq/EPFjwSmPOZLPoEK/jXJtDJZw//cIpXnqBMWn5EYVDm0SfZFwn5ML+YGYvoiG7oyDpyKrpNt9odDAZZ+nXm2Q/YjIcTLKnomTxv0SZfCG53oevCZPGI5toyv13P59ZDNk3WPTzHzOYRP9LiLPpwJRZTw7QKyvbI2lErS1dwiuIr2zVU4iRGkmKRR4DvcIhZYBkABpDFOOUZpDYMYUwxY0IQsjAytEQHDfiDH9FqVOWQIzK7GqKlASKhiKIQ6COUhEgkcDREinKQpSIY4jxkDVPmVURJhAlOAsziNBHy8iUomCIB3GO5hmEFEJ7mKbAEkisPhpZpieZdR1VMkgIJNQqRFIjoT2ZUT6D0EaT9OmSTbsxZykq6nL4NKo9YoHS2I5Obc63p7Mu+GxW8VxUeDHcWyQBtryyjHCGFqoxMICY+LVlx9uVLPS9MAZPafjAt/yOG7F/g9J6sO1kC9XoXztlXqtqUzcaoFAVOfqsKjr6ZkevcRKONqLxRjzaSEbf6ZN2Fe7ARgu0rzo9iPOyvLUSp9aAmXzfVIdXneDrVsnzMGZTd8fMxKaoZCl58wcWq7Vi8wLDleO61XDlRGE0OKK68v6gsYJh/5foFPYYFl6S8T/sPge/FWbkbAtvGF1wyz2W2Yv50M/w8knYuaCzJrZHUPheHONddpbLfax2cqtfqeq05CJ+zVuz6dz7AB3qbBw3zbISriocl/HyLda52t/7cgi9rodDaz3yDuRLl2nAbsBi9H7Zj7kfnYz17ChFnAxxEmSoL1ke9+kVcxJuzP3opLBgvWt9pHQIk5LBjNT+JROcMcVVu73KN400d8PEyGJ9itTKv9vUuTjWzLlK+pNUzqaPamq2Fl0jqr6EEcmN2mjPyFF1l6KQNU79Rp8QbsH6HR3wq6VYdmLwu3IvL58ut0vG1fnZslP1plP1bbN9wEp45MBsOng500UnW1twkGPbX4tTTZVSc7w1yvE5yzkMvbC3A6bH2NQgGzdmpTr3uMImgqOlWiVqfFiBccVlsT5mmbsnmk0nqPwDtrFHKJzgwu1TNZLorNKAV+2KWyb1MVf8ILqzLDh97xcLLQzs58GEoYYDjkky2n+rSnHWMXmD0LgAkfOtNWDBb4XwZWN6tkCLBh3ZzroWwqGdsZQ4vvdP94/WPDn5eqx9g414jY9NrKl0pNx+/CLLUrhL2LeGvxt/RPuSFPu2koU0vWUkv/XZRXLPa9Drjj883PzWV6mH48vA5N8FzLgBOJC+GZiox4VdPYkL+6m4hPFjXKL4P8NlnPhC1TVvSmjc0+u2MdhIMMfB6TnAiSUHcGqh8HnemGHjxuvrtXwGpLsBjkjdfBeSlPStmrDvJpmHMk6fRJI+RoPFA0sYokB6RBxE/s89G5W9rfz5dLz6qOmNUz0d9yl3/fd/ur74B1BLBwh3CgwTiQUAAFcPAABQSwECFAAUAAgACAA1VG1A1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIADVUbUB3CgwTiQUAAFcPAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAIAYAAAAA" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

KevinS - ekvationssystem

  • En film av Matteboken, Bondestam etc
  • En Khanlänk
  • En text
  • En definition
  • Ett exempel
  • En uppgift
  • En bild
  • En länk till fler förklaringar
  • En länk som knyter ant till matematikens kulturhistoria
  • Ett försök att förklara vad man ska ha detta till

Ersättningsmetoden

s. 120-122

Här finns det plats för Håkan att skriva om annat som ska hända på lektionen än just det som som eleven nedan förbereder.

PatrikS - Ersättningsmetoden

Additionsmetoden

s. 123 -126

Här finns det plats för Håkan att skriva om annat som ska hända på lektionen än just det som som eleven nedan förbereder.

RichardS - Additionsmetoden

Additionsmetoden kan användas för att lösa ett ekvationssystem med två ekvationer och två obekanta variabler x och y. Man måste då eliminera en av de obekanta variaberna genom att multiplicera ekvationerna med lämpliga tal så att antingen x eller y försvinner om man adderar ekvationerna.

x + y = 5, 2x − 3y = − 5 Om man vill eliminera x kan man multiplicera den övre ekvationen med -2.Det ger då att − 2x − 2y = − 10 Om man sedan adderar vänsterleden och högerleden får man att − 2x − 2y + 2x − 3y = − 10 − 5 Det ger att − 5y = − 15. Om man löser ut y får man att y = 3. Man kan sedan sätta in detta y i en av de ursprungliga ekvationerna. Om man väljer den första får man att x + 3 = 5 och det ger att x = 2. Lösningen till ekvationssystemet blir x = 2,y = 3

Wikipedia

Här är en bra video som visar hur Additionsmetoden fungerar: 

http://www.youtube.com/watch?v=ZIHb8YyeMco

Lösning till ekvationssystem

s. 127- 128

Här finns det plats för Håkan att skriva om annat som ska hända på lektionen än just det som som eleven nedan förbereder.

JakubW - Lösning till ekvationssystem

Problemlösning med ekvationssystem

s. 129-132

Ekvationssystem med tre obekanta

s. 133-134

Repetition

När du repeterar tänker du kanske: - Vad ska jag ha denna algebra och geometri till?

Se filmen så får du svaret;:

Load video
YouTube

Prov algebra och geometri

Här kommer en annan typ av test. Mashmallowtestet!

Load video
YouTube


Hämtad från ”https://wikiskola.se/index.php?title=Geometri_2C&oldid=12431”