Rörelse: Skillnad mellan sidversioner

VisuellWikitext

Versionen från 13 december 2011 kl. 15.23

Lektion 4 - Rörelse

Wolfram Demo Galileo lutande tornet i Pisa.

Vi behöver jobba färdigt med SI-enheter, sid 21-23.

Länkar

Hastighet enligt Wikipedia

Innehålll

Föremål i rörelse

Film Min film men pingisbollen på Youtube: http://www.youtube.com/watch?v=OYuJXnwDPIE. Men det blir bättre med MovieMaker för där visas tiden i hundradelar.

Beskriv rörelsen med ord Beskriv diagrammet Försök Göra en kurva med hastigheten.

Förklara hur man går till väga när man räknar ut hastigheten med hjälp av mätpunkter i Excel.

Hur långt hann vi? DEDT10 han göra v-t-kurvor men vi hann inte med att diskutera dem. Ska de vara räta eller ... ? Samma ungefär med NV, dock ej vt-kurvor alls.

Ventenskapshistoria

Nicolaus Copernicus, 19 February 1473 – 24 May 1543)
Tycho Brahe, (14 December 1546 – 24 October 1601),
Galileo Galilei, 15 February 1564– 8 January 1642
Johannes Kepler, December 27, 1571 – November 15, 1630)
Sir Isaac Newton (25 December 1642 – 20 March 172

Länkar

Film

Genier, Darwin, Newton, mm 88 min. Bara på dvd.
Den rörliga jorden, 51 min.

Lektion 5 - Medelhastighet, vektorer mm

Repetera S-t-diagram och medelhastighet s 24-26, 30-32. Vi tittat på våra diagram från filmen. Vi räknar ut medelhastigheten ∆s/∆t.

v_m = ∆s/∆t

Hastighet som en vektor, s 28-29.
- Fart är hur fort det går i vardagligt tal.
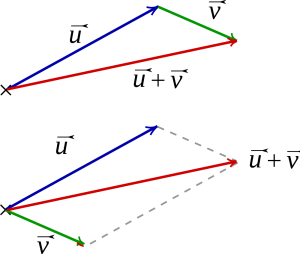
- Hastigheten har en storlek och en riktning. Den ritas som en vektor.
Vektorer kan adderas och subtraheras.
- PPT om vektorer som presenterar bokens exempel med fågeln.
Gör arbetsblad vektorer. Formelsamlingen sid 13 definierar trigonometrin f rätvinklig triangel.
- Resultant och komposant

Film

Isaac Newton och gravitationen - Milstolpar inom naturvetenskap och teknik, 15 min. Den börjar med de gamla grekerna, uppehåller sig länge vid Newton och berör Einstein. TEDT hann inte se den.

Gör den här övningen med vektorer!

Lektion 6 - Hastighet

Repetition: Forts genomgång av extrabladet om vektorer.

Idag gör vi sid 30-32.

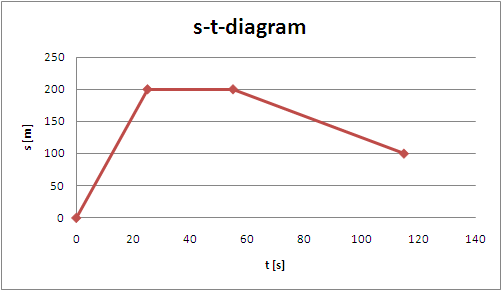
Sträcka-tid-diagram

Att utläsa hastigheten ur diagram.

∆s
∆t
v_m = ∆s/∆t (som vi vet sedan tidigare)
brantare lutning är högre hastighet
vågrät = stillastående
avtagande lutning betyder att färden går tillbaks

Bokens Exempel 3.5: Gå igen detta och förklara vad en tangent är. En applet förklarar

Uppgifter: Gör uppgifternas 308-312 på sidan 32. Lösning i Excel till uppgift 310

Datorövning: titta på s-t-diagrammet med pingisboleln igen.

Excelfil med pingisdata.
Beräkna medelhastigehten för hela resan.
Hur ändras hastigheten under bollens färd?

Datorövning: Movin Man från PhET Colorado

Click to Run

Lektion 7 - Acceleration och vt-diagram

Bedömningsmatrisen för densitetslabben

Planering: Vi behöver bestämma datum för laborationen om acceleration. Förslag:

TEDT10 onsdag vecka 39 kl 10.40-12.10 Den halvklassgrupp som har operativsystem denna onsdag
TEDT10  onsdag vecka 40 kl 10.40-12.10 Den halvklassgrupp som har operativsystem denna onsdag
NVNV10 tisdag kl 8-9.30 vecka 39. (NV10 ledigt)
NV10 onsdag kl 12.40-14.10 vecka 39. (NVNV10 ledigt)

v 38 Genomgång idag: neXus FYSIK sid S 33-38.

Acceleration

Medelaccelerationen = ∆v/∆t
- ∆v = v_efter-v_före
- ∆t = t_efter-t_före
Acceleration enligt Wikipedia.
Gå igenom exempel 3.8 i boken.

Tyngdaccelerationen

Tyngdaccelerationen är cirka 9,82 m/s² vid jordytan. Eftersom jorden är plattare vid polerna ökar tyngdaccelerationen ju längre norrut vi kommer från ekvatorn.

v-t-diagram

vt-graf Wikipedia.
- Här kan man jämföra st- och vt-grafer. Motsvarar Exempel 3.9 i boken.
Lutningen i vt-diagrammet visar accelerationen:
- brantare lutning <==> större acceleration
- lutar "neråt" <==> retardation

Datorövning:

titta på filmen med pingisboleln igen.
Använd ditt s-t-diagrammet med pingisbollen igen till att skapa ett vt-diagram. Är rörelsen accelererad? Excelfil med pingisdata.
Räkna ut medelaccelerationen. (Detta motsvarar exempel 3.7)

Mer att titta på:

Lektion 8 - Begynnelsehastighet - formler för s och v

v 38 Idag: Sid 39-44

Laborationsinstruktion: Gå igenom instruktionen till Acceleerationslabben

Begynnelsehastighet och förändring av hastigheten

Acceleration är lika med hastighetsökningen per sekund. Vid en konstant acceleration a, gäller då att:

v = v₀ + at

v₀ är hastigheten vid start och t är så klart tiden från start.

Exempel: Fru Gran tapper en blomkruka genom fönstret. Vilken hastighet har den 1,5 sekunder senare?

t = 1,5 s. a = g = 9,82 m/s². 
v = at = 9,82 m/s² * 1,5 s = 14,7 m/s

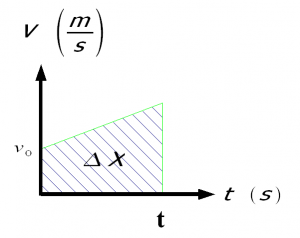
area

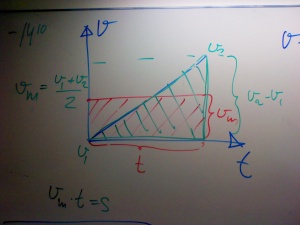
Arean under en vt-graf är lika med sträckan. Tänk att medelhastigheten * tiden = sträckan.

v_m = (v_efter - v_före) / 2

Men sträckan är ju v_m * t och det kan man ju se som arean av cen triangel som bildas av grafen i vt-diagrammet.

naturvetenskap.org ger en beskrivning.

Animering av sträcka under vt-kurva <swf width="600" height="400">/images/FysikA_s_e_area_u_vt_kurva_2.swf</swf>

sträcka

Härled uttrycket nedan som på sidan 41.

s = v₀t + at²/2

Extrablad: Rörelselära ... Och Övningsuppgifter på hastighet och fart.

v 39

Sid 45-53

Uppgifter: 320-327

@@ Rad 1: / Rad 1: @@
 == Lektion 4 - Rörelse ==
+[http://demonstrations.wolfram.com/GalileosExperimentAtTheLeaningTowerOfPisa/ Wolfram Demo Galileo lutande tornet i Pisa].
 Vi behöver jobba färdigt med SI-enheter, sid 21-23.