Cosinussatsen: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
||
| Rad 1: | Rad 1: | ||
__NOTOC__ | |||
= Teori = | |||
{{#ev:youtube|yKBLBZ_Thts |240|left|Cosinussatsen}} | {{#ev:youtube|yKBLBZ_Thts |240|left|Cosinussatsen}} | ||
| Rad 38: | Rad 41: | ||
#: c<sup>2</sup> = a<sup>2</sup>+b<sup>2</sup>-2abcosC | #: c<sup>2</sup> = a<sup>2</sup>+b<sup>2</sup>-2abcosC | ||
<br /> | <br /> | ||
= Lär mer = | |||
{{svwp|cosinussatsen}} | {{svwp|cosinussatsen}} | ||
<br /> | <br /> | ||
Versionen från 17 mars 2019 kl. 18.53
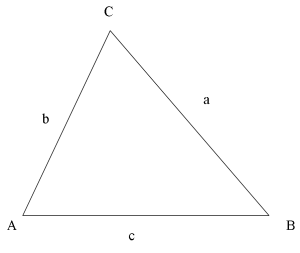
Teori
Om sinussatsen inte fungerar kan du prova cosinussatsen.
Nu har du lärt dig de tre triangelsatserna; areasatsen, sinussatsen och cosinussatsen.
| Definition |
|---|
| Cosinussatsen |
Härledning

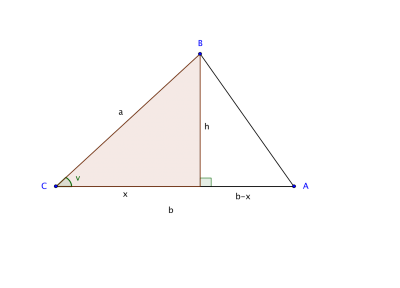
- Rita in en höjd i den vänstra triangeln så att det bildas två trianglar som i den högra bilden ovan.
- Använd Pythagoras för de båda trianglarna
- x2+h2 = a2 (1)
- (x-b)2+h2 = c2
- Förnkla uttrycket ger
- x2+b2-2bx+h2 = c2
- Stuva om i termerna
- x2+h2 = 2bx + c2-b2 (2)
- Sätt x2 + h2 lika. Ekvation (1) i ekvation (2)
- a2 = c2-b2+2bx
- Använd att x = acosC ger
- a2 = c2-b2+2bacosC
- Stuva om så att c2 står fritt ger
- c2 = a2+b2-2abcosC
Lär mer
Wikipedia skriver om cosinussatsen