Versionen från 23 september 2018 kl. 18.57

Inledning

Mål för undervisningen Talmängder

Du ska lära dig vad som kännetecknar naturliga tal, heltal, rationella tal, reella tal och komplexa tal.

Vi kommer särskilt att öva på räkning med negativa tal och bråk.

Swayen till detta avsnitt: Talmängder

Läs om Tal

Teori

Tal

Tal är ett matematiskt grundbegrepp som används för att representera olika storheter, det vill säga sådant som går att mäta i bestämda måttenheter, till exempel antal, längd, vikt, volym, temperatur och tryck.

Ett tal är en abstrakt enhet som representerar ett antal eller ett mått. Inom matematiken är definitionen av tal vidare och inkluderar bland annat naturliga tal, heltal, negativa tal, rationella tal, reella tal och komplexa tal med mera.

Aritmetik (räknelära) behandlar räknande och innefattar grundläggande egenskaper hos tal, som hur de skrivs och hur de fungerar under addition, subtraktion, multiplikation och division; även andra räkne-operationer som procenträkning, potenser, rotutdragning och logaritmer tillhör aritmetiken. Hur vi hanterar tal, hur de skrivs och vilka egenskaper de har, ligger under aritmetiken.

Algebra kan definieras som en utvidgning av aritmetiken och kan beskrivas som förhållanden, vilka uppkommer, när ett ändligt antal räkneoperationer utförs på en ändlig mängd av tal. Algebran ger oss en metodik för hur tal förhåller sig till varandra.

Tal ska inte förväxlas med siffra eller nummer som har helt andra funktioner. Ibland kallas räkneuppgifter för "tal", då i meningar som Löste du talet?

Talmängder

Tal brukar delas in i fem grundläggande mängder (grupper). Det ger oss kategorier där talen har liknande egenskaper:

Grundläggande
[math]\displaystyle{ \mathbb{N} }[/math]	Naturliga tal	0, 1, 2, 3, 4, … eller 1, 2, 3, 4, …
[math]\displaystyle{ \mathbb{Z} }[/math]	Heltal	..., −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, ...
[math]\displaystyle{ \mathbb{Q} }[/math]	Rationella tal	[math]\displaystyle{ \frac{a}{b} }[/math] där a och b är heltal och b inte är 0
[math]\displaystyle{ \mathbb{R} }[/math]	Reella tal	Gränsen för en konvergent följd av rationella tal
[math]\displaystyle{ \mathbb{C} }[/math]	Komplexa tal	a + bi eller a + ib där a och b är reella tal och i är imaginära enheten

De naturliga talen är en delmängd av heltalen det vill säga alla naturliga tal är även heltal, skillnaden i detta fall är dock att heltalen även innefattar negativa tal. Heltalen i sin tur är en delmängd av de rationella talen, de rationella talen är en delmängd av de reella talen, och de reella talen är en delmängd av de komplexa talen.

Naturliga tal

Prioriteringsregler

Naturliga tal är de icke-negativa talen {0, 1, 2, 3, …} eller alternativt de positiva talen {1, 2, 3, …}. Den förra definitionen är vanlig i Sverige och allmänt i matematisk logik, mängdlära och beräkningsvetenskap, medan den senare kan hittas i bland annat amerikansk litteratur och bland talteoretiker.

Mängden av de naturliga talen betecknas ℕ (eller, av vissa typografiska skäl kan ett vanligt N i fetstil användas).

Enligt den definition som görs i Matematikterminologi i skolan, utgiven av Statens skolverk i Sverige, ingår talet 0 bland de naturliga talen. Konventionen att räkna 0 bland de naturliga talen förekom inte alls före 1800-talet och tillämpas inte av alla matematiker.

Heltal

Heltal innefattar talet noll (0) samt de positiva och negativa talen {…, −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, …}. Mängden av heltalen betecknas ℤ (eller, av vissa typografiska skäl kan ett vanligt Z i fetstil användas), från det tyska ordet Zahlen (som betyder "tal").

Mängden av heltalen är uppräkneligt oändlig.

När det gäller datorsystem används termen heltal (de hela talen) som distinktion till flyttal (de reella talen) eftersom de i datorer hanteras, beräknas och lagras olika.

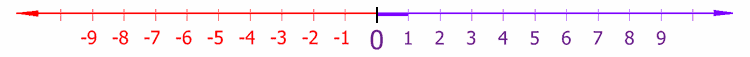
Rationella tal

Rationella tal, "bråktal", är de tal som kan skrivas som en kvot (ett bråk) av två heltal:

[math]\displaystyle{ \frac{T}{N} }[/math]

där heltalet T är bråkets täljare och heltalet N bråkets nämnare.

Mängden av de rationella talen betecknas ℚ (eller, av vissa typografiska skäl kan ett vanligt Q i fetstil används).

Irrationella tal

Irrationella tal är tal som inte kan uttryckas som bråk, det vill säga tal som inte kan skrivas som a/b, där a och b är heltal. Dess motsats är rationella tal. De irrationella talen är de tal som på decimalform har en oändlig följd av decimaler som inte består av ett oändligt antal periodiska upprepningar. Därav är pi ett exempel på ett irrationellt tal. Informellt uttryckt är nästan alla reella tal irrationella

Reella tal

Reella tal innefattar de tal som man vanligtvis menar med tal. De kan beskrivas som alla punkter på en kontinuerlig linje, utan att det finns glapp mellan talen i linjen. Denna linje brukar kallas den reella tallinjen.

Mängden av de reella talen betecknas ℝ (eller, av vissa typografiska skäl kan ett vanligt R i fetstil användas).

Aktivitet

Inledning

Namnrunda + bästa matematikområdet. Tänk på ett tal mellan 1 och 10.

Rationell betyder föenuftig, se Wiktionary

Vi kan representera tal genom att placera oss på olika sätt i klassrummet. Varje övning följs av en diskussion där vi lyfter fram olika typer av tal.

Laborativ/fysisk matematik

Vi ska representera tal genom att placera oss i klassrummet.

Tallinje:
1. Ställ er i ordning utifrån vilket datum ni är födda. (0-31).
2. Antal bokstäver i förnamnet subtraherat med antal bokstäver i efternamnet.
3. Hur långa ni är.
4-corners. Vilket lag håller du på i svensk fotboll? (Djurgården, AIK, Hammarby, övriga).
Graderingslinje. Hur kul tycker du att matematik är? (0-100).
Stå upp - sitt ner. Reella tal - icke reella tal.

Tänkbara frågor och diskussioner

Tallinjen: om flera personer har samma födelsedag, hur ställer de sig då? I klump eller bredvid varandra? Har de ställt sig med ett prortionellt avstånd mellan sig där det är större lucka mellan representerade tal?

4-corners: Vad är hammarby för tal? Kommer eleverna fram till att de representerar rationella tal?

Graderingslinje Andra exempel på frågor kan vara ...

EPA

Hur många bilar måste Tesla tillverka för att leva upp till sitt börsvärde på samma sätt som exempelvis General Motors?

Uppgifter

Grundskolediagnos a

Till denna diagnos behöver du penna. Skriv svaret direkt på detta papper. Du får inte använda miniräknare men ställ gärna upp talen om du behöver. Det går på tid. Maxtiden är fem minuter Diagnos a

1. 234 + 908

2. 328 – 79

3. 5,67 + 1,87

4. 13,2 – 3,62

5. 14 + 6,7

6. 34 * 1 000

7. 7 * 62

8. 900 * 87

9. 7 * 6,9

10. 468 / 6

11. Bebbe, Tina, Paavo och Ritva vann 1 740 kr på tips. De delade vinsten lika. Hur mycket vann var och en?

Grundskolediagnos b

1. 261 + 2 963

2. 654 – 384

3. 6,66 + 12,5

4. 5,78 – 3,5

5. 20 – 12,2

6. 100 * 54

7. 478 *9

8. 45 * 50

9. 7,28 * 6

10. 288 / 4

11. Svenne, Gurra, Bettan och Sanna vann 1 360 kr på tips. De delade vinsten lika. Hur mycket vann var och en?

Facit finns också

Veckodiagnos 1

1. Vad blir 0,3 – 0,208

2. Varför är pi ett irrationellt tal?

3. Hitta på ett exempel där du använder orden äpple, frukt och äta eller gilla. Visa hur de två meningarna förhåller sig till varandra med en implikationspil.

4. Bevisa att medelvärdet på tre på varandra följande tal är medianen.

5. Vad är - 7 + (-8) ?

6. Beräkna 28 + (-3) + (-2)(-3)(-4)

7. Är 113 en primtalstvilling? Motivera ditt svar.

8. Är 12123 et primtal?

9. Förkorta så långt som möjligt 85/102

10. Vad är 9/5 / 3/20

Öva själv i en GeoGebra

Öva på Khan:

Missing Number

Classify numbers

Lär mer

Problems with Zero - Numberphile

Stora delar av texten ovan har hämtats från Wikipedia: Wikipedia skriver om Tal
Avrundning
Wikipedia skriver om Irrationella_tal
Wolfram Alpha om irrationella tal

Lång lista med väldigt många tal: What's special about this number?

Kluring

Vilken talmängd hör Pythonprogrammet till?

Exit ticket

Kunskapsmatrisen: Exit ticket: Taluppfattning

Tal och talmängder: Skillnad mellan sidversioner

Versionen från 23 september 2018 kl. 18.57

Innehåll

Inledning

Teori