Beroende händelse

Teori - Beroende händelser

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

Sannolikhet för beroende händelser, av Daniel Barker

Definition
Beroende händelser är när sannolikheten för en händelse är beroende (betingad) av vad som har hänt innan den aktuella händelsen. Exempelvis ändras sannolikheten för att dra en kula med viss färg om man tar upp kulor ur en burk utan att lägga tillbaks kulan. Man kan rita träddiagram för att visualisera händelser i flera steg.

Sannolikhetslära i flera steg

Först repeterar vi händelser i flera steg:

Exempel

Maria spelar fotboll och har under säsongen räknat ut att hon har en träffsäkerhet med 75 %. Alltså missar hon 25 % av gångerna hon skjuter mot mål. Hon ska skjuta tre bollar mot mål: P( två mål) Hon kan alltså: [Träffa, Missa, Träffa] [Missa, Träffa, Träffa] [Träffa, Träffa, Missa] Alltså tre möjligheter till att uppnå detta. Varje möjlighet har sannolikhet [math]\displaystyle{ (1/4 * 3/4 * 3/4) = 9/64 }[/math] att inträffa. Den totala sannolikheten blir därmed: [math]\displaystyle{ 9/64+9/64+9/64 = 3*9/64 = 27/64 }[/math]

Beroende händelser

Exempel

Tre vita, fyra svarta kulor finns en skål. Vi vill beräkna följande sannolikhet: P( vit, vit, svart) Totalt finns det 7 stycken kulor. Sannolikheten att börja med att dra en vit är då [math]\displaystyle{ 3/7 }[/math]. Efter att man har dragit den första kulan återstår det 6 stycken kulor. Drog man en vit kula är det då 2 stycken vita kvar av dessa 6. Sannolikheten att dra en vit då är [math]\displaystyle{ 2/6 }[/math]. Sedan finns det 5 kulor kvar, varav 4 stycken är svarta. Sannolikheten att dra en vit kula, följt av en till vit kula och slutligen en svart blir då: P( vit, vit, svart) [math]\displaystyle{ = 3/7 * 2/6 * 4/5 = 24/210 = 0.11 }[/math]

Från Wikibooks

Relativ frekvens

Definition
Relativ frekvens I statistik är frekvensen eller den absoluta frekvensen av någon händelse helt enkelt antal gånger som händelsen observeras i experimentet eller undersökningen. Dessa frekvenser åskådliggörs ofta grafiskt i histogram. Den relativa frekvensen är den andel av gångerna som händelsen observeras, det vill säga den absoluta frekvensen delat med det totala antalet observationer.

Wikipedia skriver om Frekvens

Aktivitet

Dra olikfärgade pjäser ur en skål

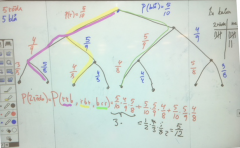
Demonstration:

1. Dra kulor ur urna.
2. Rita träddiagram på tavlan.

Exempel

Du kan använda nedanstående GeoGebra för att simulera ditt praktiska försök.

Ett pythonprogram för att simulera sannolikheten för fyrtal

Du kan ha nytta av den här typen av simuleringar om det är svåra beräkningar och du vill ha ett ungefärligt värde på sannolikheten som facit.

Lär mer

De Meres problem

Exit ticket

Exit ticket: Beroende händelse