Definiera trigonometriska begrepp: Skillnad mellan sidversioner

Från Wikiskola
Hoppa till navigering Hoppa till sök
VisuellWikitext
(Skapade sidan med '[https://gleerupsportal.se/laromedel/exponent-1c/article/9eee17ee-21eb-4f62-b32c-733e37bd6d23 Gleerups Inledning] [https://gleerupsportal.se/laromedel/exponent-1c/article/374c...')
 
Ingen redigeringssammanfattning
Rad 57: Rad 57:
{{Läxa|Lös uppgifterna 1201-1207 och gärna fler.
{{Läxa|Lös uppgifterna 1201-1207 och gärna fler.
}}
}}
{{flipp}}
 
== Exakta värden ==
 
{{lm3c|Trigonometri i Exakta värden|14-15}}
{{#ev:youtube| 03NICWDwUKA|240|right|}}
 
{{uppgruta|'''Vad är sinus 60°?'''
 
: Vad är det exakta värdet för sinus 60°?
: Du kan alltså inte svara med ett decimaltal från miniräknare.
 
: Hur härleder man vad sin 60° blir?
 
}}
 
{{#ev:youtube| 4C5j7EsWCB0 |240|right| |Sid 14-16 - Exakta värden för trigonometriska funktioner, av Åke Dahllöf}}
 
=== En halv kvadrat ===
 
::<math>\sin 45 = \frac{1}{\sqrt{2}}</math>
:
::<math>\cos 45 = \frac{1}{\sqrt{2}}</math>
 
=== En halv liksidig triangel ===
 
::<math>\sin 60 = \frac{\sqrt{3}}{2} = \cos 30</math>
:
::<math>\sin 30 = \frac{1}{2} = \cos 60</math>
:
::<math>\tan 30 = \frac{1}{\sqrt{3}} </math>
:
::<math>\tan 60 = {\sqrt{3} </math>
:
<br />
{{khanruta|[http://www.khanacademy.org/math/trigonometry/e/pythagorean_theorem_2 Special right triangles]}}
 
{{clear}}
<html>
<iframe src="https://docs.google.com/forms/d/1CWs7XDa3VuZVEB3jksHUzFgHn7ZyGGI8sNT3zkdk5Zs/viewform?embedded=true" width="760" height="500" frameborder="0" marginheight="0" marginwidth="0">Loading...</iframe>
</html>
 
{{Läxa|Lös uppgifterna 1218-1223 och gärna fler.
}}
 
== Avstämning vid slutet av lektionen ==
 
[[Kunskapskontroll Ma3C Fasta värden]]

Versionen från 21 juni 2018 kl. 10.59

Gleerups Inledning Gleerups:

Ma3C: Trigonometri i rätvinklig triangel, sidan 10-14
Load video
YouTube
Load video
YouTube
Load video
YouTube
Load video
YouTube
trigonometri i rätvinkliga trianglar, av Åke Dahllöf.

Trigonometri grundläggande

CC By
CC Wikimedia.org

Andra länkar om trigonometri

Definitioner:

  • Motstående katet
  • Närliggande katet
  • Sin v = motstående katet / hypotenusan
  • Cos v = närliggande katet / hypotenusan
  • Tangens v = motstående katet / närliggande katet

Digitalt

Definition: Ta reda på vinkeln

Om y = roten ur x så är 'y2 = x. Dessa två hänger ihop och den ena kan ses som den omvända av den andre. Detta kallas inversen, den inversa funktionen.

På samma sätt som det finns en invers funktion till kvadraten på ett tal, nämligen roten ur så finns det en invers funktion till sinus och cosinus. 

Om sin v = a/h då är v = arcsin(a/h) eller sin-1(a/h)
Om cos v = b/h då är v = arccos(b/h) eller cos-1(b/h)
0ch på samma sätt för tangens

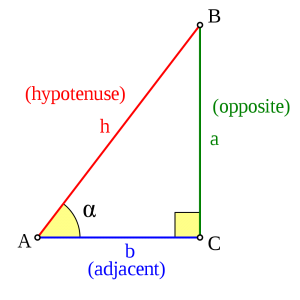
Den rätvinkliga triangeln

En rätvinklig triangel med hypotenusan c och katetrarna a och b.

En rätvinklig triangel är en triangel där en av vinklarna är 90 grader. Sidan som är motsatt den räta vinkeln kallas hypotenusa och de två övriga sidorna kallas katetrar.

Om ytterligare en vinkel är känd i en rätvinklig triangel är även den tredje vinkeln känd då en triangels vinkelsumma är 180 grader. Trianglar som har samma uppsättning av vinklar är likformighet|likformiga. Detta innebär att om man känner till en vinkel i en rätvinklig triangel är även kvoten mellan sidorna känd. Dessa kvoter ges av de trigonometriska funktionerna för en vinkel A, där a, b och c syftar på sidorna i triangeln i bilden till höger enligt:

  • Sinusfunktionens värde för en vinkel är kvoten mellan motsatta sidan till vinkeln och hypotenusan:
[math]\displaystyle{ \sin A = \frac{a}{c} }[/math]
  • Kosingsfunktionens värde för en vinkel är kvoten mellan närliggande sidan till vinkeln och hypotenusan:
[math]\displaystyle{ \cos A = \frac{b}{c} }[/math]
  • Tangensfunktionens värde för en vinkel är kvoten mellan motstående och närliggande sidas längd:
[math]\displaystyle{ \tan A = \frac{a}{b} = \frac{\sin A}{\cos A} }[/math]

Med dessa funktioner är det möjligt att (givet exempelvis en sida och en vinkel) bestämma alla sidor och vinklar i en rätvinklig triangel.

Texten i ovanstående avsnitt kommer från Wikipedia.se

Undersök

Aktivitet

Vi hämtar uppgifter från Diagnos sex finns här och Diagnos 7 finns här och gör cirkaövningar eller gruppövningar:

Metod

  • Cirkelövningar
  • Lämna vidare
  • Grupplösningr med muntlig redovisning
  • EPA
  • Spela in en film

Öva själv

Öva på Khan:


Ma3C: Trigonometri, sidan 10

Läxa! Lös uppgifterna 1201-1207 och gärna fler.


Exakta värden

Ma3C: Trigonometri i Exakta värden, sidan 14-15
Load video
YouTube
Uppgift
Vad är sinus 60°?
Vad är det exakta värdet för sinus 60°?
Du kan alltså inte svara med ett decimaltal från miniräknare.
Hur härleder man vad sin 60° blir?



Load video
YouTube

En halv kvadrat

[math]\displaystyle{ \sin 45 = \frac{1}{\sqrt{2}} }[/math]
[math]\displaystyle{ \cos 45 = \frac{1}{\sqrt{2}} }[/math]

En halv liksidig triangel

[math]\displaystyle{ \sin 60 = \frac{\sqrt{3}}{2} = \cos 30 }[/math]
[math]\displaystyle{ \sin 30 = \frac{1}{2} = \cos 60 }[/math]
[math]\displaystyle{ \tan 30 = \frac{1}{\sqrt{3}} }[/math]
[math]\displaystyle{ \tan 60 = {\sqrt{3} }[/math]


Öva på Khan: Special right triangles


Läxa! Lös uppgifterna 1218-1223 och gärna fler.


Avstämning vid slutet av lektionen

Kunskapskontroll Ma3C Fasta värden

Hämtad från ”https://wikiskola.se/index.php?title=Definiera_trigonometriska_begrepp&oldid=47217”