Primtal: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) (→Teori) |
Hakan (diskussion | bidrag) |
||
| Rad 111: | Rad 111: | ||
=== Definitioner mm === | === Definitioner mm === | ||
{{defruta| '''Primtal''' | |||
Primtal är bara delbara med ett och sig själva. (positiva tal) | |||
Alla positiva tal är uppbyggda av primtal (minst ett). Man dela upp dem i faktorer som är primtal. | |||
}}<br> | |||
'''Det kan vara bra att känna till att:''' | {{exruta| '''Det kan vara bra att känna till att:''' | ||
Ett helt tal är delbart med | |||
: 2, om sista siffran (entalet) är jämt eller 0. | |||
: 3, om talets siffersumma är delbar med 3. | |||
: 4, om det tal, som bildas av de två sista siffrorna är delbart med 4. | |||
: 5, när sista siffran är 0 eller 5. | |||
: 6, när villkoren för 2 och 3 både är uppfyllda. | |||
: 7, när talets tiotal minus dubbla antalet av talets ental är delbart med 7. | |||
:: Ex.:392 är delbart med 7 (39-4=35) | |||
: 8, när det tal, som bildas av de tre sista siffrorna är delbart med 8. | |||
: 9, när talets siffersumma är delbar med 9. | |||
: 10, när talets sista siffra är en nolla. | |||
Denna lista kommer från [http://matmin.kevius.com/delbar.php denna sida] | |||
''Denna lista kommer från [http://matmin.kevius.com/delbar.php denna sida]'' | |||
}} | |||
== Aktivitet == | == Aktivitet == | ||
Versionen från 5 april 2018 kl. 09.53
Teori
Pythonprogrammet hittar primtal
Intro - helklass

Primtalsorm (3-5 min)
Alla står upp Läraren säger ett tal till första eleven som svarar ja eller nej på frågan om det är ett primtal. Fel svar betyder man får sätta sig ner.
Diskussion: Hur vet man om det är ett primtal?
Fortsatta diskussioner - EPA m
- Exempel: Är 23 ett primtal?
- Exempel: Är 2310 ett primtal?
- Pröva själv på talen: 36, 114, 4007
- Demonstrera Wolfram Alpha
- Skapa uppgifter åt varandra
- Dela in tavlan i olika delar och låta dem komma fram och primtalsfaktorisera samtidigt.
Eratosthenes såll

Historik mm
När vi tittar på våra naturliga tal (alla heltal från 1, dvs. n = 1, 2, 3, 4, 5, 6, ...) så kan vi dela in dem i två grupper; Primtal, och sammansatta tal.
Våra sammansatta tal är alla tal vi kan skriva som en produkt av flera primtal. 12 = 2 ⋅ 2 ⋅ 3 15 = 3 ⋅ 5 Primtalen kan vi dock endast skriva med hjälp av primtalet självt och med 1. 3 = 1 ⋅ 3 7 = 1 ⋅ 7
1 är varken ett sammansatt tal eller ett primtal, utan är något som vi kallar för enhetselement (mer om det kommer inom den diskreta matematiken, framförallt på universitetet). Kort så är det ett tal som lämnar andra tal oförändrade under multiplikation.
De naturliga talen kan alltså delas in i: Enhetselementet: 1 Primtal: 2, 3, 5, 7, 11, 13, 17, 19, 23, ... Sammansatta tal: 4, 6, 8, 9, 10, 12, 14, 15, ...
Ordet prim kommer från latinets primus och betyder 'först'. Primtalen kan alltså ses som våra första tal, talen vi bygger upp alla andra tal med hjälp utav. Det finns oändligt många primtal, något som den grekiske matematikerna Euklides visade redan 300-talet fvt (före vår tideräkning).
Primatalsfaktorisering
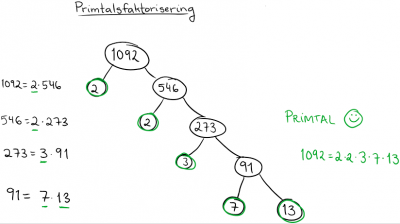
Vi vill nu primtalsfaktorisera talet 1092. Vi vill alltså skriva om talet i faktorer, tills dess att vi endast har primtal kvar. Stega genom våra primtal och kontrollera om det ingår i vårt tal, 1092. För att ta reda på det, måste vi kontrollera om 1092 är delbart med primtalet. Börjar med vårt minsta primtal, 2. Delbart med 2? Ja, talet är jämnt. 1092 / 2 = 546 Vi kan alltså utföra faktoriseringen 1092 = 2 ⋅ 542
Kan vi faktorisera 546? Börjar med vårt minsta primtal, 2. Delbart med 2? Ja, talet är jämnt. 546 / 2 = 273 546 = 2 ⋅ 273 Skriver om till 1092 = 2 ⋅ 2 ⋅ 273
Kan vi faktorisera 273? Börjar med vårt minsta primtal, 2. Delbart med 2? Nej, talet är ojämnt. Går vidare till nästa primtal, 3. Delbart med 3? Ja, siffersumman är delbar med 3 (siffersumman för 273 är 2+7+3 = 12, och 12 är delbart med 3) 273 / 3 = 91 273 = 3 ⋅ 91 Skriver om till 1092 = 2 ⋅ 2 ⋅ 3 ⋅ 91
Kan vi faktorisera 91? Börjar med vårt minsta primtal, 2. Delbart med 2? Nej, talet är ojämnt. Går vidare till nästa primtal, 3. Delbart med 3? Nej, siffersumman måste vara delbar med 3 (9+1 = 10, 10 / 3 = 3,3333...). Går vidare till nästa primtal, 5. Delbart med 5? Nej, talet måste sluta med en 0:a eller 5:a. Går vidare till nästa primtal, 7. Delbart med 7? Här har vi ingen snabb regel, utan får testa med kortdivision eller liggande stolen (eller miniräknare). 91 / 7 = 13 (Med kortdivision: 7 går i 9 en gång, 2 i rest, 7 går i 21 tre gånger, ingen rest) 91= 7 ⋅ 13 Skriver om till 1092 = 2 ⋅ 2 ⋅ 3 ⋅ 7 ⋅ 13
Kan vi faktorisera 13? Nej, 13 är ett primtal.
Vi väljer alltså att skriva om vårt stora tal, 1092, i dess primtalsfaktorer 1092 = 2 ⋅ 2 ⋅ 3 ⋅ 7 ⋅ 13 Nu kan vi mycket lättare hantera talet när vi behöver jämföra det med andra tal.
Definitioner mm
| Definition |
|---|
| Primtal
Primtal är bara delbara med ett och sig själva. (positiva tal) Alla positiva tal är uppbyggda av primtal (minst ett). Man dela upp dem i faktorer som är primtal. |
| Exempel |
|---|
| {{{1}}} |
Aktivitet
Öva själv
Kalkylprogram. Pröva gärna att använda Excel för att undersöka om ett tal är ett primtal.
Datorövning. Lär dig mer om ett tal genom WolframAlpha. Du ser bland annat hur talet delas upp i faktorer. Skriv bara talet på raden och klicka enter.
Datorövninga från matteva. Delbarhetsreglerna
Lär mer
|
|
|
|
|
|
Läs
- Wikipedia skriver om Primtal
- Här finns ett bra svar på engelska WP: https://en.wikipedia.org/wiki/Prime_number_theorem
- Om du tittar på den svenska sidan får du bara formler till svar: https://sv.wikipedia.org/wiki/Primtalssatsen
- Här ser du skönheten genom Ulam-spriralen: https://en.wikipedia.org/wiki/Ulam_spiral
Inspiration - En väl blandad kortlek är unik
Undersök och läs på
Blir det glesare mellan primtalen om man tittar på riktigt stora tal?
Exit ticket
Exit ticket: Primtal




