Geometriska satser och bevis ma1c

Teori

Definitioner

En rak vinkel är 180o

En normal är en linje som skär en given linje eller kurva i rät vinkel. "Rätvinklig mot" betecknas ⊥ (se figur 1).

Figur 1. Två vinkelräta linjer.
Den ena är normal till den andra.

Figur 2.
A: Cirkelsektor
B: Cirkelbåge

Fler definitioner:

Två linjer är parallella om de likbenägna vinklarna är lika stora.
Alternatvinklar
Sidovinklar
Bisektris

Satser

Vertiklavinklar
Likbelägna vinklar
Alternatvinklar
Sidovinklar
Thales sats

Vinklar i trianglar

Supplementvinkeln till en vinkel i en triangel kallas yttre vinkel.

Vinkelsumma

En linje som dras genom ett av triangelns hörn och är parallell med motstående sida, visar att triangelns vinkelsumma är 180 grader.

Sats

Vinkelsumman i en triangel är 180o

Radianer

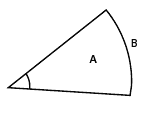
En vinkel eller ett vinkelområde är ett område av ett plan begränsat av två strålar, det vill säga delar av räta linjer som skär varandra i en punkt. Strålarna utgör vinkelområdets rand, och kallas för vinkelns ben. Skärningspunkten (och ändpunkten för strålarna) kallas för vinkelspets. Normalt markeras en vinkel med en vinkelbåge. Vinkelbegreppet används inom[trigonometri och geometri.

För att mäta vinklar ritas en cirkelbåge med centrum i vinkelspetsen. Radianmåttet för vinkeln är längden av bågen mellan vinkelbenen dividerad med cirkelns radie. Vanligen uttrycks dock vinkeln i grader

[math]\displaystyle{ \theta(rad) = \frac{b{a\!\!^\circ}gl{\ddot a}ngden}{radien} }[/math]

[math]\displaystyle{ \theta(grader) = \frac{b{a\!\!^\circ}gl{\ddot a}ngden}{omkretsen}\cdot 360 }[/math]

Symbolen för enheten grad är en lite upphöjd cirkel (°).

Aktiviteter

Övning: Titta på alla filmer om vinklar på Geogebra

Problemlösning vinklar.

Lär mer

Mycket av informationen ovan kommer från Wikipedia:

• Vinkel