Ekvationer: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) |
||
| Rad 103: | Rad 103: | ||
=== Digitala verktyg === | === Digitala verktyg === | ||
[[Fil:IMG 0795.PNG|höger|GeoGebra CAS]] | [[Fil:IMG 0795.PNG|400px|höger|GeoGebra CAS]] | ||
Versionen från 8 september 2017 kl. 09.04
|
|
Aktivitet
Aktiviteten denna lektion är en tydlig genomgång av hur man löser ekvationer och redovisar sin lösning på ett tydligt kommunicerande sätt.
Dessutom kan vi resonera lite om hur bedömningen ser ut och vilka krav som gäller för olika betyg.
Teori
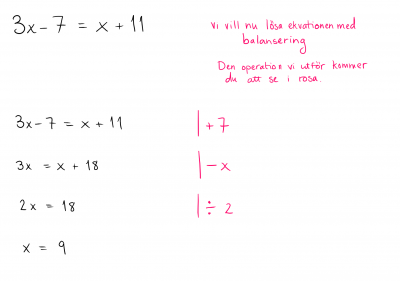
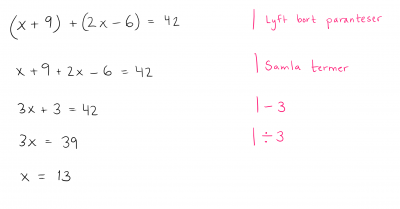
Det är med ekvationer vi beskriver att två matematiska uttryck är lika. Vi skriver ekvationer med hjälp av symboler på var sin sida om ett likhetstecken. Till vänster om likhetstecknet står det vi kallar vänster led, och till höger har vi höger led.
När vi pratar om att lösa en ekvation så är vårt syfte att finna de variabler för vilken likheten stämmer.
Vi kan lösa ekvationer på flera olika sätt.
Ett av de första sättet vi löser ekvationer när vi först stöter på dem i vardagen är oftast identifiering eller prövning. Vid identifiering så försöker vi skriva om ekvationen med enbart tal och ser vilken del som motsvarar vårt x. Och vid prövning så testar vi olika värden för x till dess att vi når en lösning.
Det vanligaste algebraiska lösningssättet är balansering. Den här metoden är den som de flesta har sett någon gång.
Vi vill hålla balansen i ekvationen och allt som görs på den ena sidan likhetstecknet måste även göras på den andra. Så subtraherar vi något från vänster led måste vi även göra det från höger led.
En annan metod vi kan använda oss av är att flytta över hela högerledet så att vårt vänsterled blir lika med 0 (noll) och skriva om vårt uttryck i vänsterled till att endast bestå av produkter och använda oss av något som kallas nollproduktsmetoden. För om en av våra faktorer är noll, så blir produkten noll. På det sättet kan vi få enklare uttryck som är lättare att direkt identifiera. Den här metoden fungerar bra när vi känner oss trygga med faktorisering och att använda oss av kvadrering och konjugering baklänges. Nollproduktsmetoden kommer vi att komma tillbaka till i Ma2c.

Förstå proceduren
Balansering
Genom att behandla båda sidor av ekvationen på samma sätt, balansera ekvationen, kan man skapa nya, enklare ekvationer. Man kan alltid addera, subtrahera, multiplicera eller dividera tal eller uttryck på båda sidor, med bibehållen lösningmängd, undantaget är multiplikation och division med 0.
Genom att multiplicera båda sidor med 1/2 fås:
- [math]\displaystyle{ 1/2 \cdot 2 \cdot x = 1/2 \cdot 3 }[/math] eller
- [math]\displaystyle{ 1 \cdot x = x = 3/2 }[/math].
Det gör att vi nu skrivit om ekvationen på ett sådant sätt att [math]\displaystyle{ x }[/math] måste vara lika med 3/2.
Mer kortfattat kan ovanstående ekvation lösas genom balansering på följande sätt:
- [math]\displaystyle{ 2x+1=4 \quad \Leftrightarrow \quad 2x + \underbrace{1+(-1)}_{=0}= 4 + (-1) \quad \Leftrightarrow \quad 2x = 3 \quad \Leftrightarrow \quad \underbrace{\frac{1}{2} \cdot 2}_{=1} \cdot x \cdot = \frac{1}{2} \cdot 3 \quad \Leftrightarrow \quad x = \frac{3}{2}. }[/math]
Texten ovan från Wikipedia.se
Ekvationer med x i båda leden

Ett exempel på en ekvation med x i båda leden kan vara:
- [math]\displaystyle{ 6 x = 3 x + 2 }[/math]
- [math]\displaystyle{ 3 x = 2 }[/math]
- [math]\displaystyle{ x = \frac{2}{3} }[/math]
Ekvationer med nämnare
På samma sätt som vi kan balansera ekvationer kan vi multiplicera hela ekvationer så att vi får bort oönskade nämnare.
Om ekvationerna innehåller variabler i nämnaren (bråk) måste de förlängas.
Problemlösning med ekvationer
Sammanfattning - Tillämpa proceduren
Det finns fyra procedurer som tillämpas vid ekvationslösning:
- Flytta över termer och byt tecken.
- Flytta upp eller ner till andra sidan.
- Multiplicera allt med minus ett
- Skifta plats på variabel och lösning.
Digitala verktyg
WolframAlpha Alpha.
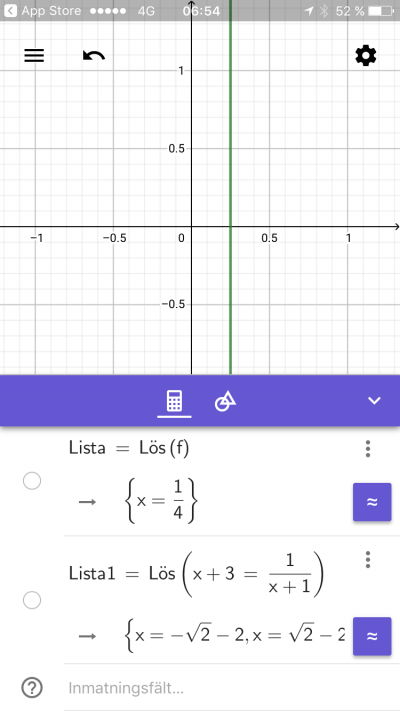
GeoGebra CAS
Öva själv
Ekvationer med x i båda leden
Två-stegs-ekvationer
Testa här om du förstår processen för att lösa två-stegs-ekvationer:
En övning i GeoGebra
Lär mer
Wikipedia skriver om Ekvationslösning#Att_l.C3.B6sa_en_ekvation




