Tal och talmängder: Skillnad mellan sidversioner

Från Wikiskola
Hoppa till navigering Hoppa till sök
VisuellWikitext
Rad 72: Rad 72:
=== Rationella tal ===
=== Rationella tal ===


 
Rationella tal, "bråktal", är de tal som kan skrivas som en kvot (ett bråk) av två heltal:
'''[[Rationella tal]]''', "bråktal", är de tal som kan skrivas som en [[kvot]] (ett [[bråk]]) av två heltal:<ref name="math.se"/>


:<math>\frac{T}{N}</math>
:<math>\frac{T}{N}</math>
Rad 80: Rad 79:


Mängden av de rationella talen betecknas ℚ (eller, av vissa typografiska skäl kan ett vanligt '''Q''' i fetstil används).
Mängden av de rationella talen betecknas ℚ (eller, av vissa typografiska skäl kan ett vanligt '''Q''' i fetstil används).
Ett alternativt sätt att uppfatta denna mängd är som mängden bestående av alla lösningar (''x'')
till [[ekvation]]er {{nowrap|''bx'' - ''a'' {{=}} 0}}, där ''a'' och ''b'' är heltal och ''b'' inte är lika med noll.<ref name = "Rosen">{{Bokref |efternamn = Rosen |förnamn = Kenneth |år = 2007 |titel = Discrete Mathematics and its Applications |upplaga = 6th |utgivare = McGraw-Hill |utgivningsort = New York, NY |isbn = 978-0-07-288008-3 |sid = 105,158-160}}</ref><ref name="Talområden och funktioner"/>
Sedd som en delmängd av de reella talen utgör de rationella talen en [[tät mängd]]; Detta innebär att det alltid finns fler rationella tal mellan två olika rationella tal, och att varje reellt tal kan approximeras godtyckligt väl med ett rationellt tal.
Mängden av de rationella talen är [[uppräknelig]], vilket innebär att det i viss mening finns lika många rationella tal som det finns heltal. Detta kan tyckas vara motsägelsefullt, eftersom mängden av alla heltal är en äkta delmängd av ℚ; Detta följer av den första räkneregeln för bråktal som vi härledde ovan: ''a''/1&nbsp;=&nbsp;''a'' där ''a'' är ett heltal.
Det faktum att man kan koppla samman varje rationellt tal med ett unikt heltal, och vice versa, gör att [[kardinaltal]]et för ℚ är lika med kardinaltalet för ℤ (mängden av alla heltal). På matematiskt språk säger man att det existerar en [[Bijektiv_funktion|bijektiv]] [[avbildning]] mellan mängderna ℚ och ℤ.<ref name="math.se"/>


=== Reella tal ===
=== Reella tal ===

Versionen från 10 augusti 2017 kl. 12.46


Tal

Delmängder till komplexa tal.

Tal är ett matematiskt grundbegrepp som används för att representera olika storheter, det vill säga sådant som går att mäta i bestämda måttenheter, till exempel antal, längd, vikt, volym, temperatur och tryck.<ref name="Matematik minimum - Terminologi">Mall:Webbref</ref>

Ett tal är en abstrakt enhet som representerar ett antal eller ett mått. Inom matematiken är definitionen av tal vidare och inkluderar bland annat naturliga tal, heltal, negativa tal, rationella tal, reella tal och komplexa tal med mera.<ref name="Matematik minimum - Terminologi"/>

Aritmetik, "räknelära", behandlar räknande och innefattar grundläggande egenskaper hos tal, som hur de skrivs och hur de fungerar under addition, subtraktion, multiplikation och division; även andra räkne-operationer som procenträkning, potenser, rotutdragning och logaritmer tillhör aritmetiken.<ref>Mall:Webbref</ref> Algebra kan definieras som en utvidgning av aritmetiken och kan beskrivas som förhållanden, vilka uppkommer, när ett ändligt antal räkneoperationer utförs på en ändlig mängd av tal.<ref>Mall:Webbref</ref>

Tal ska inte förväxlas med siffra eller nummer som har helt andra funktioner. Ibland kallas räkneuppgifter för "tal", då i meningar som Löste du talet?

Typer av tal

Tal brukar delas in i fem grundläggande grupper (mängder):

Grundläggande
[math]\displaystyle{ \mathbb{N} }[/math]
  Naturliga tal  0, 1, 2, 3, 4, … eller 1, 2, 3, 4, …
[math]\displaystyle{ \mathbb{Z} }[/math]
  Heltal  ..., −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, ...
[math]\displaystyle{ \mathbb{Q} }[/math]
  Rationella tal  Mall:Frac där a och b är heltal och b inte är 0
[math]\displaystyle{ \mathbb{R} }[/math]
  Reella tal  Gränsen för en konvergent följd av rationella tal
[math]\displaystyle{ \mathbb{C} }[/math]
  Komplexa tal  a + bi eller a + ib där a och b är reella tal och i är imaginära enheten


De naturliga talen är en delmängd av heltalen det vill säga alla naturliga tal är även heltal, skillnaden i detta fall är dock att heltalen även innefattar negativa tal. Heltalen i sin tur är en delmängd av de rationella talen, de rationella talen är en delmängd av de reella talen, och de reella talen är en delmängd av de komplexa talen.

Naturliga tal

Naturliga tal används för att räkna föremål, till exempel äpplen, så länge de är hela.
Load video
YouTube
Prioriteringsregler

Naturliga tal är de icke-negativa talen {0, 1, 2, 3, …} eller alternativt de positiva talen {1, 2, 3, …}. Den förra definitionen är vanlig i Sverige och allmänt i matematisk logik, mängdlära och beräkningsvetenskap, medan den senare kan hittas i bland annat amerikansk litteratur och bland talteoretiker.

Mängden av de naturliga talen betecknas ℕ (eller, av vissa typografiska skäl kan ett vanligt N i fetstil användas).

Enligt den definition som görs i Matematikterminologi i skolan, utgiven av Statens skolverk i Sverige, ingår talet 0 bland de naturliga talen. Konventionen att räkna 0 bland de naturliga talen förekom inte alls före 1800-talet och tillämpas inte av alla matematiker.

Kul länk: What's special about this number?

Heltal

Heltal innefattar talet noll (0)Mall:Fotnot samt de positiva och negativa talen {…, −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, …}, och är därav unionen av mängden av de naturliga talen.<ref name="Talområden och funktioner"/><ref name="math.se"/>

Mängden av heltalen betecknas ℤ (eller, av vissa typografiska skäl kan ett vanligt Z i fetstil användas), från det tyska ordet Zahlen (som betyder "tal").

Mängden av heltalen är uppräkneligt oändlig.

När det gäller datorsystem används termen heltal (de hela talen) som distinktion till flyttal (de reella talen) eftersom de i datorer hanteras, beräknas och lagras olika.

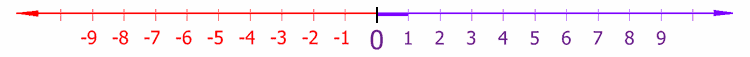
Heltalen kan tänkas vara punkter på en tallinje som sträcker ut sig oändligt långt åt både det positiva och det negativa hållet

Rationella tal

Rationella tal, "bråktal", är de tal som kan skrivas som en kvot (ett bråk) av två heltal:

[math]\displaystyle{ \frac{T}{N} }[/math]

där heltalet T är bråkets täljare och heltalet N bråkets nämnare.

Mängden av de rationella talen betecknas ℚ (eller, av vissa typografiska skäl kan ett vanligt Q i fetstil används).

Reella tal

Reella tal innefattar de tal som man vanligtvis menar med tal. De kan beskrivas som alla punkter på en kontinuerlig linje, utan att det finns glapp mellan talen i linjen. Denna linje brukar kallas den reella tallinjen.

Mängden av de reella talen betecknas ℝ (eller, av vissa typografiska skäl kan ett vanligt R i fetstil användas).<ref>Mall:Webbref</ref><ref>reella tal</ref>

Wikipedia skriver om Tal

Hämtad från ”https://wikiskola.se/index.php?title=Tal_och_talmängder&oldid=40232”