Lektion 7 Cosinussatse: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
||
| Rad 8: | Rad 8: | ||
Nu har du lärt dig de tre triangelsatserna; areasatsen, sinussatsen och cosinussatsen. | Nu har du lärt dig de tre triangelsatserna; areasatsen, sinussatsen och cosinussatsen. | ||
{{clear}} | |||
{{tnkruta | Vilken tycker du är enklast att komma ihåg?}} | {{tnkruta | Vilken tycker du är enklast att komma ihåg?}} | ||
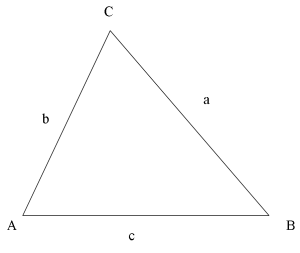
{{defruta | Cosinussatsen | {{defruta | Cosinussatsen | ||
[[Fil:Triangle_ABC_with_Sides_a_b_c.png|300px]] | [[Fil:Triangle_ABC_with_Sides_a_b_c.png|300px]] | ||
Versionen från 9 september 2015 kl. 21.40
Provided ID could not be validated.
Om sinussatsen inte fungerar kan du prova cosinussatsen.
Nu har du lärt dig de tre triangelsatserna; areasatsen, sinussatsen och cosinussatsen.
| Definition |
|---|
| Cosinussatsen |
Härledning

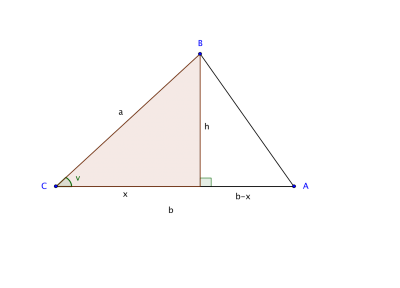
- Rita in en höjd i den vänstra triangeln så att det bildas två trianglar som i den högra bilden ovan.
- Använd Pythagoras för de båda trianglarna
- x2+h2 = a2 (1)
- (x-b)2+h2 = c2
- Förnkla uttrycket ger
- x2+b2-2bx+h2 = c2
- Stuva om i termerna
- x2+h2 = 2bx + c2-b2 (2)
- Sätt x2 + h2 lika. Ekvation (1) i ekvation (2)
- a2 = c2-b2+2bx
- Använd att x = acosC ger
- a2 = c2-b2+2bacosC
- Stuva om så att c2 står fritt ger
- c2 = a2+b2-2abcosC