Lektion 5 - Areasatsen: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) |
||
| Rad 20: | Rad 20: | ||
=== Härledning === | === Härledning === | ||
:[[Fil:Triangle.TrigArea.png]] | |||
Arean av en triangel är lika med basen <math>b</math> multiplicerat med höjden <math>h</math> genom två, det vill säga: | |||
:<math>\ Arean = {b h \over2}</math> | |||
Med hjälp av [[trigonometri]] kan vi teckna följande samband mellan höjden <math>h</math>, sidan <math>a</math> och vinkeln <math>\gamma</math>: | |||
:<math>\sin\gamma = {h \over a}</math> | |||
Vilket är ekvivalent med | |||
: | :<math>\ h = {a \sin\gamma} </math> | ||
Insättning av denna ekvation i den första ger: | |||
:<math>\ Arean = {a b \sin\gamma \over2}</math> | |||
<br /> | <br /> | ||
{{svwp|areasatsen}} | {{svwp|areasatsen}} | ||
Versionen från 7 september 2015 kl. 07.50
Grader och radianer
360 grader motsvarar 2 pi radianer.
Fördjupning: Här finns material att hämta... http://en.wikipedia.org/wiki/Trigonometry
Areasatsen
| Definition |
|---|
| Areasatsen
|
Härledning
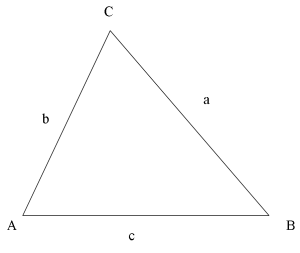
Arean av en triangel är lika med basen [math]\displaystyle{ b }[/math] multiplicerat med höjden [math]\displaystyle{ h }[/math] genom två, det vill säga:
- [math]\displaystyle{ \ Arean = {b h \over2} }[/math]
Med hjälp av trigonometri kan vi teckna följande samband mellan höjden [math]\displaystyle{ h }[/math], sidan [math]\displaystyle{ a }[/math] och vinkeln [math]\displaystyle{ \gamma }[/math]:
- [math]\displaystyle{ \sin\gamma = {h \over a} }[/math]
Vilket är ekvivalent med
- [math]\displaystyle{ \ h = {a \sin\gamma} }[/math]
Insättning av denna ekvation i den första ger:
- [math]\displaystyle{ \ Arean = {a b \sin\gamma \over2} }[/math]