Lektion 5 - Areasatsen: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) |
||
| Rad 13: | Rad 13: | ||
{{#ev:youtube| 3t6AahjyD90 |240|right|Areasatsen, av Mikael Bondestam.}} | {{#ev:youtube| 3t6AahjyD90 |240|right|Areasatsen, av Mikael Bondestam.}} | ||
{{#ev:youtube| DNZ2qja3uO8 |240|right|Areasatsen, av Åke Dahllöf.}} | {{#ev:youtube| DNZ2qja3uO8 |240|right|Areasatsen, av Åke Dahllöf.}} | ||
{{defruta | | {{defruta | '''Areasatsen''' | ||
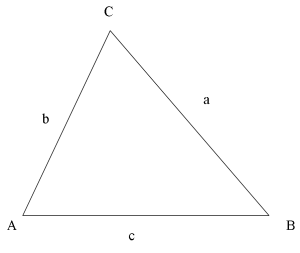
[[Fil:Triangle_ABC_with_Sides_a_b_c.png|300px]] | [[Fil:Triangle_ABC_with_Sides_a_b_c.png|300px]] | ||
<math>\mbox{Area} {{=}} \frac{1}{2}a b\sin C.</math> | <math>\mbox{Area} {{=}} \frac{1}{2}a b\sin C.</math> | ||
Versionen från 7 september 2015 kl. 07.49
Grader och radianer
360 grader motsvarar 2 pi radianer.
Fördjupning: Här finns material att hämta... http://en.wikipedia.org/wiki/Trigonometry
Areasatsen
| Definition |
|---|
| Areasatsen
|
Härledning
Triangeln borde ritas om så att sidan b är bas och horisontell.
Dra en höjd mot triangelns bas (sidan AC i detta fall).
- Höjden h = a sin C
- Triangelns area A = basen * höjden / 2
- Sätt in uttrycket för h ger:
- Arean = 1/2 ab sin C