Kaströrelse: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) (Skapade sidan med ' {{#ev:youtube| KvY8yrbnm50 |320|right}} Se filmen som handlar om bokens sidor 26-33. Det handlar om rörelse i två dimensioner, hur man kan använda koordinatsystem samt de...') |
Hakan (diskussion | bidrag) |
||
| Rad 72: | Rad 72: | ||
Använd ekvationerna för kaströrelsen och bygg en modell av det hela i GeoGebra. | Använd ekvationerna för kaströrelsen och bygg en modell av det hela i GeoGebra. | ||
Bygg en egen simulering av projektilbanor i GeoGebra. Den kan se ut så här ungefär. | Bygg en egen simulering av projektilbanor i GeoGebra. Den kan se ut [https://www.geogebratube.org/material/show/id/150517 så här ungefär]. | ||
<html> | <html> | ||
<iframe scrolling="no" src="https://www.geogebratube.org/material/iframe/id/150517/width/800/height/600/border/888888/rc/false/ai/false/sdz/true/smb/false/stb/false/stbh/true/ld/false/sri/true/at/preferhtml5" width="800px" height="600px" style="border:0px;"> </iframe> | <iframe scrolling="no" src="https://www.geogebratube.org/material/iframe/id/150517/width/800/height/600/border/888888/rc/false/ai/false/sdz/true/smb/false/stb/false/stbh/true/ld/false/sri/true/at/preferhtml5" width="800px" height="600px" style="border:0px;"> </iframe> | ||
</html> | </html> | ||
Versionen från 5 september 2014 kl. 09.26
Se filmen som handlar om bokens sidor 26-33. Det handlar om rörelse i två dimensioner, hur man kan använda koordinatsystem samt det viktigaste i kapitlet - kaströrelse. När du sett filmen svarar du på frågorna nedan. Läs i boken om du vill veta mer. Du kan också titta på teoridelarna nedan.
Frågor
Rörelser kan sammansättas och uppdelas
Rörelser kan studeras i koordinatsystem
Repetition - formler från Fysik 1
Sträcka
s = v0t + at2 / 2
Hastighet
Vid en konstant acceleration a, gäller att:
v = v0 + at
Kaströrelse
Detta avsnitt är hämtat från WikiBooks Formelsamling i Fysik.
|
[math]\displaystyle{ \left\{\begin{matrix} v_x = v_0 \cos \alpha \\ v_y = v_0 \sin \alpha -gt \end{matrix}\right. }[/math] |
|
| [math]\displaystyle{ \left\{\begin{matrix} x = v_0 t \cos \alpha \\ y = v_0 t \sin \alpha -\frac {1}{2}gt^2 \end{matrix}\right. }[/math] | |
| [math]\displaystyle{ h = \frac{v_0^2}{2g}(\sin \alpha)^2 }[/math] |
Kaströrelse i GeoGebra
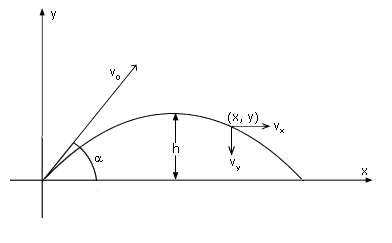
Velocity Components i Projectile Motion
Simulering av kaströrelse
från PhET och Wikipedia: Trajectory_of_a_projectile
Simulera med GeoGebra
Använd ekvationerna för kaströrelsen och bygg en modell av det hela i GeoGebra.
Bygg en egen simulering av projektilbanor i GeoGebra. Den kan se ut så här ungefär.