Versionen från 28 mars 2013 kl. 07.25

Varför ska man lära sig algebra?

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!

Ma2C: Multiplikation, sidan 8-17

Lektion 1

Läs den här: Why Is Algebra Important to learn?

Intro

Kuriosa: Grafer på Google

Algebraintroti boken på sid 3

Gerolamo Cardano funderade över lösingen till följande ekvation

Kan vi dela talet 8 i två delar så att deras produkt blir 25?
x(8-x) = 25

Ekvationen har följande rötter:

x = 4 + rot(-9)
x = 4 - rot(-9)

Ekvationen kan skrivas om på detta sätt:

8x - x² = 25

x² - 8x + 25 = 0

Men vad är roten ur -9? Det är ett imagint tal, som skrivs 3i. Kolla gärna Wolfram Alpha för en lösning till ekvationen ovan

OlleH

öva algebra här: http://olleh.se/start/frageprogramMa2.php

Förenkling av uttryck

Sats: Distributiva lagen

[math]\displaystyle{ a(b+c) = ab + ac }[/math]

Ekvationer

Vid lösning av ekvationer kan du tänka att det är tillåtet att göra samma sak på båda sidor av likhetstecknet. Du kan addera samma sak på båda sidorna. Eller subtrahera samma sak på båda sidorna. På samma sätt kan du multiplicera eller dividera med samma sak på båda sidorna.

Detta kan du använda för att förkorta bort något på ena sidan och resultatet blir att den saken byter upp på andra sidan men med motsatt tecken (plus blir minus osv).

På denna sida från Matteboken.se finns en förklaring skriva om hur man ändrar i ekvationer på detta sätt. Titta gärna på filmen på sidan också.

När man får kläm på det här sättet att ändra i ekvationer brukar man helt enkelt flytta över saker till andra sidan och byta tecken. På så sätt kan man ändra en ekvation så att man får sitt x (eller vilken variabel man nu vill lösa ut) ensamt på en sida.

Kvadrerings- och konjugatregler

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!

Parentesmultiplikation

Multiplikationen är både algebra och geometri

Gånger med bilder from Håkan Elderstig

Hur funkar det om man multiplicerar två parenteser med varandra?

Först inleder vi med ett exempel med siffror

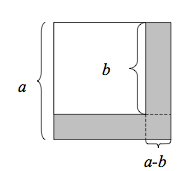
En övning som visar exemplet nedan i bilder. Ett tal kan delas upp i sin entalsdel och sin tiotalsdel innan en multiplikation. PowerPoint. Gånger av tvåsiffriga tal visas med hjälp av bilder. Detta är ett exempel från grundskolan. Det syns till höger.

Exempelvis

[math]\displaystyle{ 12*13=(10+2)*(10+3)=100+30+20+6. }[/math]

Repetition aritmetik: Pappersövning i skriftlig huvudräkning.

Och nu med bokstäver

Tänk sedan att du gör samma sak med bokstäver

[math]\displaystyle{ (a+b)(c+d)=ac+ad+bc+bd }[/math]

<ggb_applet width="796" height="511" version="4.0" ggbBase64="UEsDBBQACAgIAChaLEAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAAoWixAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1b747bNhL/nD4FoQ+HXWxsi9T/nLdFk7uiAZImQHKHw30pKIm2GUuiKlJeb9DHuXuSvtgNScmW7U32T5Oc10E2FMXhDGfmNzMkV5n+sC4LtGKN5KK6dPDYdRCrMpHzan7ptGo2ip0fvv9uOmdiztKGoploSqouHV9T8vzSmSVhMpvFeJRnLBr5LItHSZ6kozwnmEUsSGgWOQitJX9WiV9oyWRNM/YuW7CSvhIZVUbwQqn62WRydXU17kWNRTOfzOfpeC1zB8EyK3npdA/PgN3OpCvPkBPXxZN/vX5l2Y94JRWtMuYgrULLv//uyfSKV7m4Qlc8V4tLJ3Z9By0Yny9Ap9APHTTRRDUYpGaZ4ismYeqga3RWZe0YMlrp8Sf2CRUbdRyU8xXPWXPpuGPiRhHGvk+iOHTDJAwcJBrOKtUR407opGc3XXF2ZfnqJyMSlqmEKFKqWaLff0fEJS56qhtsGwJNGNoh175zPdsQ2/i2CSyNb6f7ltS3NL6l8T0HrbjkacHAw7SQYEJezRpw36Yv1XXBzHq6F1v18VPQSfKPQIxdwIm1uek81T8h/Ph6YLKrJB5IVU17T6G9yCgJ7y6S/ClFvY2aYXQokwSfUDP8jFCr9130xMHAtCDK/DU/BxK9z6m5L9H2bxPoxVpgFPs3Cgz9b6LidNKHyrSLDiQXmrZDj2Kl1PHiJShINOwxCiA2wghQHiCcQBMRBNGAcID8ALo4RqFuI+RFMOAjD8VI02EPmeAIYvjHjwyzEAXATL+NICYRBkE+CjyETUz5CCIJmbiEGCUeUAQBCmCSFo+JZuGFyA+h58XIhzXqkIwwEHowEfogniAPI09PxhEiIQo1P+zrUA9jvXRgSVDoohBrhhDVENE2moE+Rp7Wps9rvKpbtWOirMz7RyXqjS+AGvLRNu3Z/LSTFZ9MC5qyAgrFO+1JhFa00BFhBM1EpVDvRGLfzRtaL3gm3zGlYJZEH+iKvqKKrX8CatnLNrSZqOTbRqgXomjLSiKUicLdrFkUePBMNquGjjcY8IcDwWAgHDxHN8oVMIJayUC+aGRPTvP8pabYpgaw5JuquH7eMLqsBd9VYzoxNWfK2qzgOafVPwGsWoq2C+pLkElXfQnyY69fiGjyd9cSEIzW/2aNgFSFydj3SEKwG/ok9BIHXdsRL/TGQRBjD/s4IJHnQYmRGdWxFwXjIIxiQlwvCeMw0ZO6oZCMcRyGOHSjIPEJDgIrmq02HqJrtlV23ph6v+28lM9FsX1l9H9Ba9U2ZvcAybHRWv1YzQtmMGIiG0pztkzF+p0Fh2d5vb+uoefaFaRzY3cEuYHoAj3v2hTafpV6aRsq19C4hsLt0cbzzThOiKEwbWpbQwXwtUvrVMW9mtjtxXBpMprrdHHTZysNfl3p24qrV31H8Wy5VVVP+KUtU7aB0C5P/KV4Tid7GJsuWVOxooM0OLMVrbQROkB7zjJeQtcOdCah2l3/gAXYtzmbN6xfeGF2ZtZgZtQdovXgtWH1UyPKl9XqPWBhbwHTSb/KqcwaXmvMoRTKwJJtUZVzSaGK5MN5OgZB9UxXCzCP0qY5oxfp+Vl2kZ9DnLZqIcDtP//x3yWt0N8L2IlJxefADdIN2NRsBEWzlAvG1Hu2VoimYgUjr9tC8brgS1OJEF0h2ZYlgIhXokQ1bWDbxiRr0B//aWCjDK9VI/J22a2kKNByRfOG6QiQDQP1m4oikS3QUlQf2jlV8JIV1RhgyArteqMQK1gJnJEyUVC1JTDINnjIfiVmxWC9tjMwGYfWxBoOSKQfIC1vKredtcUbDH8iUhAt6gXVm1TcxQO9BuWGPjTcXou8E9zRyULvblHJK8OmpGuoz8AulZCwFWzvATPVdntvF9YlPNga6cMDzPBD/XANqQIH+mnG12xTjsCD/CNgl+7osg1YBbVkCRtmaTZxqssf5uFnnues2iyWVoBy4yFIp7XVFkElYzYEN1Nr0N5krgFCO8/c6qP00Ed47J+Cj+LORyR8BD5a1w1I02w6C/8NzrNr4HfmPkXgo/OelSlWdp+z69huYDP9wIG7ufpmD2IS2Hqj265qbf3o3tGPw+QqtS/czhUaWeijPa7b86petC6oO5sw+3YvK98d0vRkIR31kMb+I4T08x7S4KCnyL0vpJ8fFaQNlK87aH8JSB+Y68WOuR6QA148zGBDyH9hY32d+N/V+sf/s9Z3ih58U/TclDG/FLwyUZa0ylFlLjLeiuJ6Lipne7SmrrYcotiEKSUGftTThcSaqlU9GU0tHbV0aWoJs19BKQpH19TK7iTe4C0re5OtU+ehieq+yRwHnvFygB+cz2+BomRz3dsqdwjGP7fOL1aCt6weYHj2W2WnSHu84yUcPTKuNlgpNLRfwpGjkcycdg7PcEvGan14flO9b2gl9f28pRmcDe9o5TS9xcwDsV/bzqPDwpAEyfBPdDJ21yF/NIbvAT7aFpmTNfxteP92aWUf7Y8rrdylKj631e6MoguU9RtXXfi2b9JzWwLPqHneL5hpZllkdh6zxDNbLef3q5bA63SrZXY0sO6Tib6uenyw/ryV2fHk7INiGfTXgydg59nx2HlTG3s8e+PQO9HaOD8es++je3RCW5L9S7e82wvuXLp53/LS7c1sJpnSdje/YdQXbF//Rq6/ZPZCcvQ3cnfZ7Zjr5vN+y9M9k+4Z9jvg5n6z4w7eHNwR5JbFws7mdsoHu+XJ73lBkJ/wlmdxPNlq/4bglLLVvtn58ZgdzOy5O3+8vfuD+OB3/o/W7h+Ox+4H9wXeOIpPxtD50RylboH34zpZ3amE0mEJ1XcEwzLa9XdLKf1MKc26UlpYDqWdUtlSWt+vlGanXEqL48st/XFrdMLnrfJ4zH5bKQ3GZGcUn4wTquNxwsFdQzR2yWlavT4eq9+C/NFj20UefA2hP3bE3RcRf/mtFeqvZ+lFfn5GL7JzdAnn9os0u6D5RZbbUcNx130KWDi7/B7kv09dT9zTeeZTc8kaPtt+lt39nwynN3RHKhVt1Fv9O35k8hzIcv2YRG4SxYHv4iDRc+xmliS+G2E3ICQK/QgPvx4YWngy/BbVfPLd/fel7/8HUEsHCKNA+swOCQAAWzUAAFBLAQIUABQACAgIAChaLEBFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgAKFosQKNA+swOCQAAWzUAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACmCQAAAAA=" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> Hela filen kan laddas ner här.

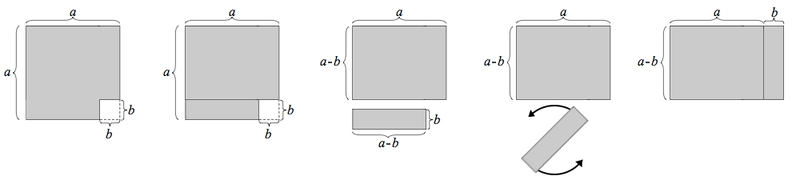
Bevis som utgår från distributiva lagen

[math]\displaystyle{ x(c+d) = xc+xd }[/math]

Antag att [math]\displaystyle{ x = a+b }[/math] och sätt in i uttrycket ovan.

[math]\displaystyle{ (a+b) c+(a+b)d }[/math]

[math]\displaystyle{ c(a+b)+d(a+b) }[/math]

[math]\displaystyle{ ca+cb+da+db }[/math]

[math]\displaystyle{ ac+bc+ad+bd }[/math] V.S.B.

Läs om distributiva lagen på wwebbmatte.

Öva på Khan: Hitta faktorerna till ett uttryck:

solving quadratics by factoring

Öva hos OlleH: http://olleh.se/start/frageprogramMa3.php

Kvadreringsregeln

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!

Lektion 2

Mål för undervisningen Du ska lära dig kvadreringsreglerna. Det är mycket viktigt.

Första och andra kvadreringsreglerna

Kvadreringsreglerna är regler i algebran om hur man utvecklar uttrycken

[math]\displaystyle{ \ (a+b)^2=a^2+2ab+b^2 }[/math]	(Första kvadreringsregeln)
[math]\displaystyle{ \ (a-b)^2=a^2-2ab+b^2 }[/math]	(Andra kvadreringsregeln)

Texten i ovanstående avsnitt kommer från Wikipedia.se

Förklaring

(a-b)² =  
(a-b)(a-b) =
a²-ab-ba+b² =          ( och ab = ba )
a²-2ab+b²                V.S.B.

Länkar:

Bondestam respektive Wille på Mattecentrum om kvadreringsregeln:

Potenslagarna, av Åke Dahllöfr

WolframAlpha Widget

Här kan du testa att låta datorn göra parentesmultiplikation:

En första läxa

Det är viktigt att vi kommer igång med att lära oss Geogebra.

Första naturliga ingången är egentligen räta linjen där det blir en tydlig koppling mellan funktion och utseende.

GGB-uppgift 1

Ladda ner programmet.

Skriv in en valfri räta linjens funktion.

Ändra färg och tjocklek på grafen.

Ändra så att grafens egenskap syns.

Mejla filen till din lärare.

Konjugatregeln

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!

Lektion 3

Mål för undervisningen Du ska lära dig konjugatregeln. Det är mycket viktigt.

Konjugatregeln

Ma2C: Konjugatregeln, sidan 22-24

Så här ser den ut:

a²-b² = (a-b)(a+b)

[math]\displaystyle{ (a-b)\cdot(a+b) }[/math]

[math]\displaystyle{ = a^2 +a\cdot b -a\cdot b -b^2 }[/math]

vi kan stryka ab - ba = ab - ab = 0:

[math]\displaystyle{ = a^2-b^2 }[/math]

V.S.B.

Film

Bondestam (tv) respektive Matteboken (th) förklarar:

Geometriskt bevis av konjugatregeln

Första beviset

Andra beviset

Visualisering

  Här gäller:

  [math]\displaystyle{ (x-y)\cdot(x+y) = x^2 - y^2  }[/math]

  Denna är gjord med Geogebra, sparad som animerad gif, upladdad till WIKIMEDIA COMMONS och länkad hit.

  [math]\displaystyle{ (a - b)\cdot(a + b) = a^2 - b^2  }[/math]

Länk till filen

Uppgifter

Övningar (utan räknare)

  1. [math]\displaystyle{ 1992\cdot 2008 = ? }[/math]

  2.  Lös  [math]\displaystyle{ x^2-1=0 }[/math] för alla reella x.

  Tips : Använd konjugatregeln och nollregeln för ekvationen.

Öva på Khan: Khan: Parentesmultiplikation

Hunnet så här långt kan vi repetera genom att lösa lite uppgifter på Khan Academy. De är dels av typen (a+b)(c+d) men också sådana som tillämpar kvadreringsregeln.

Khan om hur man multiplicerar binom ska du verkligen öva på.

Webbmatte

Konjugatregeln på Webbmatte

Uppgift

Diagnos 11

Rättelse: I lösningen till uppgift 6 finns tyvärr inte med att lösningen även har en negativ rot. Detta kommer vi att gå in noggrannare på i avsnitt 1.3 som behandlar andragradsekvationer.

Snabbdiagnos 1

Du kan printa denna! snabbdiagnos1 kvadrerings- och konjugatreglerna

Ekvationer med x²-term

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!

Ma2C: Ekvationer, sidan 25-29

Lektion 4

Repetition

Gör Khan-uppgiften från förra avsnittet om du inte redan gjort det.

Intro

Detta avsnitt handlar om ingenting kan man säga. Det handlar nämligen om ekvationer med x²-termer som försvinner vid förenklingen.

Räkna uppgifterna: 1245-1258

Läxa! Gör dessa uppgifter i GeoGebra

Uppgift 1251: Här gör du skissen i GeoGebra.
Uppgift 1257: Läs om en Ellips på Wikipedia.
- Pröva att göra en ellips i GeoGebra. Ledining skriv in ekvationen (x/a)^2+(y/b)^2=1. Välj själv värden på a och b.
- Sök på Ellipse på GeoGebraTube.org. Inte ett facit till ellipsen.
- Titta på en ellips i Wolfram

En laborativ datorövning på pascals triangel

Aktivitet

Ta ett papper och en penna och utför följande:

Utveckla [math]\displaystyle{ (x+y)^2 }[/math]
Utför nu [math]\displaystyle{ (x+y)(x+y)^2 }[/math]
Summera de termer som är lika.
Nästa steg blir förstås [math]\displaystyle{ (x+y)(x+y)^3 }[/math]
Studera polynomen ovan genom att skriva dem under varandra. Vad ser du för mönster gällande antalet termer och gradtalen för termerna
Läs på om Pascals triangel och skriv polynomet för [math]\displaystyle{ (x+y)^4 }[/math] och [math]\displaystyle{ (x+y)^5 }[/math]
Skriv en förklaring med egna ord hur Pascals triangel hänger ihop med koefficienterna till polynomen av [math]\displaystyle{ (x+y)^n }[/math]
Hur ser polynomet för [math]\displaystyle{ (x+y)^{11} }[/math] ut?
Hur ser polynomen för [math]\displaystyle{ (x-y)^2 }[/math], [math]\displaystyle{ (x-y)^3 }[/math], ... ut?

Lär mer

Wikipedia Pascals triangel

En triangel som är förvånansvärt mångsidig - NCM

Okända skrymslen i Pascals triangel - NCM

Andragradsekvationer

Enkla andragradsekvationer

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!

Ma2C: pq-formeln, sidan 30-32 och 35-38

Lektion 5

Av Daniel Barker.

Den här behöver man fundera på en stund. Quadratic equations in early Baghdad

Även nu har vi att göra med andragradsekvationer som är enkla fall av den fullständiga ekvationen.

Antingen förkortas x-termerna bort så att man får kvadrattermer kvar att ta roten ur

eller

så har man ett kvadraten på ett binom (ett parentesuttryck upphöjt till två) som man tar roten ur.

I båda fallen blir det en positiv och en negativ rot som svar (eller cdel av svaret men det blir inga imaginära tal eller komplexa rötter i detta avsnitt.

Fullständiga andragradsekvationer

pq-formeln - Förklaring

Mål för undervisningen Du ska lära dig pq-formeln. Det är mycket viktigt.

En generell beskrivning av en andragradsekvation ser ut så här:

[math]\displaystyle{ x^2 + px + q = 0 }[/math]

där p och q är tal (siffror) i den speciella ekvationen.

Den allmänna ekvationen har lösningen:

[math]\displaystyle{ x=-p/2 \pm \sqrt{(p/2)^2-q} }[/math]

Om du vill lösa en ekvation behöver du bara ta reda på vad p och q motsvaras av i din ekvation och sedan sätter du in dessa siffror i formeln ovan.

Tänk på att det inte ska stå någor framför [math]\displaystyle{ x^2 }[/math]-termen

Flipp: Se två filmer med Michael Bondestam:

Räkna själv

Lösning: 1339 har jag gjort i ggb och den finns på hårddisken.

Mario om nytan med andragradsekvationer:

Kvadratkomplettering

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!

Ma2C: Kvadratkomplettering, sidan 33-34

Lektion 6

Man kan börja med kvadratkomplettering som en inledande förklaring till pq-formeln men det är lika bra att ge sig på pq-formeln direkt. Sedan kan man gå tillbaks till kvadratkompletteringen för att få ett bevis för att pq-formeln fungerar.

Uppgift:

Öva på Khan: Solving Quadratics by facoring

Lös dessa Khan, relativt enkla andragradsekvationer. De kan lösas genom att gissa eller faktorisera.

Möjligen kan det vara svårt att veta hur de menar att man ska göra på vissa uppgifter. Ta reda på rötterna och faktorisera så går et bra.

Diagnos 2 med pq-formeln

Du kan printa denna! Snabbdiagnos 2

Andragradsekvationer och rötter

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!

Ma2C: Diverse, sidan 39-44

Lektion 7

Exempel

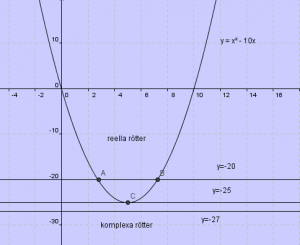
Lös ekvationen:

[math]\displaystyle{ x^2-8x+16=0 }[/math]

Vad händer?

Pröva nu ekvationen:

[math]\displaystyle{ x^2-8x+17=0 }[/math]

här har vi en ekvation som saknar reella lösningar.

Definition
En andragradsekvation kan ha två reella rötter eller en dubbelrot eller två komplexa rötter

<ggb_applet width="809" height="321" version="4.2" ggbBase64="UEsDBBQACAAIANRwPUIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIANRwPUIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7VhZb9tGEH5OfsWAT0lrU7vLO5ASJAGKpnCCoE6Log8FVuRK2pgiCR6SHOTHd2aXpCg7DuI4fattaQ/OzrXfHPT8xWGbw07VjS6LhcNd5oAq0jLTxXrhdO3qPHZePH88X6tyrZa1hFVZb2W7cHxXOMdzuHJ5TId1tnAkX8YqC/h5wMXq3Jc8PU9SEZ7L5UpJLleeyAIH4NDoZ0X5Tm5VU8lUXaYbtZUXZSpbw3PTttWz2Wy/37uDdLes17P1eukemswB1LxoFk4/eYbsTg7tPUMuGOOzv95eWPbnumhaWaTKAbKq088fP5rvdZGVe9jrrN0snFigGRul1xsy08PFjIgqtLVSaat3qsGjk6Wxud1WjiGTBT1/ZGeQj+Y4kOmdzlS9cJgrfC9h0y8Hylqrou2JuRV6iwk/5RIm6GE+ft3BZT4blJrvtNpb7WhmFPdZEuFN6kYvc7VwVjJv0Dm6WNV4MWhX3eGyaa9ztZT1sJ5odIa/SKA/KeKF3rLeXDgi8s/i8Cxi7CwI2GDQKJdPhFqmo8xeh6PQfuNE6iDTiyYyOQqjT4gfo8wNoeihtixzw5RBkMDnzyCYYHBGA7eDwCEM7SNm95hnB2EH3w6BpfHtcd+S+pbGtzS+9xXf3s9Odg8744mdnIz4DJy0N4MHpDc3+tPg98vQLiMzcGYH3j+M6cv4K3ygRd53WcTDe+DlNkhHoULwo9AAoUl/5nNLpHgIQo8Cv2SlCL5spSfu49xbZg4yecC+1cjQf0jwf4dACtf/XuB8NqS6eR8I0GyItr/IVm0bSgFeYrIAcAgwSsIIgzYAnuAQUbQI4AH4AS55DCGNEXgUID54EAPRcQ9MrAcxfvkmeEIIkBdtRjaKwPMh8ICbDOED5gUwWQYzjvCQIgggwEMknZNYLwQ/xIUXg48KUn6JKIY9PIdrFC7A4+DRWR6BCCEUEFGO4j6lrjAm3ZGpgJBBSEcxSWGCsskJT8TgkTUYVFXZ6NG5G5VX460YP+qi6toT36XbbJi25Q3qrEyvXt3wtZJNO8yRCKvRsXTa6nRSWR/Nc7lUOfYflwQDgJ3MKZwM/1VZtDBAQNi9dS2rjU6bS9W2eKqBj3InL2SrDr8gdTMoaESbgj9XXZrrTMviT8QIsSCGMNR/U1CG+u8xbqWkZVlnl9cNAgcOf6u6pGDmrheLiIfMT3ASYlNzbR8JEbjcSxIeYYn2IwrrJpWEeO65fsIiKjqJH0Yex/i77p+FLnYCYcK9IKZJEFvRajeaJg+qGXy5rimceu/T4k3zqsyPW1Wpi/a1rNquNs0cZqSajHpZrHNlfGuuHNui9GpZHi6tUz3L68N1hStmFViuX5d5WQMGpAjQyHU/Lu1oaEizkYoZGmYo2HBLOhuf80QYCjMu7Wio8Nqtar2lfDCTs0GMbkwaQeZTkBnMUJPVFbq9GBatTq+OlhL9u267RLj1x05Z8h/Ecj67AbDbgKPkZM+BmRJkrDYnUDTFaoAi9lN3QzFIXDb5ESMS/cB3k+mPP0IxYCdnWDiB4s1n3L8DixP8/Q/GsQ34kWh8KM/bcLxSdaFyC6UCL7Mru8am2TFVPpp3jXov283LIvtdrbE+vJdUoltkbUmPKmcq1Vs8aPd750m62D9QVbubqXWtBhNz8zJnXWuesimwb20bVr/U5fZNsfuAqLmh6nw22DNv0lpXhE5YYs9wpY74y3QjsePIpufQ+AatSKn6oSNbcqIDsms3ZW3e17CGoD0J/CaLTtYayzYiksI5V1t8y4LW4LLotqrW6XhD0rwHoo5dbwaP3N4Suh8olx+x2N3IMn2p3I2VDqnuQDDIvNpIev/rS1MurymPTDxmmL4ts0GBXnpOL46w1YWBMGzlgdpTZ8g2Pr2/49a557KTlJFgm3CNnZsbnOxi0K30QY3dALpNf0JAnaLjGEUtVukrfBFtTGvd9kFtJr/qLFPFqKksEFDmWjDJVRbalVI2KsaDFRpukskECv3V0CUdqhplEZPexyt08IEalieHp7CAwz9PxFM4xzbuJzjAzyBte3J6uauuMPhwjky+fpGTCPqWK2TfeIXse505dclsinjTDvX/V3n+L1BLBwhQu8auIgYAAAcSAABQSwECFAAUAAgACADUcD1C1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIANRwPUJQu8auIgYAAAcSAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAuQYAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />

Uppgift
Lös uppgifterna i denna gamla Diagnos 12 Genomgång av diagnosen: Facit till Diagnos 12

Komplexa tal

Teori

Definition

Komplexa tal

[math]\displaystyle{ \sqrt{-1} = i }[/math]

[math]\displaystyle{ i^2 = -1 }[/math]

Ett komplext tal består av en realdel [math]\displaystyle{ a }[/math] och en imaginärdel [math]\displaystyle{ b }[/math].

[math]\displaystyle{ z = a + bi }[/math]

Läs mer: Komplexa tal på wikipedia

Vad ska man ha komplexa tal till?

komplexa tal

Komplexa tal används när man räknar på växelström.
- Titta på denna ppt från Uppsala.
- j-omegametoden

Komplexa rötter

x² = -16 har ingen reell rot men däremot två komplexa. Det beror på att lösningen är roten ut ett negativt tal. Roten ur -16 är +4i respektive -4i.

x²+3x+16=0 har också två komplexa rötter fast här beror varje rot av både en realdel och en imaginärdel.

Rotekvationer

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!

Ma2C: Diverse, sidan 45-49

Lektion 8

Rotekvationen

Teori

Rotekvationer innehåller x-termer och roten ur x-termer. Man löser dem genom att kvadrera båda leden.

[math]\displaystyle{ \sqrt{x+2} = x }[/math]

Kvadrera båda sidorna:

[math]\displaystyle{ x+2 = x^2 }[/math]

[math]\displaystyle{ x^2 - x - 2 = 0 }[/math]

[math]\displaystyle{ x = \frac{1}{2} \pm \sqrt{\frac{1}{4} + 2} }[/math]

[math]\displaystyle{ x = \frac{1}{2} \pm \sqrt{\frac{1}{4} + \frac{8}{4}} }[/math]

[math]\displaystyle{ x = \frac{1}{2} \pm \sqrt{\frac{9}{4}} }[/math]

[math]\displaystyle{ x = \frac{1}{2} \pm \frac{3}{2} }[/math]

[math]\displaystyle{ x_1 = - 1, x_2 = 2 }[/math]

Viktigt att kolla om man har falska rötter.

[math]\displaystyle{ -1 }[/math] är en falsk rot eftersom den inte gör att vänster led och höger led blir lika i ursprungsekvationen.

Svaret är alltså [math]\displaystyle{ x = 2 }[/math]

Problemlösning med ekvationer

Professionell matte

Har ni tänkt på att det är ett tag sedan vi gjorde matte som man har nytta av i vardagen? Kvadreingsregeln, konjugatregeln, kvadratkompletteringen och pq-formel hör inte till vardagsmatten. De hör till den professionella matten. Sådan matte som ingenjörer använder.

Vad ska man ha andragradsekvationer till?

De används i spel till exempel.

Wikipedia om projectile motion
Här finns länkar om fysikmotorn bakom Angry Birds och mycket annat
Det finns ett exempel med två bollar som faller och där den ena även far i x-led. Banan beskriver en parabel och det är ett klassiskt exempel på en andragradsekvation. Du kan se Action Script-koden.

PhET

En idé kan vara att ta en screenshot på en projektilbana från PhET-simuleringen ovan och klistra in i GeoGebra. Sedan sätter man tre eller fler punkter på kurvan och anpassar till en andragradsekvation. Det visar om inte annat bakvägen att fysiken innehåller andragradsfunktioner. Om man är osäker på hur man anpassar punkter till en funktion så har jag gjort det med mätvärdena från laborationen på tyngdacceleration.

Ekvationslösning med faktorisering

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!

Ma2C: Faktorisering, sidan 50-56

Lektion 9-10

Diagnosen blir läxa att göra om hemma och denna gång ska den ha alla rätt. Det gäller alla. Facit kommer upp på tisdag så kan alla rätta själva.

Facit till Diagnos 13

På tisdag som är en lång lektion kommer vi att göra uppdelning i faktorer både med konjugatregeln och kvadreringsreglerna om det går.

Uppdelning i faktorer med konjugatregeln

Uppgift
Först ska vi repetera konjugatregeln med ett lösblad där det är rad snabba uppgifter. Dessa uppgifter bör klaras av på mindre än tre minuter.

Uppdelning i faktorer med kvadreringsreglerna

Uppgift
Här ska vi också repetera kvadreringsreglerna med ett lösblad.

Faktorisering och ekvationer

Onsdag

Repetera lösbladet från förra lektionen en gång till. I övrigt struntar vi i beting på faktorisering med kvadreringsregelerna.

Dagens beting: 1426-1430

Dataövning - konsekutiva tal

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!

Ma2C: Konsekutiva tal, sidan 57

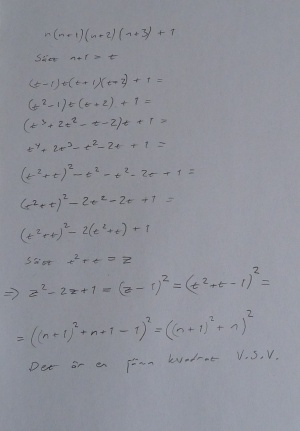
Del ett (n-1)(n+1)+1

Del två

Del tv är svårare. Det handlar om fyra konsekutiva tal. Addera ett till produkten av de fyra talen och ta roten ur. Detta ska bli ett heltal.

Wolfram|Alpha har en lösning men ingen förklaring.
Med hjälp av den ledtråden från Wolfram ser min lösning ut så här.
Tanja löser uppgiften genom att pröva.
Fredrik använder kvadratkomplettering och substitution för att lösa uppgiften. Lösningen syns i bilden till höger.
Charlie i NV11 löser det genom att hitta mönster i de tal han prövar med och ...

Prov onsdag vecka 6

Lektion 11-12

Uppgift
Diagnos 14 Diagnos 14 Diagnos 14 Facit

Repetition på fredag och måndag

Uppgift: Khan Academy

Öva på Khan:

Khan om hur man multiplicerar binom ska du verkligen öva på.

Uppgifter

Läs sammanfattningen på sidan 54.
Gör Test 1 på sidan 55.

pappersövningar

Öva ekvationer (= Extrablad ekvationer): finns bara på papper
Faktorisering: finns bara på papper
Öva enkla andragradsekvationer: finns bara på papper

Du kan printa denna!

Nöt in detta som du måste kunna!

Provet skall vara tisdag vecka 7 (ligger på SchoolSoft).

@@ Rad 1: / Rad 1: @@
+== Varför ska man lära sig algebra? ==
-Kapitel 1 i boken Matematik 2C innehåller 16 delar vilket rimligen bör ta omkring 16 lektionstillfällen eller fyra veckor i anspråk.
+{{flipp| - }}{{lm2c|Multiplikation|8-17}}  {{TE12A|1}}
-[[File:Binomio al cubo.svg|right|400px|Binomio al cubo]]
-= Repetition =
-Varför ska man lära sig algebra?
 <youtube>Cq832vvq9PE</youtube>
+'''Läs den här:''' [http://www.garnermath.com/downloads/Usiskin_Why-is-Algebra-Important.pdf Why Is Algebra Important to learn?]
-== Mål för wikiskola på denna sida ==
-Ett mål för denna kurs är att varje avsnitt om möjligt ska ha ett videoklipp med någon som förklarar, relevant länk till Khan samt en GGB el dyl som anknyter till bokens teoridel. Dessutom vore det fint med några egna övningsuppgifter och någon datorövning.
 == Intro ==
@@ Rad 36: / Rad 29: @@
 Men vad är roten ur -9? Det är ett imagint tal, som skrivs 3i. Kolla gärna Wolfram Alpha för en [http://www.wolframalpha.com/input/?i=x%288-x%29%20%3D%2025&t=ff3tb01 lösning] till ekvationen ovan
+'''OlleH'''
+öva algebra här: http://olleh.se/start/frageprogramMa2.php
 == Förenkling av uttryck ==
@@ Rad 41: / Rad 38: @@
 '''Sats: Distributiva lagen'''
- a(b+c) = ab + ac
+:<math> a(b+c) = ab + ac</math>
 == Ekvationer ==
@@ Rad 54: / Rad 51: @@
 = Kvadrerings- och konjugatregler =
+{{flipp|-}}
 == Parentesmultiplikation ==
@@ Rad 69: / Rad 66: @@
 En övning som visar exemplet nedan i bilder. Ett tal kan delas upp i sin entalsdel och sin tiotalsdel innan en multiplikation. <font color=darkgreen>PowerPoint</font color=darkgreen>. [[Media:Ganger_med_bilder.ppt|Gånger av tvåsiffriga tal ]]visas med hjälp av bilder. ''Detta är [[Övningar_tal_och_räkning_6B|ett exempel från grundskolan]].'' Det syns till höger.
-  exempelvis
+'''Exempelvis'''
-*13=(10+2)*(10+3)=100+30+20+6.
+: <math> 12*13=(10+2)*(10+3)=100+30+20+6.  </math>
+<br />
 '''Repetition aritmetik:''' Pappersövning i [[Media:Skriftlig_huvudrakning_ovning.doc|skriftlig huvudräkning]].
@@ Rad 76: / Rad 75: @@
 === Och nu med bokstäver ===
+{{#ev:youtube| HPAorEQ3gm4|240|right}}
 [[Fil:Abcd.png|thumb|(a+b)(c+d)=ac+ad+bc+bd]]
 Tänk sedan att du gör samma sak med bokstäver
- (a+b)(c+d)=ac+ad+bc+bd
+: <math> (a+b)(c+d)=ac+ad+bc+bd</math>
 <br>
 <ggb_applet width="796" height="511"  version="4.0" ggbBase64="UEsDBBQACAgIAChaLEAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAAoWixAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1b747bNhL/nD4FoQ+HXWxsi9T/nLdFk7uiAZImQHKHw30pKIm2GUuiKlJeb9DHuXuSvtgNScmW7U32T5Oc10E2FMXhDGfmNzMkV5n+sC4LtGKN5KK6dPDYdRCrMpHzan7ptGo2ip0fvv9uOmdiztKGoploSqouHV9T8vzSmSVhMpvFeJRnLBr5LItHSZ6kozwnmEUsSGgWOQitJX9WiV9oyWRNM/YuW7CSvhIZVUbwQqn62WRydXU17kWNRTOfzOfpeC1zB8EyK3npdA/PgN3OpCvPkBPXxZN/vX5l2Y94JRWtMuYgrULLv//uyfSKV7m4Qlc8V4tLJ3Z9By0Yny9Ap9APHTTRRDUYpGaZ4ismYeqga3RWZe0YMlrp8Sf2CRUbdRyU8xXPWXPpuGPiRhHGvk+iOHTDJAwcJBrOKtUR407opGc3XXF2ZfnqJyMSlqmEKFKqWaLff0fEJS56qhtsGwJNGNoh175zPdsQ2/i2CSyNb6f7ltS3NL6l8T0HrbjkacHAw7SQYEJezRpw36Yv1XXBzHq6F1v18VPQSfKPQIxdwIm1uek81T8h/Ph6YLKrJB5IVU17T6G9yCgJ7y6S/ClFvY2aYXQokwSfUDP8jFCr9130xMHAtCDK/DU/BxK9z6m5L9H2bxPoxVpgFPs3Cgz9b6LidNKHyrSLDiQXmrZDj2Kl1PHiJShINOwxCiA2wghQHiCcQBMRBNGAcID8ALo4RqFuI+RFMOAjD8VI02EPmeAIYvjHjwyzEAXATL+NICYRBkE+CjyETUz5CCIJmbiEGCUeUAQBCmCSFo+JZuGFyA+h58XIhzXqkIwwEHowEfogniAPI09PxhEiIQo1P+zrUA9jvXRgSVDoohBrhhDVENE2moE+Rp7Wps9rvKpbtWOirMz7RyXqjS+AGvLRNu3Z/LSTFZ9MC5qyAgrFO+1JhFa00BFhBM1EpVDvRGLfzRtaL3gm3zGlYJZEH+iKvqKKrX8CatnLNrSZqOTbRqgXomjLSiKUicLdrFkUePBMNquGjjcY8IcDwWAgHDxHN8oVMIJayUC+aGRPTvP8pabYpgaw5JuquH7eMLqsBd9VYzoxNWfK2qzgOafVPwGsWoq2C+pLkElXfQnyY69fiGjyd9cSEIzW/2aNgFSFydj3SEKwG/ok9BIHXdsRL/TGQRBjD/s4IJHnQYmRGdWxFwXjIIxiQlwvCeMw0ZO6oZCMcRyGOHSjIPEJDgIrmq02HqJrtlV23ph6v+28lM9FsX1l9H9Ba9U2ZvcAybHRWv1YzQtmMGIiG0pztkzF+p0Fh2d5vb+uoefaFaRzY3cEuYHoAj3v2hTafpV6aRsq19C4hsLt0cbzzThOiKEwbWpbQwXwtUvrVMW9mtjtxXBpMprrdHHTZysNfl3p24qrV31H8Wy5VVVP+KUtU7aB0C5P/KV4Tid7GJsuWVOxooM0OLMVrbQROkB7zjJeQtcOdCah2l3/gAXYtzmbN6xfeGF2ZtZgZtQdovXgtWH1UyPKl9XqPWBhbwHTSb/KqcwaXmvMoRTKwJJtUZVzSaGK5MN5OgZB9UxXCzCP0qY5oxfp+Vl2kZ9DnLZqIcDtP//x3yWt0N8L2IlJxefADdIN2NRsBEWzlAvG1Hu2VoimYgUjr9tC8brgS1OJEF0h2ZYlgIhXokQ1bWDbxiRr0B//aWCjDK9VI/J22a2kKNByRfOG6QiQDQP1m4oikS3QUlQf2jlV8JIV1RhgyArteqMQK1gJnJEyUVC1JTDINnjIfiVmxWC9tjMwGYfWxBoOSKQfIC1vKredtcUbDH8iUhAt6gXVm1TcxQO9BuWGPjTcXou8E9zRyULvblHJK8OmpGuoz8AulZCwFWzvATPVdntvF9YlPNga6cMDzPBD/XANqQIH+mnG12xTjsCD/CNgl+7osg1YBbVkCRtmaTZxqssf5uFnnues2iyWVoBy4yFIp7XVFkElYzYEN1Nr0N5krgFCO8/c6qP00Ed47J+Cj+LORyR8BD5a1w1I02w6C/8NzrNr4HfmPkXgo/OelSlWdp+z69huYDP9wIG7ufpmD2IS2Hqj265qbf3o3tGPw+QqtS/czhUaWeijPa7b86petC6oO5sw+3YvK98d0vRkIR31kMb+I4T08x7S4KCnyL0vpJ8fFaQNlK87aH8JSB+Y68WOuR6QA148zGBDyH9hY32d+N/V+sf/s9Z3ih58U/TclDG/FLwyUZa0ylFlLjLeiuJ6Lipne7SmrrYcotiEKSUGftTThcSaqlU9GU0tHbV0aWoJs19BKQpH19TK7iTe4C0re5OtU+ehieq+yRwHnvFygB+cz2+BomRz3dsqdwjGP7fOL1aCt6weYHj2W2WnSHu84yUcPTKuNlgpNLRfwpGjkcycdg7PcEvGan14flO9b2gl9f28pRmcDe9o5TS9xcwDsV/bzqPDwpAEyfBPdDJ21yF/NIbvAT7aFpmTNfxteP92aWUf7Y8rrdylKj631e6MoguU9RtXXfi2b9JzWwLPqHneL5hpZllkdh6zxDNbLef3q5bA63SrZXY0sO6Tib6uenyw/ryV2fHk7INiGfTXgydg59nx2HlTG3s8e+PQO9HaOD8es++je3RCW5L9S7e82wvuXLp53/LS7c1sJpnSdje/YdQXbF//Rq6/ZPZCcvQ3cnfZ7Zjr5vN+y9M9k+4Z9jvg5n6z4w7eHNwR5JbFws7mdsoHu+XJ73lBkJ/wlmdxPNlq/4bglLLVvtn58ZgdzOy5O3+8vfuD+OB3/o/W7h+Ox+4H9wXeOIpPxtD50RylboH34zpZ3amE0mEJ1XcEwzLa9XdLKf1MKc26UlpYDqWdUtlSWt+vlGanXEqL48st/XFrdMLnrfJ4zH5bKQ3GZGcUn4wTquNxwsFdQzR2yWlavT4eq9+C/NFj20UefA2hP3bE3RcRf/mtFeqvZ+lFfn5GL7JzdAnn9os0u6D5RZbbUcNx130KWDi7/B7kv09dT9zTeeZTc8kaPtt+lt39nwynN3RHKhVt1Fv9O35k8hzIcv2YRG4SxYHv4iDRc+xmliS+G2E3ICQK/QgPvx4YWngy/BbVfPLd/fel7/8HUEsHCKNA+swOCQAAWzUAAFBLAQIUABQACAgIAChaLEBFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgAKFosQKNA+swOCQAAWzUAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACmCQAAAAA=" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
@@ Rad 90: / Rad 89: @@
 === Bevis som utgår från distributiva lagen ===
- x(c+d) = xc+xd
+: <Math> x(c+d) = xc+xd</Math>
+<br />
+Antag att <Math>x = a+b</Math> och sätt in i uttrycket ovan.
+:<Math> (a+b) c+(a+b)d</Math>
-Antag att x = a+b och sätt in i uttrycket ovan.
+:<Math>  c(a+b)+d(a+b)</Math>
- (a+b)c+(a+b)d
+:<Math>  ca+cb+da+db</Math>
- c(a+b)+d(a+b)
-  ca+cb+da+db
- ac+bc+ad+bd     V.S.B.
-Läs om [http://www.webbmatte.se/display_page.php?id=35&on_menu=231&page_id_to_fetch=668&lang=arabic&no_cache=163542237# distrributiva lagen på wwebbmatte].
+:<Math>  ac+bc+ad+bd  </Math>   V.S.B.
+<br />
+Läs om [http://www.webbmatte.se/display_page.php?id=35&on_menu=231&page_id_to_fetch=668&lang=arabic&no_cache=163542237# distributiva lagen på wwebbmatte].
 {{Khanruta|Hitta faktorerna till ett uttryck:
 [http://www.khanacademy.org/math/algebra/quadtratics/e/solving_quadratics_by_factoring solving quadratics by factoring]}}
+'''Öva hos OlleH''': http://olleh.se/start/frageprogramMa3.php
 == Kvadreringsregeln ==
+{{flipp| - }} {{TE12A|2}}{{Malruta|Du ska lära dig kvadreringsreglerna. Det är mycket viktigt.}}
+{{:kvadreringsregeln}}
+== En första läxa ==
+Det är viktigt att vi kommer igång med att lära oss Geogebra.
-{{:kvadreringsregeln}}
+Första naturliga ingången är egentligen räta linjen där det blir en tydlig koppling mellan funktion och utseende.
+=== GGB-uppgift 1 ===
+Ladda ner programmet.
+Skriv in en valfri räta linjens funktion.
+Ändra färg och tjocklek på grafen.
+Ändra så att grafens egenskap syns.
+Mejla filen till din lärare.
 == Konjugatregeln ==
+{{flipp| - }} {{TE12A|3}}{{Malruta|Du ska lära dig konjugatregeln. Det är mycket viktigt.}}
 {{:konjugatregeln}}
-=== Diagnos 11 ===
+{{uppgruta|Diagnos 11
+* [http://wikiskola.se/images/Veckodiagnos_11.pdf Veckodiagnos 11]
+* [[Lösningar till diagnos 11]]
-[[Lösningar till diagnos 11]]
+'''Rättelse:''' I lösningen till uppgift 6 finns tyvärr inte med att lösningen även har en negativ rot. Detta kommer vi att gå in noggrannare på i avsnitt 1.3 som behandlar andragradsekvationer.
+}}
+=== Snabbdiagnos 1 ===
-'''Rättelse:''' I lösningen till uppgift 6 finns tyvärr inte med att lösningen även har en negativ rot. Detta kommer vi att gå in noggrannare på i avsnitt 1.3 som behandlar andragradsekvationer.
+{{print|[http://wikiskola.se/images/Snabbdiagnos1_kvadrerings.pdf snabbdiagnos1 kvadrerings- och konjugatreglerna]
+}}
 == Ekvationer med x<sup>2</sup>-term ==
+{{flipp| - }}{{lm2c|Ekvationer|25-29}}  {{TE12A|4}}
 '''Repetition'''
-Uppgiften från förra lektionen att göra Khan ett tagskulle kunna vara en vettig repetition av föregående vecka.
+Gör Khan-uppgiften från förra avsnittet om du inte redan gjort det.
 === Intro ===
@@ Rad 133: / Rad 158: @@
 === Räkna uppgifterna: 1245-1258 ===
+{{läxa|Gör dessa uppgifter i GeoGebra
 * Uppgift 1251: Här gör du skissen i GeoGebra.
 * Uppgift 1257: Läs om en [http://sv.wikipedia.org/wiki/Ellips_%28matematik%29 Ellips på Wikipedia].
-** Pröva att göra en ellips i GeoGebra. Ledining skriv in ekvationen (x/a)^2+(y/b)^2=1. Välj själv värden på a och b.
+** Pröva att göra en ellips i GeoGebra. Ledining skriv in ekvationen (x/a)^2+(y/b)^2{{=}}1. Välj själv värden på a och b.
 ** Sök på Ellipse på GeoGebraTube.org. [[Inte ett facit till ellipsen]].
 ** Titta på en ellips i Wolfram|Alpha. Skriv in en formel eller skriv ordet Ellipse. [http://www.wolframalpha.com/input/?i=%28x%2F2%29^2%2B%28y%2F11%29^2%3D1 fuskväg]
+}}
-= Andragradsekvationer =
+=== En laborativ datorövning på pascals triangel ===
-Vi repeterar föregående avsnitt genom denna övning:
+{{transclude|{{:Pascals_triangel}}}}
-=== Övning: Pascals triangel ===
+= Andragradsekvationer =
-Gör övningen på sidan 24-25. Titta även på [http://sv.wikipedia.org/wiki/Pascals_triangel Wikipedia om Pascals triangel].
+== Enkla andragradsekvationer ==
+{{flipp| - }}{{lm2c|pq-formeln|30-32 och 35-38}}  {{TE12A|5}}
-'''Inlämning:''' Vi gör övningen på uppkopierat papper med inlämning och rättning.
-När du är klar med uppgiften jobbar du med Khan Academy. Länkar finns på föregående avsnitt.
-'''Lösning:''' Så här utvecklar du [[Pascal-algebra|(a+b)<sup>4</sup>]]
-<html><iframe src="http://phet.colorado.edu/sims/plinko-probability/plinko-probability_en.html" width="800" height="600"></iframe></html>
-'''Länkar:'''
-Här finns lite om [http://www.mathsisfun.com/pascals-triangle.html Pascals triangel] och[http://mathforum.org/workshops/usi/pascal/index.html idéer om triangeln]. Här finns [http://www.mathsisfun.com/pascals-triangle.html trianglar att skriva ut] m.m.
-Illustration av normalfördelning finns [http://www.mathsisfun.com/data/quincunx.html här].
-== Enkla andragradsekvationer ==
+{{#ev:youtube| Aa7M6Vzs71U}}
+Av Daniel Barker.
 Den här behöver man fundera på en stund. [http://www.geogebratube.org/student/m358 Quadratic equations in early Baghdad]
@@ Rad 175: / Rad 190: @@
 I båda fallen blir det en positiv och en negativ rot som svar (eller cdel av svaret men det blir inga imaginära tal eller komplexa rötter i detta avsnitt.
-== Kvadratkomplettering ==
+== Fullständiga andragradsekvationer ==
+=== pq-formeln - Förklaring===
+{{Malruta|Du ska lära dig pq-formeln. Det är mycket viktigt.}}
+En generell beskrivning av en andragradsekvation ser ut så här:
-=== '''Uppgift:''' Khan Academy ===
+: <math> x^2 + px + q = 0 </math>
-Lös dessa [http://www.khanacademy.org/exercise/solving_quadratics_by_factoring Khan, relativt enkla andragradsekvationer]. De kan lösas genom att gissa eller faktorisera.
+där p och q är tal (siffror) i den speciella ekvationen.
-''' Härledning av rotformeln '''
+Den allmänna ekvationen har lösningen:
-   <math> y = ax^2+bx+c = 0, a \ne 0 </math>
+: <math> x=-p/2 \pm \sqrt{(p/2)^2-q} </math>
-   Vi multiplicerar ekvationen med <math>4a \ne 0</math>
-   <math> 4a^2x^2 + 4abx + 4ac = 0 </math>
-   vi subtraherar <math>4ac</math> och skriver om
-   <math> (2ax)^2 + 4abx = -4ac </math>
-   då ser vi att det fattas <math>b^2</math> för kvadratkomplettering - adderas till bägge sidor
-   <math> (2ax)^2 + 2(2ax)b + b^2 = b^2-4ac </math>
-   <math> (2ax + b)^2 = b^2-4ac </math>
-   <math> D = b^2-4ac </math>
-   D kallas för diskriminanten.  Om den är positiv eller noll så har vi en lösning.
-   Om den är lika med noll blir det en dubbelrot annars blir det två reella rötter.
-   Om diskriminanten är mindre än noll saknas reella lösningar.
-   Lägg märke till att toppen på parabeln finns i punkten :
-   <math> (x=-\frac{b}{2a} , f(-\frac{b}{2a})) </math>
-   Vi löser vidare så här:
-   <math> 2ax + b = \pm \sqrt{b^2-4ac} </math>
-   Vi subtraherar <math>b</math> från bägge sidor.
-   <math> 2ax  = - b \pm \sqrt{b^2-4ac} </math>
-   Vi dividerar med <math>2a \ne 0</math> :
-   <math> x  = \frac{-b\pm \sqrt{b^2-4ac}}{2a} </math>
-   man kan sedan konstatera att :
-   <math> x_1  = \frac{-b - \sqrt{b^2-4ac}}{2a} </math>
-   och
-   <math> x_2  = \frac{-b + \sqrt{b^2-4ac}}{2a}</math>
-   Nu är vi klara.
-   Ibland kan det vara bra att veta att man om reella rötter saknas D < 0
+Om du vill lösa en ekvation behöver du bara ta reda på vad p och q motsvaras av i din ekvation och sedan sätter du in dessa siffror i formeln ovan.
-   löser de komplexa (imaginära) rötterna så här :
-   <math> z  = \frac{-b\pm i\cdot \sqrt{4ac-b^2}}{2a} </math>
-== Fullständiga andragradsekvationer ==
+Tänk på att det inte ska stå någor framför <math>x^2 </math>-termen
-=== pq-formeln ===
+'''Flipp:''' Se två filmer med Michael Bondestam:
-http://www.youtube.com/watch?v=eQZEtWY_4kE&feature=g-all pq-formeln
+{{#ev:youtube|eQZEtWY_4kE|340|left}}{{#ev:youtube|FVMWj3PTn7U|340|right}}
- x<sup>2</sup>+px+q=0
- x=-p/2+-((p/2)<sup>2</sup>-q)<sup>0.5</sup>
 <br>
 <pdf>Peequu-01022012090823.pdf</pdf>
-<br>
-<br>
-Se en film med Michael Bondestam:
-<youtube>eQZEtWY_4kE</youtube>
 <br>
 '''Räkna själv'''
@@ Rad 260: / Rad 225: @@
 <youtube>goYnB61nrjg</youtube>
 <br>
+== Kvadratkomplettering ==
+{{flipp| - }}
+{{lm2c|Kvadratkomplettering|33-34}}  {{TE12A|6}}
+{{#ev:youtube|VacSvx3dRhs|340|right}}
+Man kan börja med kvadratkomplettering som en inledande förklaring till pq-formeln men det är lika bra att ge sig på pq-formeln direkt. Sedan kan man gå tillbaks till kvadratkompletteringen för att få ett bevis för att pq-formeln fungerar.
+=== '''Uppgift:'''  ===
+{{khanruta|'''Solving Quadratics by facoring'''
+Lös dessa [http://www.khanacademy.org/exercise/solving_quadratics_by_factoring Khan, relativt enkla andragradsekvationer]. De kan lösas genom att gissa eller faktorisera.
+Möjligen kan det vara svårt att veta hur de menar att man ska göra på vissa uppgifter. Ta reda på rötterna och faktorisera så går et bra.
+}}
+== Diagnos 2 med pq-formeln ==
+{{print|[http://wikiskola.se/images/Snabbdiagnos2_kvadrerings_och_pq.pdf Snabbdiagnos 2]}}
 == Andragradsekvationer och rötter ==
+{{flipp| - }}{{lm2c|Diverse|39-44}}  {{TE12A|7}}
+{{exruta|Lös ekvationen:
+:<math>x^2-8x+16=0</math>
+Vad händer?
+Pröva nu ekvationen:
+:<math>x^2-8x+17=0</math>
+här har vi en ekvation som saknar reella lösningar.
+}}
 [[Fil:Exempel1_sid_35_Ma2c.PNG|300px|right|CC By --[[Användare:Hakan|hakan]] 3 februari 2012 kl. 17.50 (UTC)]]
+{{defruta|
   En andragradsekvation kan ha
   två reella rötter ''eller''
   en dubbelrot ''eller''
   två komplexa rötter
+}}
-Detta är på sid 35-37 i boken.
+{{#ev:youtube|LTR1s87IC2I|320|right}}
-'''Diagnosen'''
+<ggb_applet width="809" height="321"  version="4.2" ggbBase64="UEsDBBQACAAIANRwPUIAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIANRwPUIAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7VhZb9tGEH5OfsWAT0lrU7vLO5ASJAGKpnCCoE6Log8FVuRK2pgiCR6SHOTHd2aXpCg7DuI4fattaQ/OzrXfHPT8xWGbw07VjS6LhcNd5oAq0jLTxXrhdO3qPHZePH88X6tyrZa1hFVZb2W7cHxXOMdzuHJ5TId1tnAkX8YqC/h5wMXq3Jc8PU9SEZ7L5UpJLleeyAIH4NDoZ0X5Tm5VU8lUXaYbtZUXZSpbw3PTttWz2Wy/37uDdLes17P1eukemswB1LxoFk4/eYbsTg7tPUMuGOOzv95eWPbnumhaWaTKAbKq088fP5rvdZGVe9jrrN0snFigGRul1xsy08PFjIgqtLVSaat3qsGjk6Wxud1WjiGTBT1/ZGeQj+Y4kOmdzlS9cJgrfC9h0y8Hylqrou2JuRV6iwk/5RIm6GE+ft3BZT4blJrvtNpb7WhmFPdZEuFN6kYvc7VwVjJv0Dm6WNV4MWhX3eGyaa9ztZT1sJ5odIa/SKA/KeKF3rLeXDgi8s/i8Cxi7CwI2GDQKJdPhFqmo8xeh6PQfuNE6iDTiyYyOQqjT4gfo8wNoeihtixzw5RBkMDnzyCYYHBGA7eDwCEM7SNm95hnB2EH3w6BpfHtcd+S+pbGtzS+9xXf3s9Odg8744mdnIz4DJy0N4MHpDc3+tPg98vQLiMzcGYH3j+M6cv4K3ygRd53WcTDe+DlNkhHoULwo9AAoUl/5nNLpHgIQo8Cv2SlCL5spSfu49xbZg4yecC+1cjQf0jwf4dACtf/XuB8NqS6eR8I0GyItr/IVm0bSgFeYrIAcAgwSsIIgzYAnuAQUbQI4AH4AS55DCGNEXgUID54EAPRcQ9MrAcxfvkmeEIIkBdtRjaKwPMh8ICbDOED5gUwWQYzjvCQIgggwEMknZNYLwQ/xIUXg48KUn6JKIY9PIdrFC7A4+DRWR6BCCEUEFGO4j6lrjAm3ZGpgJBBSEcxSWGCsskJT8TgkTUYVFXZ6NG5G5VX460YP+qi6toT36XbbJi25Q3qrEyvXt3wtZJNO8yRCKvRsXTa6nRSWR/Nc7lUOfYflwQDgJ3MKZwM/1VZtDBAQNi9dS2rjU6bS9W2eKqBj3InL2SrDr8gdTMoaESbgj9XXZrrTMviT8QIsSCGMNR/U1CG+u8xbqWkZVlnl9cNAgcOf6u6pGDmrheLiIfMT3ASYlNzbR8JEbjcSxIeYYn2IwrrJpWEeO65fsIiKjqJH0Yex/i77p+FLnYCYcK9IKZJEFvRajeaJg+qGXy5rimceu/T4k3zqsyPW1Wpi/a1rNquNs0cZqSajHpZrHNlfGuuHNui9GpZHi6tUz3L68N1hStmFViuX5d5WQMGpAjQyHU/Lu1oaEizkYoZGmYo2HBLOhuf80QYCjMu7Wio8Nqtar2lfDCTs0GMbkwaQeZTkBnMUJPVFbq9GBatTq+OlhL9u267RLj1x05Z8h/Ecj67AbDbgKPkZM+BmRJkrDYnUDTFaoAi9lN3QzFIXDb5ESMS/cB3k+mPP0IxYCdnWDiB4s1n3L8DixP8/Q/GsQ34kWh8KM/bcLxSdaFyC6UCL7Mru8am2TFVPpp3jXov283LIvtdrbE+vJdUoltkbUmPKmcq1Vs8aPd750m62D9QVbubqXWtBhNz8zJnXWuesimwb20bVr/U5fZNsfuAqLmh6nw22DNv0lpXhE5YYs9wpY74y3QjsePIpufQ+AatSKn6oSNbcqIDsms3ZW3e17CGoD0J/CaLTtYayzYiksI5V1t8y4LW4LLotqrW6XhD0rwHoo5dbwaP3N4Suh8olx+x2N3IMn2p3I2VDqnuQDDIvNpIev/rS1MurymPTDxmmL4ts0GBXnpOL46w1YWBMGzlgdpTZ8g2Pr2/49a557KTlJFgm3CNnZsbnOxi0K30QY3dALpNf0JAnaLjGEUtVukrfBFtTGvd9kFtJr/qLFPFqKksEFDmWjDJVRbalVI2KsaDFRpukskECv3V0CUdqhplEZPexyt08IEalieHp7CAwz9PxFM4xzbuJzjAzyBte3J6uauuMPhwjky+fpGTCPqWK2TfeIXse505dclsinjTDvX/V3n+L1BLBwhQu8auIgYAAAcSAABQSwECFAAUAAgACADUcD1C1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIANRwPUJQu8auIgYAAAcSAAAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAuQYAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
-Resultatet på diagnosen var inte bra. Ni behöver räkna mer! Från och med nu gäller ett beting för varje lektion. Det är uppgifter som ni måste göra och visa upp. Om ni inte har godkända upvisade uppgifter från någon lektion måste ni gå på extramatten. Betinget är att göra alla svarta uppgifter.
+{{Uppgruta|
+: Lös uppgifterna i denna gamla [http://wikiskola.se/images/Veckodiagnos12.pdf Diagnos 12]
-Genomgång av diagnosen: [[Facit till Diagnos 12]]
+: Genomgång av diagnosen: [[Facit till Diagnos 12]]
+}}
 == Komplexa tal ==
@@ Rad 281: / Rad 285: @@
 === Teori ===
+{{defruta|'''Komplexa tal'''
+<br />
+:<math>\sqrt{-1} = i </math>
- Roten ur -1 = i.
+: <math> i^2 = -1 </math>
- i<sup>2</sup> = -1
+<br />
-Imaginärdel, realdel
- z = a + bi
+Ett komplext tal består av en realdel <math>a</math> och en imaginärdel <math>b</math>.
+<br />
+: <math> z = a + bi </math>
+}}
+<br />
 '''Läs mer:''' [http://sv.wikipedia.org/wiki/Komplexa_tal Komplexa tal på wikipedia]
 === Vad ska man ha komplexa tal till? ===
+{{#ev:youtube|DHoRnxqnWrw|320|right|komplexa tal}}
 * Komplexa tal '''används''' när man räknar på växelström.
@@ Rad 302: / Rad 311: @@
 [http://www.wolframalpha.com/input/?i=x^2%2B3x%2B16%3D0 x<sup>2</sup>+3x+16=0] har också två komplexa rötter fast här beror varje rot av både en realdel och en imaginärdel.
+{{clear}}
 == Rotekvationer ==
+{{flipp| - }}{{lm2c|Diverse|45-49}}  {{TE12A|8}}
+{{#ev:youtube|8hY6gm_NTMg|320|right|Rotekvationen}}
 '''Teori'''
@@ Rad 309: / Rad 321: @@
 Rotekvationer innehåller x-termer och roten ur x-termer. Man löser dem genom att kvadrera båda leden.
-Viktigt att kolla om man har falska rötter.
+: <math> \sqrt{x+2} = x </math>
+Kvadrera båda sidorna:
+: <math> x+2 = x^2 </math>
+: <math> x^2 - x - 2 = 0 </math>
+: <math> x =  \frac{1}{2} \pm \sqrt{\frac{1}{4} + 2} </math>
+: <math> x =  \frac{1}{2} \pm \sqrt{\frac{1}{4} + \frac{8}{4}} </math>
+: <math> x =  \frac{1}{2} \pm \sqrt{\frac{9}{4}} </math>
-'''Berätta om SI'''
+: <math> x =  \frac{1}{2} \pm \frac{3}{2} </math>
-Vi har SI-lektioner på onsdagar 16.30.
+: <math> x_1 = - 1, x_2 = 2 </math>
-'''Supplemental Instruction'''- möten är ett komplement till övriga undervisningsmoment som föreläsningar och övningar. På SI-möten som hålls av en äldre elektroteknolog får du möjlighet att lära dig att bearbeta kursinnehållet för att öka förståelsen. SI-ledaren är i detta avseende inte en lärare utan en mötesledare för studenterna. På SI-möten lär sig studenterna att själva arbeta med kursen med målet att öka sin förståelse. SI-ledaren är i detta avseende inte en lärare utan snarare en mentor för studenterna.
+Viktigt att kolla om man har falska rötter.
-Meningen är att studenterna med hjälp av SI-ledaren lär sig terminologin inom ämnet, att själva prioritera inom kursen och att angripa problem. Målsättningen är att denna träning skall ge studenterna en metodik som de kan ha stor nytta av i senare kurser. Supplemental Instruction är ingen stödundervisning utan syftar till att förbättra alla studenters studieteknik och analytiska förmåga och därmed förbättra studieresultaten.
-'''Film'''
+<math>-1 </math> är en falsk rot eftersom den inte gör att vänster led och höger led blir lika i ursprungsekvationen.
-Rotekvationer med hjälp av substitution kunde vara ett alternativ att titta på.
+Svaret är alltså <math>x = 2</math>
+{{clear}}
 == Problemlösning med ekvationer ==
@@ Rad 347: / Rad 370: @@
 =Ekvationslösning med faktorisering =
-Måndagslektionen kommer att vigas åt utvärderingsåterkoppling och jag hinner blott gå igenom lösningen till Diagnosen.
+{{flipp| - }}{{lm2c|Faktorisering|50-56}}  {{TE12A|9-10}}
 Diagnosen blir läxa att göra om hemma och denna gång ska den ha alla rätt. Det gäller alla. Facit kommer upp på tisdag så kan alla rätta själva.
@@ Rad 356: / Rad 379: @@
 == Uppdelning i faktorer med konjugatregeln ==
+{{uppgruta|
 Först ska vi [[repetera konjugatregeln]] med ett lösblad där det är rad snabba uppgifter. Dessa uppgifter bör klaras av på mindre än tre minuter.
+}}
-Vi kör samma övning som i måndags ävan idag.
-Avsluta med att ge nästa lösblad som läxa .
 == Uppdelning i faktorer med kvadreringsreglerna ==
+{{uppgruta|
 Här ska vi också [[repetera kvadreringsreglerna]] med ett lösblad.
+}}
 == Faktorisering och ekvationer ==
@@ Rad 375: / Rad 397: @@
 == Dataövning - konsekutiva tal ==
+{{flipp| - }}{{lm2c|Konsekutiva tal|57}}
 [[Fil:Fredrik_problem_konsekutiva_tal.jpg|300px|right|Fredriks lösning.]]
@@ Rad 388: / Rad 411: @@
 * [[Media:Konsek_charles-13022012163848.pdf|Charlie i NV11]] löser det genom att hitta mönster i de tal han prövar med och ...
-== Prov tisdag vecka 7 ==
+== Prov onsdag vecka 6 ==
-'''Diagnos 14'''
+{{TE12A|11-12}}
+{{uppgruta|'''Diagnos 14'''
 * [[Media:Veckodiagnos14.pdf|Diagnos 14]]
 * [[Media:Veckodiagnos14-Facit.pdf|Diagnos 14 Facit]]
+}}
 '''Repetition på fredag och måndag'''
 '''Uppgift:''' Khan Academy
+{{khanruta|
 # [http://www.khanacademy.org/exercise/multiplying_expressions_1 Khan om hur man multiplicerar binom] ska du verkligen öva på.
-# Lös dessa [http://www.khanacademy.org/exercise/solving_quadratics_by_factoring Khan, relativt enkla andragradsekvationer]. De kan lösas genom att gissa eller faktorisera.
+}}
 '''Uppgifter'''
@@ Rad 411: / Rad 437: @@
 # Öva ekvationer (= Extrablad ekvationer): finns bara på papper
 # Faktorisering: finns bara på papper
+# Öva enkla andragradsekvationer:  finns bara på papper
+{{print|
+'''Nöt in detta som du måste kunna!'''
 # [[Media:Öva_konjugatregeln.pdf|Öva konjugatregeln]]
 # [[Media:Öva_kvadreringsreglerna.pdf|Öva kvadreringsreglerna]]
-# Öva enkla andragradsekvationer:  finns bara på papper
+# [[Media:Öva_pq-formeln.pdf|Öva pq-formeln]]
-# [[Media:Öva_pq-formeln.pdf|Öva pq-formeln]] <font color red>Senaste tillskottet</font color red>
+}}
 '''Provet''' skall vara tisdag vecka 7 (ligger på SchoolSoft).
-== Omprovet ==
+== Facit och bedömning ==
-Vi räknar klart det gamla provet (åtminstone E-uppgifterna) på extramatten och i slutet av lektionen gör vi ett förenklat prov med E-del för sig och C/A-del för sig.
-Så får vi se hur det går.

Algebra 2C: Skillnad mellan sidversioner

Versionen från 28 mars 2013 kl. 07.25

Varför ska man lära sig algebra?

Intro

Förenkling av uttryck

Ekvationer

Kvadrerings- och konjugatregler

Parentesmultiplikation

Multiplikationen är både algebra och geometri

Och nu med bokstäver

Bevis som utgår från distributiva lagen

Kvadreringsregeln

Första och andra kvadreringsreglerna

WolframAlpha Widget

En första läxa

GGB-uppgift 1

Konjugatregeln

Konjugatregeln

Film

Geometriskt bevis av konjugatregeln

Uppgifter

Snabbdiagnos 1

Ekvationer med x2-term

Intro

Räkna uppgifterna: 1245-1258

En laborativ datorövning på pascals triangel

Aktivitet

Lär mer

Andragradsekvationer

Enkla andragradsekvationer

Fullständiga andragradsekvationer

pq-formeln - Förklaring

Kvadratkomplettering

Uppgift:

Diagnos 2 med pq-formeln

Andragradsekvationer och rötter

Komplexa tal

Teori

Vad ska man ha komplexa tal till?

Komplexa rötter

Rotekvationer

Problemlösning med ekvationer

Professionell matte

Vad ska man ha andragradsekvationer till?

PhET

Ekvationslösning med faktorisering

Uppdelning i faktorer med konjugatregeln

Uppdelning i faktorer med kvadreringsreglerna

Faktorisering och ekvationer

Dataövning - konsekutiva tal

Prov onsdag vecka 6

Facit och bedömning

Navigeringsmeny

Sök

Ekvationer med x²-term