En längre mätning av temperaturen när vatten svalnar: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) (Skapade sidan med 'Här finns en fil med värden från en längre mätning. Dessa värden ligger här i GeoGebra och jag har försökt få till en kurvanpas...') |
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
||
| Rad 4: | Rad 4: | ||
<ggb_applet width="1016" height="599" version="4.0" ggbBase64="UEsDBBQACAAIAI24l0AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAI24l0AAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Z3rc5tIEsA/Z/+KLj5c7V5hm+FNTsqWwM/EedpJrnJ1d4UFllgj0ALyY2/vf7+eGfGQxtmEdchyYati8Zie6ZkfPT2tRpDRj7eLGK7DLI/SZCyRXUWCMJmmQZTMxtKquNyxpR+ffDeaheksvMh8uEyzhV+MJZ1KRsFY8i/V0DcUf8cxLvUdXbHsHduZWjuqYWgXoU2moW5JALd59DhJX/iLMF/60/BsOg8X/mk69QumeF4Uy8d7ezc3N7ulqt00m+3NZhe7t3kgAXYzycfSeucxNrdR6UZj4qqikL2/Pz/lze9ESV74yTSUgA5hFT357tHoJkqC9AZuoqCY44AVVZdgHkazOQ7K0mwJ9qjUEoksw2kRXYc51m0cskEXi6XExPyElj/iexBX45EgiK6jIMzGkrKrKo5jKo5mGRKkWRQmxVqKcG1CbbJRXdds3TINU/1I9dFe2Y3RdRTe8P7QPdZVFLqO8ugiDrHb2QpZRMllhtdhLF36cY7HeXEXhxd+Vp1odETWsDz6BYV13ZGAw6PYFJn+mfinK0o5jEopMi3SNGaNKvDrr6AqqgIy3RC+UXFjmrxI4ecUjW9UvtH5xuAyOq+uc1Gdy+hcRtceNkZSjlHT1c8fo/oQpRVWlRiiStW4XyUxGzrXbVZKeR9+a6ClTmIotU5Uxf6xP0GjprbQyI8fptDUv8oQR3vlVBmtDRXyOZVdX8kiXOTUdDUHDIdaIAEDzdS00OAMIA5uLBXQMIEYoBt4SGww6dYCzcICHTSwgcoRDZidGjZ+6BZrzAQDG6NnLZweQFCRDoYGhJm3DmjUwKYIThdVQwnDAAMrUfVEpU1oJugmHmk26NhHOjssgoIaVsRjVK+CRkCjlYkFqgkmbY/odNaZNu06NqmCqYBJaIM4wXBy8YmF8jZodDTmGleULFfFBqLpIih3i3RZXQuURn9Uu0vunza86aNR7F+EMa4wZ/RKAlz7MZ0RTNFlmhRQXkSdn5tl/nIeTfOzsCiwVg4/+df+qV+Et4conZe6mew0TfJXWVp4abxaJDnANI2Vqs9pTBr7atVrPNAaBXqzwGgUmI196169KZbAKg9Rf5rlpbgfBCdUonYNSPJlEt+5WehfLdNocxijPbZYjcLVNI6CyE/eobFSLZQLlGsX88jl0mVYdtmRNAvO7nK0YLj9EGYpljm7mm07DrFM9C6WquJVveNFNrF2dWJZmmLYGiE2luRTn849bddwLGLptqEZhm0pNvqpu3WZtas4iuoYhoIitqlrBtcdXleXyL8Nq9HPsiho7p/kbhoHFQs2fM9fFquMRR3ocjI6qEkyi0NmImxi45I+vbpIb8+4bWi8rfO7JR4pXP/FjGEHdA0YfqAAbhV0KBfUIawNjHasklKYjMIklNLYomCrHIME3gZumQzaLu/YepikHCNRSiVRztyZIm1MGmb4NDpYJVFxWh4U0fSqHieVf7FaXISV+Ww2Sb5Qk6O9LfMa5Uu0xiCfh2Fxr8Gx5VEwOKx06YVxfNYUtUktqa6tIw9j6gPSBGB+Ns3SOGZ8rhv7UzZruQmwBXHN279LV9Qt4DgOMQBdxb7b8P/09FHDxujxMW/VrdclevbdvWdd1JWH2SuMouKNRrkTOUYo4UaFN9g+OwnVBI/j9OYMfVzkxwdBVKR171jROS4y59GymhLhzyssfYObKAuDjakvXIXRVZhhz9ZeBqfXKl3l3Gk2HFCAuhd4yAvWntOnU+gtGgY/G4SzLCztKWZRNjdjVqo0HYhwmjV1mKWLk+T6HOfnVgdGe2UvR/k0i5bUC8AFrsxX9fAwqM19XNg3xkvdIjLhhlFEBTVZhLYq5pQh1kE/j1vqDW+RTE6/qJRGP0Erw7Nj6S8/r9Lib0UU8B3WMFrbAmNlKJiHwMWikBr1mEHipYT04ie0yjqW4BINsCjwEX+Bl3Y592mIrlR2ijbRpMaae54GmyzZIocWF13W5sa9mrkOb9aiOEf5KO4dvrs5/HPk7SdX8I/U++fncXC/DQ7eNof82s+KFhy8/0sOG+NJVgusP61NXGVDQi2rUlfZqy83TPKZwySlC0EPxeY5RidLvjItw5CvacV6IYclNsfigEZn/NVtFEd+dsfbayxhn4nDFXA46pB5eCIPbcg8Jto2j0GbhyvgsJ0h8/AEHg4ZMo+Jvs1j0N7DFXDY9pB5eCIPZ9cYLo+Jsc3DHLJ5uAIOe9A8vD95bE4Xc5uHNWQcroDDNobMw/uTx+Z0sbZ5kEG7D1fgYQ07GhN5DNo+JrYwXwb95dYVeFiDXm89kYc+6G8vjpAbG/R66wo8LH3IPDyRx6DvNUyIImTHBg3EFYFYZMge1ROBmINecieECFNm0DGqKwIxBx2kevcA0YbsQyZEuIWrD/uepQjENIdsId49QAYdh0yIcBtXH/Sy64pAzGF/lRGBGIPOHU6IcCtXH3Qc4opAhh2HeCIQwxoykAkRb+cO2qm6IhBj0D8X8kQg+qAzqhMi3NIlxsDnjEBEV4bsVT0RiDZoJzIh4m1/a9BEXJGINujg3bsHyLf+s2XxGbH1s0HfT1QZXPWHUgd76pQ/r7xJcV1QVf8ErPoJzY+xYo+g/t5Hg9jTeDnc8qpwt35wBX4ZS9WlZD1mj1/y4Kp5dus5vk88UFax0pCV1paV2xtW6poVe2qhG1ZexUpHVnpbVl5vWGklK7szVvsVKwNZGW1Z7feGlVmyMjtjdVCxMpGV2ZbVQW9YWSUrozNWhxUrC1lZbVkd9oYVKQ3L6m4SHlWwbIRlt4V11B9YTgnL6gzWcQXLQVhOW1jHvYHFfqrFYOmdwTqpYBEFaRGlLa6T3uDSyiiL/UClG1xPa1yE4iJtcT3tD67Sb5ndBVrPalw0gietQ/hnvcGll3EpuzHdDa7TGhcN4knrKP60P7jKEMLsznc9r3HROJ60DuSfi7g2Xszz9WiVyyK7H9UNrRc1LRrJk9ah/Iu+0GK3ZCgtdiuiG1ova1o0lietg/mXfaHFs/EUF8tCd4PrVY2LhvOkdTz/qje4rPJLtdZdPH8a5YVfvvnmPxMkJoMnw74MBzIcynAkw7EMJzI8leGZDKcyPJfhhQwvZXj13/tgxtigtNX6QzKFRBFzhS2R1i9aK+bR9CpBAuzlYFWakO4cR0EQJlV+cQuwdj/gHbJNeJouFn4SQMJeNXkYFUdZelPMGQL++kNfqbjwIa+K8vQlb23dhoD2cpWwF1zV4P7YFw615/pbtghjaba2w9n3tz/AGBwd/grKruOo/8ITkmhrApDZJ+Zutzx+f076y5IcS6+b6Wqvdaz7ui8usMpWd7e8vmlmq73Wce6bvqAqvxSwV8p0g+qsmaz2Wse4Z31BVeWqnc6ikPNmrtprHeCe9wXVV0hVv22mqr3W0e3bvqD6Cpnqd81Mtdc6sn3XF1R1oro7s3rfTFR7rRPV73vDqspT6515qw/NPLXXOk/9oS+s6jS10pldTf5NNhLVXvtENW2iL9mxKlVtdncbxG0iIxRZ62S12ydkVbq6uxSZ10RGY/j2CWuvR8jqlHV3E3O/iYzG8u2T1vt9QlbGE0Z3yZ+DJjIa07dPXB/0CVm5VLJHBzr6sUATGY3t22evD3uErEpg691FrUdNZDTGb5/CPuoRsjqLrXWXlThuMqPBfvs89nGfmNWp7O7SEyypqpap7NcyvJHhTIZzGd7K8E6G9zJ8kAGDLxlc+uHRj336cUA/DunHEf1Acp+Z2lYfkm/8djPb6//gpJHZnvPWPjuzPf9DE7kPS8fuNf8zCnpc/l90T/4HUEsHCMfYH6EcCwAAKG8AAFBLAQIUABQACAAIAI24l0DWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAjbiXQMfYH6EcCwAAKG8AAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACzCwAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | <ggb_applet width="1016" height="599" version="4.0" ggbBase64="UEsDBBQACAAIAI24l0AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAI24l0AAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Z3rc5tIEsA/Z/+KLj5c7V5hm+FNTsqWwM/EedpJrnJ1d4UFllgj0ALyY2/vf7+eGfGQxtmEdchyYati8Zie6ZkfPT2tRpDRj7eLGK7DLI/SZCyRXUWCMJmmQZTMxtKquNyxpR+ffDeaheksvMh8uEyzhV+MJZ1KRsFY8i/V0DcUf8cxLvUdXbHsHduZWjuqYWgXoU2moW5JALd59DhJX/iLMF/60/BsOg8X/mk69QumeF4Uy8d7ezc3N7ulqt00m+3NZhe7t3kgAXYzycfSeucxNrdR6UZj4qqikL2/Pz/lze9ESV74yTSUgA5hFT357tHoJkqC9AZuoqCY44AVVZdgHkazOQ7K0mwJ9qjUEoksw2kRXYc51m0cskEXi6XExPyElj/iexBX45EgiK6jIMzGkrKrKo5jKo5mGRKkWRQmxVqKcG1CbbJRXdds3TINU/1I9dFe2Y3RdRTe8P7QPdZVFLqO8ugiDrHb2QpZRMllhtdhLF36cY7HeXEXhxd+Vp1odETWsDz6BYV13ZGAw6PYFJn+mfinK0o5jEopMi3SNGaNKvDrr6AqqgIy3RC+UXFjmrxI4ecUjW9UvtH5xuAyOq+uc1Gdy+hcRtceNkZSjlHT1c8fo/oQpRVWlRiiStW4XyUxGzrXbVZKeR9+a6ClTmIotU5Uxf6xP0GjprbQyI8fptDUv8oQR3vlVBmtDRXyOZVdX8kiXOTUdDUHDIdaIAEDzdS00OAMIA5uLBXQMIEYoBt4SGww6dYCzcICHTSwgcoRDZidGjZ+6BZrzAQDG6NnLZweQFCRDoYGhJm3DmjUwKYIThdVQwnDAAMrUfVEpU1oJugmHmk26NhHOjssgoIaVsRjVK+CRkCjlYkFqgkmbY/odNaZNu06NqmCqYBJaIM4wXBy8YmF8jZodDTmGleULFfFBqLpIih3i3RZXQuURn9Uu0vunza86aNR7F+EMa4wZ/RKAlz7MZ0RTNFlmhRQXkSdn5tl/nIeTfOzsCiwVg4/+df+qV+Et4conZe6mew0TfJXWVp4abxaJDnANI2Vqs9pTBr7atVrPNAaBXqzwGgUmI196169KZbAKg9Rf5rlpbgfBCdUonYNSPJlEt+5WehfLdNocxijPbZYjcLVNI6CyE/eobFSLZQLlGsX88jl0mVYdtmRNAvO7nK0YLj9EGYpljm7mm07DrFM9C6WquJVveNFNrF2dWJZmmLYGiE2luRTn849bddwLGLptqEZhm0pNvqpu3WZtas4iuoYhoIitqlrBtcdXleXyL8Nq9HPsiho7p/kbhoHFQs2fM9fFquMRR3ocjI6qEkyi0NmImxi45I+vbpIb8+4bWi8rfO7JR4pXP/FjGEHdA0YfqAAbhV0KBfUIawNjHasklKYjMIklNLYomCrHIME3gZumQzaLu/YepikHCNRSiVRztyZIm1MGmb4NDpYJVFxWh4U0fSqHieVf7FaXISV+Ww2Sb5Qk6O9LfMa5Uu0xiCfh2Fxr8Gx5VEwOKx06YVxfNYUtUktqa6tIw9j6gPSBGB+Ns3SOGZ8rhv7UzZruQmwBXHN279LV9Qt4DgOMQBdxb7b8P/09FHDxujxMW/VrdclevbdvWdd1JWH2SuMouKNRrkTOUYo4UaFN9g+OwnVBI/j9OYMfVzkxwdBVKR171jROS4y59GymhLhzyssfYObKAuDjakvXIXRVZhhz9ZeBqfXKl3l3Gk2HFCAuhd4yAvWntOnU+gtGgY/G4SzLCztKWZRNjdjVqo0HYhwmjV1mKWLk+T6HOfnVgdGe2UvR/k0i5bUC8AFrsxX9fAwqM19XNg3xkvdIjLhhlFEBTVZhLYq5pQh1kE/j1vqDW+RTE6/qJRGP0Erw7Nj6S8/r9Lib0UU8B3WMFrbAmNlKJiHwMWikBr1mEHipYT04ie0yjqW4BINsCjwEX+Bl3Y592mIrlR2ijbRpMaae54GmyzZIocWF13W5sa9mrkOb9aiOEf5KO4dvrs5/HPk7SdX8I/U++fncXC/DQ7eNof82s+KFhy8/0sOG+NJVgusP61NXGVDQi2rUlfZqy83TPKZwySlC0EPxeY5RidLvjItw5CvacV6IYclNsfigEZn/NVtFEd+dsfbayxhn4nDFXA46pB5eCIPbcg8Jto2j0GbhyvgsJ0h8/AEHg4ZMo+Jvs1j0N7DFXDY9pB5eCIPZ9cYLo+Jsc3DHLJ5uAIOe9A8vD95bE4Xc5uHNWQcroDDNobMw/uTx+Z0sbZ5kEG7D1fgYQ07GhN5DNo+JrYwXwb95dYVeFiDXm89kYc+6G8vjpAbG/R66wo8LH3IPDyRx6DvNUyIImTHBg3EFYFYZMge1ROBmINecieECFNm0DGqKwIxBx2kevcA0YbsQyZEuIWrD/uepQjENIdsId49QAYdh0yIcBtXH/Sy64pAzGF/lRGBGIPOHU6IcCtXH3Qc4opAhh2HeCIQwxoykAkRb+cO2qm6IhBj0D8X8kQg+qAzqhMi3NIlxsDnjEBEV4bsVT0RiDZoJzIh4m1/a9BEXJGINujg3bsHyLf+s2XxGbH1s0HfT1QZXPWHUgd76pQ/r7xJcV1QVf8ErPoJzY+xYo+g/t5Hg9jTeDnc8qpwt35wBX4ZS9WlZD1mj1/y4Kp5dus5vk88UFax0pCV1paV2xtW6poVe2qhG1ZexUpHVnpbVl5vWGklK7szVvsVKwNZGW1Z7feGlVmyMjtjdVCxMpGV2ZbVQW9YWSUrozNWhxUrC1lZbVkd9oYVKQ3L6m4SHlWwbIRlt4V11B9YTgnL6gzWcQXLQVhOW1jHvYHFfqrFYOmdwTqpYBEFaRGlLa6T3uDSyiiL/UClG1xPa1yE4iJtcT3tD67Sb5ndBVrPalw0gietQ/hnvcGll3EpuzHdDa7TGhcN4knrKP60P7jKEMLsznc9r3HROJ60DuSfi7g2Xszz9WiVyyK7H9UNrRc1LRrJk9ah/Iu+0GK3ZCgtdiuiG1ova1o0lietg/mXfaHFs/EUF8tCd4PrVY2LhvOkdTz/qje4rPJLtdZdPH8a5YVfvvnmPxMkJoMnw74MBzIcynAkw7EMJzI8leGZDKcyPJfhhQwvZXj13/tgxtigtNX6QzKFRBFzhS2R1i9aK+bR9CpBAuzlYFWakO4cR0EQJlV+cQuwdj/gHbJNeJouFn4SQMJeNXkYFUdZelPMGQL++kNfqbjwIa+K8vQlb23dhoD2cpWwF1zV4P7YFw615/pbtghjaba2w9n3tz/AGBwd/grKruOo/8ITkmhrApDZJ+Zutzx+f076y5IcS6+b6Wqvdaz7ui8usMpWd7e8vmlmq73Wce6bvqAqvxSwV8p0g+qsmaz2Wse4Z31BVeWqnc6ikPNmrtprHeCe9wXVV0hVv22mqr3W0e3bvqD6Cpnqd81Mtdc6sn3XF1R1oro7s3rfTFR7rRPV73vDqspT6515qw/NPLXXOk/9oS+s6jS10pldTf5NNhLVXvtENW2iL9mxKlVtdncbxG0iIxRZ62S12ydkVbq6uxSZ10RGY/j2CWuvR8jqlHV3E3O/iYzG8u2T1vt9QlbGE0Z3yZ+DJjIa07dPXB/0CVm5VLJHBzr6sUATGY3t22evD3uErEpg691FrUdNZDTGb5/CPuoRsjqLrXWXlThuMqPBfvs89nGfmNWp7O7SEyypqpap7NcyvJHhTIZzGd7K8E6G9zJ8kAGDLxlc+uHRj336cUA/DunHEf1Acp+Z2lYfkm/8djPb6//gpJHZnvPWPjuzPf9DE7kPS8fuNf8zCnpc/l90T/4HUEsHCMfYH6EcCwAAKG8AAFBLAQIUABQACAAIAI24l0DWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAjbiXQMfYH6EcCwAAKG8AAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACzCwAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
{{clear}} | |||
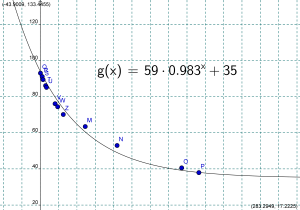
Termometern stod på burkens botten. Det ger upphov till en linjär komponent i funktionen. Så här ser en bättre kurvanpassning ut: [[Fil:Svalnande_vatten.png|thumb]] | Termometern stod på burkens botten. Det ger upphov till en linjär komponent i funktionen. Så här ser en bättre kurvanpassning ut: [[Fil:Svalnande_vatten.png|thumb]] | ||
Versionen från 25 april 2012 kl. 11.47
Här finns en fil med värden från en längre mätning.
Dessa värden ligger här i GeoGebra och jag har försökt få till en kurvanpassning med RegressionExp[] men det funkar inte så bra. Fundera på varför exponentialfunktionen passar så dåligt till värdena.
<ggb_applet width="1016" height="599" version="4.0" ggbBase64="UEsDBBQACAAIAI24l0AAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAI24l0AAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Z3rc5tIEsA/Z/+KLj5c7V5hm+FNTsqWwM/EedpJrnJ1d4UFllgj0ALyY2/vf7+eGfGQxtmEdchyYati8Zie6ZkfPT2tRpDRj7eLGK7DLI/SZCyRXUWCMJmmQZTMxtKquNyxpR+ffDeaheksvMh8uEyzhV+MJZ1KRsFY8i/V0DcUf8cxLvUdXbHsHduZWjuqYWgXoU2moW5JALd59DhJX/iLMF/60/BsOg8X/mk69QumeF4Uy8d7ezc3N7ulqt00m+3NZhe7t3kgAXYzycfSeucxNrdR6UZj4qqikL2/Pz/lze9ESV74yTSUgA5hFT357tHoJkqC9AZuoqCY44AVVZdgHkazOQ7K0mwJ9qjUEoksw2kRXYc51m0cskEXi6XExPyElj/iexBX45EgiK6jIMzGkrKrKo5jKo5mGRKkWRQmxVqKcG1CbbJRXdds3TINU/1I9dFe2Y3RdRTe8P7QPdZVFLqO8ugiDrHb2QpZRMllhtdhLF36cY7HeXEXhxd+Vp1odETWsDz6BYV13ZGAw6PYFJn+mfinK0o5jEopMi3SNGaNKvDrr6AqqgIy3RC+UXFjmrxI4ecUjW9UvtH5xuAyOq+uc1Gdy+hcRtceNkZSjlHT1c8fo/oQpRVWlRiiStW4XyUxGzrXbVZKeR9+a6ClTmIotU5Uxf6xP0GjprbQyI8fptDUv8oQR3vlVBmtDRXyOZVdX8kiXOTUdDUHDIdaIAEDzdS00OAMIA5uLBXQMIEYoBt4SGww6dYCzcICHTSwgcoRDZidGjZ+6BZrzAQDG6NnLZweQFCRDoYGhJm3DmjUwKYIThdVQwnDAAMrUfVEpU1oJugmHmk26NhHOjssgoIaVsRjVK+CRkCjlYkFqgkmbY/odNaZNu06NqmCqYBJaIM4wXBy8YmF8jZodDTmGleULFfFBqLpIih3i3RZXQuURn9Uu0vunza86aNR7F+EMa4wZ/RKAlz7MZ0RTNFlmhRQXkSdn5tl/nIeTfOzsCiwVg4/+df+qV+Et4conZe6mew0TfJXWVp4abxaJDnANI2Vqs9pTBr7atVrPNAaBXqzwGgUmI196169KZbAKg9Rf5rlpbgfBCdUonYNSPJlEt+5WehfLdNocxijPbZYjcLVNI6CyE/eobFSLZQLlGsX88jl0mVYdtmRNAvO7nK0YLj9EGYpljm7mm07DrFM9C6WquJVveNFNrF2dWJZmmLYGiE2luRTn849bddwLGLptqEZhm0pNvqpu3WZtas4iuoYhoIitqlrBtcdXleXyL8Nq9HPsiho7p/kbhoHFQs2fM9fFquMRR3ocjI6qEkyi0NmImxi45I+vbpIb8+4bWi8rfO7JR4pXP/FjGEHdA0YfqAAbhV0KBfUIawNjHasklKYjMIklNLYomCrHIME3gZumQzaLu/YepikHCNRSiVRztyZIm1MGmb4NDpYJVFxWh4U0fSqHieVf7FaXISV+Ww2Sb5Qk6O9LfMa5Uu0xiCfh2Fxr8Gx5VEwOKx06YVxfNYUtUktqa6tIw9j6gPSBGB+Ns3SOGZ8rhv7UzZruQmwBXHN279LV9Qt4DgOMQBdxb7b8P/09FHDxujxMW/VrdclevbdvWdd1JWH2SuMouKNRrkTOUYo4UaFN9g+OwnVBI/j9OYMfVzkxwdBVKR171jROS4y59GymhLhzyssfYObKAuDjakvXIXRVZhhz9ZeBqfXKl3l3Gk2HFCAuhd4yAvWntOnU+gtGgY/G4SzLCztKWZRNjdjVqo0HYhwmjV1mKWLk+T6HOfnVgdGe2UvR/k0i5bUC8AFrsxX9fAwqM19XNg3xkvdIjLhhlFEBTVZhLYq5pQh1kE/j1vqDW+RTE6/qJRGP0Erw7Nj6S8/r9Lib0UU8B3WMFrbAmNlKJiHwMWikBr1mEHipYT04ie0yjqW4BINsCjwEX+Bl3Y592mIrlR2ijbRpMaae54GmyzZIocWF13W5sa9mrkOb9aiOEf5KO4dvrs5/HPk7SdX8I/U++fncXC/DQ7eNof82s+KFhy8/0sOG+NJVgusP61NXGVDQi2rUlfZqy83TPKZwySlC0EPxeY5RidLvjItw5CvacV6IYclNsfigEZn/NVtFEd+dsfbayxhn4nDFXA46pB5eCIPbcg8Jto2j0GbhyvgsJ0h8/AEHg4ZMo+Jvs1j0N7DFXDY9pB5eCIPZ9cYLo+Jsc3DHLJ5uAIOe9A8vD95bE4Xc5uHNWQcroDDNobMw/uTx+Z0sbZ5kEG7D1fgYQ07GhN5DNo+JrYwXwb95dYVeFiDXm89kYc+6G8vjpAbG/R66wo8LH3IPDyRx6DvNUyIImTHBg3EFYFYZMge1ROBmINecieECFNm0DGqKwIxBx2kevcA0YbsQyZEuIWrD/uepQjENIdsId49QAYdh0yIcBtXH/Sy64pAzGF/lRGBGIPOHU6IcCtXH3Qc4opAhh2HeCIQwxoykAkRb+cO2qm6IhBj0D8X8kQg+qAzqhMi3NIlxsDnjEBEV4bsVT0RiDZoJzIh4m1/a9BEXJGINujg3bsHyLf+s2XxGbH1s0HfT1QZXPWHUgd76pQ/r7xJcV1QVf8ErPoJzY+xYo+g/t5Hg9jTeDnc8qpwt35wBX4ZS9WlZD1mj1/y4Kp5dus5vk88UFax0pCV1paV2xtW6poVe2qhG1ZexUpHVnpbVl5vWGklK7szVvsVKwNZGW1Z7feGlVmyMjtjdVCxMpGV2ZbVQW9YWSUrozNWhxUrC1lZbVkd9oYVKQ3L6m4SHlWwbIRlt4V11B9YTgnL6gzWcQXLQVhOW1jHvYHFfqrFYOmdwTqpYBEFaRGlLa6T3uDSyiiL/UClG1xPa1yE4iJtcT3tD67Sb5ndBVrPalw0gietQ/hnvcGll3EpuzHdDa7TGhcN4knrKP60P7jKEMLsznc9r3HROJ60DuSfi7g2Xszz9WiVyyK7H9UNrRc1LRrJk9ah/Iu+0GK3ZCgtdiuiG1ova1o0lietg/mXfaHFs/EUF8tCd4PrVY2LhvOkdTz/qje4rPJLtdZdPH8a5YVfvvnmPxMkJoMnw74MBzIcynAkw7EMJzI8leGZDKcyPJfhhQwvZXj13/tgxtigtNX6QzKFRBFzhS2R1i9aK+bR9CpBAuzlYFWakO4cR0EQJlV+cQuwdj/gHbJNeJouFn4SQMJeNXkYFUdZelPMGQL++kNfqbjwIa+K8vQlb23dhoD2cpWwF1zV4P7YFw615/pbtghjaba2w9n3tz/AGBwd/grKruOo/8ITkmhrApDZJ+Zutzx+f076y5IcS6+b6Wqvdaz7ui8usMpWd7e8vmlmq73Wce6bvqAqvxSwV8p0g+qsmaz2Wse4Z31BVeWqnc6ikPNmrtprHeCe9wXVV0hVv22mqr3W0e3bvqD6Cpnqd81Mtdc6sn3XF1R1oro7s3rfTFR7rRPV73vDqspT6515qw/NPLXXOk/9oS+s6jS10pldTf5NNhLVXvtENW2iL9mxKlVtdncbxG0iIxRZ62S12ydkVbq6uxSZ10RGY/j2CWuvR8jqlHV3E3O/iYzG8u2T1vt9QlbGE0Z3yZ+DJjIa07dPXB/0CVm5VLJHBzr6sUATGY3t22evD3uErEpg691FrUdNZDTGb5/CPuoRsjqLrXWXlThuMqPBfvs89nGfmNWp7O7SEyypqpap7NcyvJHhTIZzGd7K8E6G9zJ8kAGDLxlc+uHRj336cUA/DunHEf1Acp+Z2lYfkm/8djPb6//gpJHZnvPWPjuzPf9DE7kPS8fuNf8zCnpc/l90T/4HUEsHCMfYH6EcCwAAKG8AAFBLAQIUABQACAAIAI24l0DWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAjbiXQMfYH6EcCwAAKG8AAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACzCwAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
Termometern stod på burkens botten. Det ger upphov till en linjär komponent i funktionen. Så här ser en bättre kurvanpassning ut: