Geometri 2C: Skillnad mellan sidversioner
ViktorE (diskussion | bidrag) |
ViktorE (diskussion | bidrag) |
||
| Rad 125: | Rad 125: | ||
'''Definition''' | '''Definition''' | ||
Skala = En sträcka i bilden / Motsvarande sträcka i verkligheten | Skala = En sträcka i bilden / Motsvarande sträcka i verkligheten | ||
'''Definition: Längdskala''' | '''Definition: Längdskala''' | ||
Längdskala = Bildens längd / Motsvarande längd i verkligheten | Längdskala = Bildens längd / Motsvarande längd i verkligheten | ||
[[Fil:1000px-Scale one to thousand volume.svg.png|thumb|247px]] | [[Fil:1000px-Scale one to thousand volume.svg.png|thumb|247px]] | ||
'''Definition: Areaskala''' | '''Definition: Areaskala''' | ||
Areaskala = Stor kvadratens area / Lilla kvadratens area | Areaskala = Stor kvadratens area / Lilla kvadratens area | ||
| Rad 138: | Rad 141: | ||
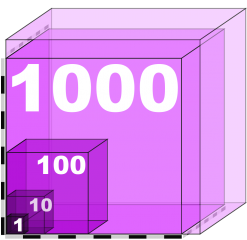
'''Definition: Volymskala''' | '''Definition: Volymskala''' | ||
Volymskala = Stora kubens volym / Lilla kubens volym | Volymskala = Stora kubens volym / Lilla kubens volym | ||
'''Länkar''' | '''Länkar''' | ||
Versionen från 20 februari 2012 kl. 18.48

En datauppgift
Inloggning på wikiskola
Ett användarnamn som är ditt exakta förnamn plus Initialen i ditt efternamn
Kunskapskrav
Betyget E
Eleven kan översiktligt beskriva innebörden av centrala begrepp med hjälp av några representationer samt översiktligt beskriva sambanden mellan begreppen. Dessutom växlar eleven med viss säkerhet mellan olika representationer.
Eleven kan föra enkla matematiska resonemang och värdera med enkla omdömen egna och andras resonemang ... ... Dessutom uttrycker sig eleven med viss säkerhet i tal, skrift och handling med inslag av matematiska symboler och andra representationer.
Genom att ge exempel relaterar eleven något i kursens innehåll till dess betydelse inom andra ämnen, yrkesliv, samhällsliv och matematikens kulturhistoria. Dessutom kan eleven föra enkla resonemang om exemplens relevans.
Eleverna bygger sidorna
Utifrån grundformen med en film en länk till Khan osv får eleverna uppgiften att bygga en sida var under kursen. ett avsnitt var alltså. Och detta gör de i början av kursen för att få ett hum om vad kursen handlar om. Det är sexton avsnitt i kap ett och det är 16 elever.
Jag har markerat i min mattebok vilka teoribitar som kan komma ifråga.
Minst:
- En film av Matteboken, Bondestam etc
- En Khanlänk
- En text
- En definition
- Ett exempel
- En uppgift
- En bild
- En länk till fler förklaringar
- En länk som knyter ant till matematikens kulturhistoria
- Ett försök att förklara vad man ska ha detta till
Editering
Editera under er egen rubrik. Inget kan gå fel. Allt går att rädda.
Titta på färdiga sidor hur man kan göra och härma wikikoden.
Vinklar
Läs Ma2C s. 66-70


Genomgång
Vinkelsumman och yttervinkeln finns visade på Geogebra.se
Definition: Vinkelsumma
Vinkelsumman i en triangel är 180o
Definition: Sidovinklar
Definition: Vertikalvinklar
- Figur 2a. Två räta linjer som korsar varandra i en gemensam punkt.

Definition: Alternatvinklar
Sats: Yttervinkelsatsen
Bevis: Yttervinkelsatsen
Länkar
Malin Christersson har en fin sajt där jag hittade en Geogebra om yttervinklar: http://www.malinc.se/math/basicgeometry/exterioranglesv.php
Likformighet och kongruens
s. 71 -74
AmmarA - Likformighet
Text om ..
Definition
Blablabetyder--
Länkar
TildaD - Kongruens
Text om kongruens..
Definition
Kongruens betyder--
Länkar
Längd, area och volymskala
s. 75- 79
Tisdag v 8.
Definition
Skala = En sträcka i bilden / Motsvarande sträcka i verkligheten
Definition: Längdskala
Längdskala = Bildens längd / Motsvarande längd i verkligheten
Definition: Areaskala
Areaskala = Stor kvadratens area / Lilla kvadratens area
Definition: Volymskala
Volymskala = Stora kubens volym / Lilla kubens volym
Länkar
- Scale of the Universe
- Skala på Wikipedia
- Längdskala och areaskala - Matteboken.se
- Skala och likformighet - Matteguiden.se
ViktorE Skala
Topptriangel- och transversalsatsen
Tisdag v 8.
NilsG Topptriangelsatsen
81- 85
Randvinklar och medelpunktsvinklar
86-91
DenisJ - Randvinkelsatsen
FredrikJ-Bisektrissatsen
Länkar
Text om Bisektrissatsen.....
Defenition...
Bisektrissatsen = AD / BD = AC / BC
Koordinatgeometri
s. 92- 101
RikardM - Avståndsformeln
WilliamM - Mittpunktsformeln

Mittpunktsformeln är en mattematisk ekvation. Två punkter P1 och P2 som kan ligga precis var som helst i ett kordinatsystem, med hjälp av mittpunktsformeln bestämma punkten mitt emellan Punkt1 och Punkt2 som har benämningen M.
Definition 1:
(X1,Y1) och (X2,Y2) (Xm,Ym)= (X1+X2/2),(Y1+Y2/2) Förklaras i videon
Definition 2:
Det gick inte att placera definitionen från Wikipedia, eftersom den inte stöds, gå in på länken och se efter själv:Wikipedia, Mittpunktsformeln O = Origo. M = Punkten mellan P1 och P2. P1 = Punkt1. P2 = Punkt2.
LÄNKAR
Film om Mittpunktsformeln Khan Acadamy
FelixN - y=kx+m
Riktningskoefficienten
s. 102 - 104
SamN - riktningskoefficienten

Om man känner till två punkters koordinater kan man rita linjen i ett koordinatsystem. Man kan även bestämma formeln för den räta linjens funktion. Två viktiga former är:
k är riktningskoefficitenten och anger funktionens lutning.
m är punkten där funktionen skär y-axel
http://www.matteguiden.se/wp-content/uploads/2010/01/linjes-lutning-4.png http://www.matteguiden.se/wp-content/uploads/2010/01/linjes-lutning-3.png
Definition
Y=kx+m
Länk
lov
Räta linjens ekvation
s. 105-109
HåkanE
Parallella och vinkelriitta linjer
s. 110- 112
SimonS - parallella och vinkelräta linjer
Allmän form (linjens ekvation)
s. 113- 115
Ekvationssystem (grafiskt)
s. 116-119
Här finns det plats för Håkan att skriva om annat som ska hända på lektionen än just det som som eleven nedan förbereder.
KevinS - ekvationssystem
- En film av Matteboken, Bondestam etc
- En Khanlänk
- En text
- En definition
- Ett exempel
- En uppgift
- En bild
- En länk till fler förklaringar
- En länk som knyter ant till matematikens kulturhistoria
- Ett försök att förklara vad man ska ha detta till
Ersättningsmetoden
s. 120-122
Här finns det plats för Håkan att skriva om annat som ska hända på lektionen än just det som som eleven nedan förbereder.
PatrikS - Ersättningsmetoden
Additionsmetoden
s. 123 -126
Här finns det plats för Håkan att skriva om annat som ska hända på lektionen än just det som som eleven nedan förbereder.
RichardS - Additionsmetoden
Lösning till ekvationssystem
s. 127- 128
Här finns det plats för Håkan att skriva om annat som ska hända på lektionen än just det som som eleven nedan förbereder.
JakubW - Lösning till ekvationssystem
Problemlösning med ekvationssystem
s. 129-132
Ekvationssystem med tre obekanta
s. 133-134

