Algebra 2C: Skillnad mellan sidversioner

Från Wikiskola
Hoppa till navigering Hoppa till sök
VisuellWikitext
Rad 190: Rad 190:


* Uppgift 1251: Här gör du skissen i GeoGebra.
* Uppgift 1251: Här gör du skissen i GeoGebra.
* Uppgift 1257: Läs om en Ellips på Wikipedia.
* Uppgift 1257: Läs om en [http://sv.wikipedia.org/wiki/Ellips_%28matematik%29 Ellips på Wikipedia].
** Pröva att göra en ellips i GeoGebra. Ledining skriv in ekvationen (x/a)^2+(x/b)^2=1. Välj själv värden på a och b.
** Sök på Ellipse på GeoGebraTube.org.
** Titta på en ellips i Wolfram|Alpha. Skriv in en formel eller skriv ordet Ellipse.


=== Övning: Pascals triangel ===
=== Övning: Pascals triangel ===

Versionen från 22 januari 2012 kl. 16.38

Kapitel 1 i boken Matematik 2C innehåller 16 delar vilket rimligen bör ta omkring 16 lektionstillfällen eller fyra veckor i anspråk.

Repetition

Mål för wikiskola på denna sida

Ett mål för denna kurs är att varje avsnitt om möjligt ska ha ett videoklipp med någon som förklarar, relevant länk till Khan samt en GGB el dyl som anknyter till bokens teoridel. Dessutom vore det fint med några egna övningsuppgifter och någon datorövning.

Intro

Kuriosa: Grafer på Google

Algebraintroti boken på sid 3

Gerolamo Cardano funderade över lösingen till följande ekvation 

Kan vi dela talet 8 i två delar så att deras produkt blir 25?
x(8-x) = 25

Ekvationen har följande rötter: 

x = 4 + rot(-9)
x = 4 - rot(-9)

Ekvationen kan skrivas om på detta sätt: 

8x - x2 = 25

x2 - 8x + 25 = 0

Men vad är roten ur -9? Det är ett imagint tal, som skrivs 3i. Kolla gärna Wolfram Alpha för en lösning till ekvationen ovan

Förenkling av uttryck

Sats: Distributiva lagen 

a(b+c) = ab + ac

Ekvationer

Vid lösning av ekvationer kan du tänka att det är tillåtet att göra samma sak på båda sidor av likhetstecknet. Du kan addera samma sak på båda sidorna. Eller subtrahera samma sak på båda sidorna. På samma sätt kan du multiplicera eller dividera med samma sak på båda sidorna.

Detta kan du använda för att förkorta bort något på ena sidan och resultatet blir att den saken byter upp på andra sidan men med motsatt tecken (plus blir minus osv).

På denna sida från Matteboken.se finns en förklaring skriva om hur man ändrar i ekvationer på detta sätt. Titta gärna på filmen på sidan också.

När man får kläm på det här sättet att ändra i ekvationer brukar man helt enkelt flytta över saker till andra sidan och byta tecken. På så sätt kan man ändra en ekvation så att man får sitt x (eller vilken variabel man nu vill lösa ut) ensamt på en sida.

Kvadrerings- och konjugatregler

Parentesmultiplikation

Multiplikationen är både algebra och geometri

(a+b)(c+d)=ac+ad+bc+bd

Hur funkar det om man multiplicerar två parenteser med varandra?

Först inleder vi med ett exempel med siffror

En övning som visar exemplet nedan i bilder. Ett tal kan delas upp i sin entalsdel och sin tiotalsdel innan en multiplikation. PowerPoint. Gånger av tvåsiffriga tal visas med hjälp av bilder. Detta är ett exempel från grundskolan. 

exempelvis 
12*13=(10+2)*(10+3)=100+30+20+6.

Repetition aritmetik: Pappersövning i skriftlig huvudräkning.

Tänk sedan att du gör samma sak med bokstäver 

(a+b)(c+d)=ac+ad+bc+bd


<ggb_applet width="796" height="511" version="4.0" ggbBase64="UEsDBBQACAgIAChaLEAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAAoWixAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1b747bNhL/nD4FoQ+HXWxsi9T/nLdFk7uiAZImQHKHw30pKIm2GUuiKlJeb9DHuXuSvtgNScmW7U32T5Oc10E2FMXhDGfmNzMkV5n+sC4LtGKN5KK6dPDYdRCrMpHzan7ptGo2ip0fvv9uOmdiztKGoploSqouHV9T8vzSmSVhMpvFeJRnLBr5LItHSZ6kozwnmEUsSGgWOQitJX9WiV9oyWRNM/YuW7CSvhIZVUbwQqn62WRydXU17kWNRTOfzOfpeC1zB8EyK3npdA/PgN3OpCvPkBPXxZN/vX5l2Y94JRWtMuYgrULLv//uyfSKV7m4Qlc8V4tLJ3Z9By0Yny9Ap9APHTTRRDUYpGaZ4ismYeqga3RWZe0YMlrp8Sf2CRUbdRyU8xXPWXPpuGPiRhHGvk+iOHTDJAwcJBrOKtUR407opGc3XXF2ZfnqJyMSlqmEKFKqWaLff0fEJS56qhtsGwJNGNoh175zPdsQ2/i2CSyNb6f7ltS3NL6l8T0HrbjkacHAw7SQYEJezRpw36Yv1XXBzHq6F1v18VPQSfKPQIxdwIm1uek81T8h/Ph6YLKrJB5IVU17T6G9yCgJ7y6S/ClFvY2aYXQokwSfUDP8jFCr9130xMHAtCDK/DU/BxK9z6m5L9H2bxPoxVpgFPs3Cgz9b6LidNKHyrSLDiQXmrZDj2Kl1PHiJShINOwxCiA2wghQHiCcQBMRBNGAcID8ALo4RqFuI+RFMOAjD8VI02EPmeAIYvjHjwyzEAXATL+NICYRBkE+CjyETUz5CCIJmbiEGCUeUAQBCmCSFo+JZuGFyA+h58XIhzXqkIwwEHowEfogniAPI09PxhEiIQo1P+zrUA9jvXRgSVDoohBrhhDVENE2moE+Rp7Wps9rvKpbtWOirMz7RyXqjS+AGvLRNu3Z/LSTFZ9MC5qyAgrFO+1JhFa00BFhBM1EpVDvRGLfzRtaL3gm3zGlYJZEH+iKvqKKrX8CatnLNrSZqOTbRqgXomjLSiKUicLdrFkUePBMNquGjjcY8IcDwWAgHDxHN8oVMIJayUC+aGRPTvP8pabYpgaw5JuquH7eMLqsBd9VYzoxNWfK2qzgOafVPwGsWoq2C+pLkElXfQnyY69fiGjyd9cSEIzW/2aNgFSFydj3SEKwG/ok9BIHXdsRL/TGQRBjD/s4IJHnQYmRGdWxFwXjIIxiQlwvCeMw0ZO6oZCMcRyGOHSjIPEJDgIrmq02HqJrtlV23ph6v+28lM9FsX1l9H9Ba9U2ZvcAybHRWv1YzQtmMGIiG0pztkzF+p0Fh2d5vb+uoefaFaRzY3cEuYHoAj3v2hTafpV6aRsq19C4hsLt0cbzzThOiKEwbWpbQwXwtUvrVMW9mtjtxXBpMprrdHHTZysNfl3p24qrV31H8Wy5VVVP+KUtU7aB0C5P/KV4Tid7GJsuWVOxooM0OLMVrbQROkB7zjJeQtcOdCah2l3/gAXYtzmbN6xfeGF2ZtZgZtQdovXgtWH1UyPKl9XqPWBhbwHTSb/KqcwaXmvMoRTKwJJtUZVzSaGK5MN5OgZB9UxXCzCP0qY5oxfp+Vl2kZ9DnLZqIcDtP//x3yWt0N8L2IlJxefADdIN2NRsBEWzlAvG1Hu2VoimYgUjr9tC8brgS1OJEF0h2ZYlgIhXokQ1bWDbxiRr0B//aWCjDK9VI/J22a2kKNByRfOG6QiQDQP1m4oikS3QUlQf2jlV8JIV1RhgyArteqMQK1gJnJEyUVC1JTDINnjIfiVmxWC9tjMwGYfWxBoOSKQfIC1vKredtcUbDH8iUhAt6gXVm1TcxQO9BuWGPjTcXou8E9zRyULvblHJK8OmpGuoz8AulZCwFWzvATPVdntvF9YlPNga6cMDzPBD/XANqQIH+mnG12xTjsCD/CNgl+7osg1YBbVkCRtmaTZxqssf5uFnnues2iyWVoBy4yFIp7XVFkElYzYEN1Nr0N5krgFCO8/c6qP00Ed47J+Cj+LORyR8BD5a1w1I02w6C/8NzrNr4HfmPkXgo/OelSlWdp+z69huYDP9wIG7ufpmD2IS2Hqj265qbf3o3tGPw+QqtS/czhUaWeijPa7b86petC6oO5sw+3YvK98d0vRkIR31kMb+I4T08x7S4KCnyL0vpJ8fFaQNlK87aH8JSB+Y68WOuR6QA148zGBDyH9hY32d+N/V+sf/s9Z3ih58U/TclDG/FLwyUZa0ylFlLjLeiuJ6Lipne7SmrrYcotiEKSUGftTThcSaqlU9GU0tHbV0aWoJs19BKQpH19TK7iTe4C0re5OtU+ehieq+yRwHnvFygB+cz2+BomRz3dsqdwjGP7fOL1aCt6weYHj2W2WnSHu84yUcPTKuNlgpNLRfwpGjkcycdg7PcEvGan14flO9b2gl9f28pRmcDe9o5TS9xcwDsV/bzqPDwpAEyfBPdDJ21yF/NIbvAT7aFpmTNfxteP92aWUf7Y8rrdylKj631e6MoguU9RtXXfi2b9JzWwLPqHneL5hpZllkdh6zxDNbLef3q5bA63SrZXY0sO6Tib6uenyw/ryV2fHk7INiGfTXgydg59nx2HlTG3s8e+PQO9HaOD8es++je3RCW5L9S7e82wvuXLp53/LS7c1sJpnSdje/YdQXbF//Rq6/ZPZCcvQ3cnfZ7Zjr5vN+y9M9k+4Z9jvg5n6z4w7eHNwR5JbFws7mdsoHu+XJ73lBkJ/wlmdxPNlq/4bglLLVvtn58ZgdzOy5O3+8vfuD+OB3/o/W7h+Ox+4H9wXeOIpPxtD50RylboH34zpZ3amE0mEJ1XcEwzLa9XdLKf1MKc26UlpYDqWdUtlSWt+vlGanXEqL48st/XFrdMLnrfJ4zH5bKQ3GZGcUn4wTquNxwsFdQzR2yWlavT4eq9+C/NFj20UefA2hP3bE3RcRf/mtFeqvZ+lFfn5GL7JzdAnn9os0u6D5RZbbUcNx130KWDi7/B7kv09dT9zTeeZTc8kaPtt+lt39nwynN3RHKhVt1Fv9O35k8hzIcv2YRG4SxYHv4iDRc+xmliS+G2E3ICQK/QgPvx4YWngy/BbVfPLd/fel7/8HUEsHCKNA+swOCQAAWzUAAFBLAQIUABQACAgIAChaLEBFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgAKFosQKNA+swOCQAAWzUAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACmCQAAAAA=" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> Hela filen kan laddas ner här.

Bevis som utgår från distributiva lagen

x(c+d) = xc+xd

Antag att x = a+b och sätt in i uttrycket ovan. 

(a+b)c+(a+b)d

c(a+b)+d(a+b)

ca+cb+da+db

ac+bc+ad+bd     V.S.B.

Läs om distrributiva lagen på wwebbmatte.

Kvadreringsregeln

(a+b)2 = a2+2ab+b2

(a-b)2 =  a2-2ab+b2

Förklaring

(a-b)2 =  
(a-b)(a-b) =
a2-ab-ba+b2 =          ( och ab = ba )
a2-2ab+b2                V.S.B.


Länkar:

Bondestam respektive Wille på Mattecentrum om kvadreringsregeln:

Load video
YouTube
Load video
YouTube



Wikipedia (i utskriftsvänlig version) om kvadreringsregeln, nedan inklippt:

Texten ovan är från Wikipedia och inklippt i en frame

Konjugatregeln

Diagnos 11

Lösningar till diagnos 11

Rättelse: I lösningen till uppgift 6 finns tyvärr inte med att lösningen även har en negativ rot. Detta kommer vi att gå in noggrannare på i avsnitt 1.3 som behandlar andragradsekvationer.

Teori

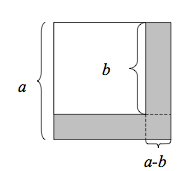
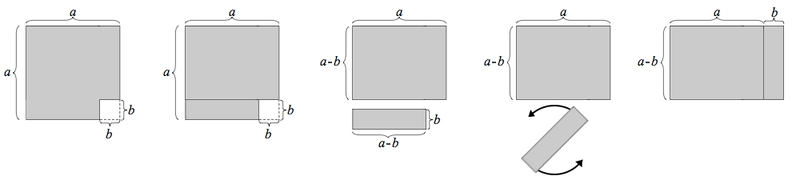
   Så här ser den ut:

   a2-b2 = (a-b)(a+b) 

   utför multiplikationen
   (a-b)(a+b) = a2ab-ba-b2

   (a-b)(a+b) = a2ab-ab-b2

   (a-b)(a+b) = a2b2

   V.S.B.

Länk: engelska Wikipedia

Film

Bondestam (tv) respektive Matteboken (th) förklarar:

Load video
YouTube
Load video
YouTube


Geometriskt bevis av konjugatregeln

Första beviset

Andra beviset

Uppgifter

Khan: Parentesmultiplikation

Hunnet så här långt kan vi repetera genom att lösa lite uppgifter på Khan Academy. De är dels av typen (a+b)(c+d) men också sådana som tillämpar kvadreringsregeln.

Khan om hur man multiplicerar binom ska du verkligen öva på.

Webbmatte

Ekvationer med x2-term

Repetition

Uppgiften från förra lektionen att göra Khan ett tagskulle kunna vara en vettig repetition av föregående vecka.

Intro

Detta avsnitt handlar om ingenting kan man säga. Det handlar nämligen om ekvationer med x2-termer som försvinner vid förenklingen.


Räkna uppgifterna: 1245-1258

  • Uppgift 1251: Här gör du skissen i GeoGebra.
  • Uppgift 1257: Läs om en Ellips på Wikipedia.
    • Pröva att göra en ellips i GeoGebra. Ledining skriv in ekvationen (x/a)^2+(x/b)^2=1. Välj själv värden på a och b.
    • Sök på Ellipse på GeoGebraTube.org.
    • Titta på en ellips i Wolfram|Alpha. Skriv in en formel eller skriv ordet Ellipse.

Övning: Pascals triangel

Gör övningen på sidan 24-25. Titta även på Wikipedia om Pascals triangel.

Andragradsekvationer

Enkla andragradsekvationer

Den här behöver man fundera på en stund. Quadratic equations in early Baghdad

Komplexa rötter

x2 = -16 har ingen reell rot men däremot två komplexa. Det beror på att lösningen är roten ut ett negativt tal. Roten ur -16 är +4i respektive -4i.

x2+3x+16=0 har också två komplexa rötter fast här beror varje rot av både en realdel och en imaginärdel.

Kvadratkomplettering

Uppgift: Khan Academy

Lös dessa Khan, relativt enkla andragradsekvationer. De kan lösas genom att gissa eller faktorisera.

Fullständiga andragradsekvationer

pq-formeln 

x2+px+q=0
x=-p/2+-((p/2)2-q)0.5

Se en film med Michael Bondestam:

Load video
YouTube

Andragradsekvationer och rötter

Komplexa tal

Rotekvationer

Problemlösning med ekvationer

Ekvationslösning med faktorisering

Uppdelning i faktorer med konjugatregeln

Uppdelning i faktorer med kvadreringsreglerna

Faktorisering och ekvationer

Prov

Provet skall vara fredag vecka 6.

(men det kan finnas skäl att ändra det)

Hämtad från ”https://wikiskola.se/index.php?title=Algebra_2C&oldid=11282”