Fysik A

Kollaborativt

http://shareanduse.ning.com/forum/topics/fysiklaerare-anmael-dig-och

http://learnphysics.ning.com/

Laborationer

Laboration - Densitet

Prover att mäta på:

Pb, Al, Fe, Cu, Sn, Zn, Bu, metallcylinder, sten.

Enhetsomvandlingar:

1 ml = 1 cm3 = 10-6 m3
1000 kg/m3 = 1 g/cm3

Sidor i formelsamlingen: 45, 68, 81.

Tabell: densitet

Bedömningsmatris

Laboration Tyngdaccelerationen

Tempograf

• Linköpings Universitet
• Fysikum Stockholms Universitet. Detta kompendium innehåller en mängd varianter för att mäta tyngdaccelerationen.
• Labinstruktion på Malmö Högskola
• Åsö Gymnasium

Bedömning: Bedömningsmatris för tyngdaccelerationslabben.

Problem med felaktigt resultat på tyngdaccelerationen

Dessa två olika vt-diagram illustrerar hur man med samma mätdata kan få två olika resultat beroende på hur man gör.

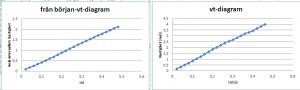
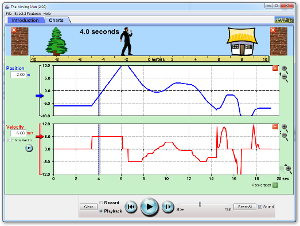
Här är två vt-diagram. Det till vänster ger fel värden på tyngdaccelerationen. I korthet beror det på att man använder hastigheter baserat på intervallet från början till mätpunkten. Det blir som att använda medelhastigheten. Jämför med uttrycket s = at²/2 vilket ger att a = 2 s/t².

Man måste jobba med delta s och delta-t för att det ska funka. Se diagrammet till höger

Laboration 3 Friktion

Bedömning:

Vecka 34-35 - Intro

lektion 1 - Introduktion

Fy A Kursplan från Kursinfo

Min kursplanering delas ut.

Fysik A på Wikibooks

Åtta labbar. Fem godkända för att få godkänt. Dela ut labben om densitet med läxa att plugga på inför nästa vecka.

Bestäm när vi ska labba i halvklass enligt schemat. Dela klassen i två halvor enligt klasslistan.

Att dela ut: böcker, formelsamlingar, labbar, kurplaneringar

Lektion 2 - Vad är fysik, sid 6-8, sid 9-11

Vi ska helt kort diskutera några begrepp som berörs i boken.

Läxa: Detta avsnitt får ni läxa att läsa till nästa gång.

Fysikaliska modeller

Vardaglig förståelse:

Det krävs en kraft för att driva något framåt i en konstant fart.

Newtons andra lag

En kraft som verkar på ett föremål leder till en accelererad rörelse.

Utvecklingen av fysikaliska modeller

Modellen prövas om och om igen. Om den stämmer blir modellen mer etablerad. om den inte stämmer får ma nundersöka mera. Antingen har försöket gjorts fel eller så måste modellen förkastas. Men ofta leder det till att man ger modellen ett tillägg. E

Vatten fryser vid noll.
Men om det är salt sjunker fryspunkten.

Pendellaboration i datorn: PhET Colorado

Det här är en simulering av en pendel. Man kan variera längd och massa på pendel samt variera utslagsvinkeln. Detta är en fysikalisk modell. Undersök modellen och ta reda på hur pendelns längd, massa och vinkel påverkar svängningstiden (peerioden).

Den enkla modellen T = 2 pi rot(l/g) är en förenkling och approximation av sin(täta) = täta. Den fungerar för små vinklar, jmf wikipedia.

Utveckla modellen: Man kan koppla på friktion och variera gravitationen.

Dokumentation

Experiment

Fysik och andra vetenskaper

Reflektera: Skriv svar på frågorna på sid 11. Fundera, diskutera och skriv utförligt.

Formelhantering

Visa formelhantering.

U =R*I, I = U/R. Vilken är den tredje variabeln utlöst.

Gör övningsblad i formelhantering fr Åkes mappar.

Lektion 3 - Snabblabb med pendel och jobb med enheter och prefix

Testa modellen: Jämför med verkliga tyngder/pendel. Exempel på google docs.

Den intresserade läser gärna Pendulum Mathematics

Läs mer: Wikipedia om Pendeln och engelska versionen Dokumentation: Beskriv detta i ord. Rita grafer i Excel om du hinner.

Först en kort labb där alla får testa modellen från Colorado mot verkliga pendlar.

Redovisning i Excel

Sedan genomgång om:

’’’SI-enheterna’’’’ Wikipedia: http://sv.wikipedia.org/wiki/SI-enheter

’’Prefix’’’ Se wikipedia: http://sv.wikipedia.org/wiki/SI-prefix Mätnoggrannhet och värdesiffror. Väresiffror är det antal siffror du får vid en avläsning eller mätning. Ex 3,14 har tre värdesiffro. Räknam med många decimaler ända tills du ska presntera svaret. Då använder du så många värdesiffror som det är i ditt minst noggranna utgångsvärde. Lös uppgifter: sid 16, 20, 22, 23. Läxa;: Sid 12-23 (om man tar med förra läxan)

• Densitet
• Mätnoggrannhet och värdesiffror
• Problemlösning

Jobba

• Läs texten inklusive exemplen på sid 12-19.
• Reflektera sida 21
• Jobba själva med uppgifter i boken sid: 16, 20, 22, 23
• Övningsblad på att byta till SI-enhet, mm.

Läxa tom sid 20

Vecka 36-38: Rörelse

Lektion 4 - Rörelse

Vi behöver jobba färdigt med SI-enheter, sid 21-23.

Länkar

Hastighet enligt Wikipedia

Innehålll

Föremål i rörelse

Film Min film men pingisbollen på Youtube: http://www.youtube.com/watch?v=OYuJXnwDPIE. Men det blir bättre med MovieMaker för där visas tiden i hundradelar.

Beskriv rörelsen med ord Beskriv diagrammet Försök Göra en kurva med hastigheten.

Förklara hur man går till väga när man räknar ut hastigheten med hjälp av mätpunkter i Excel.

Hur långt hann vi? DEDT10 han göra v-t-kurvor men vi hann inte med att diskutera dem. Ska de vara räta eller ... ? Samma ungefär med NV, dock ej vt-kurvor alls.

Ventenskapshistoria

• Nicolaus Copernicus, 19 February 1473 – 24 May 1543)
• Tycho Brahe, (14 December 1546 – 24 October 1601),
• Galileo Galilei, 15 February 1564– 8 January 1642
• Johannes Kepler, December 27, 1571 – November 15, 1630)
• Sir Isaac Newton (25 December 1642 – 20 March 172

Länkar

• http://en.wikipedia.org/wiki/Timeline_of_classical_mechanics
• http://en.wikipedia.org/wiki/Newtonian_physics
• http://en.wikipedia.org/wiki/Physics
• http://en.wikipedia.org/wiki/History_of_classical_mechanics
• http://en.wikipedia.org/wiki/Isaac_Newton
• http://sv.wikipedia.org/wiki/Isaac_Newton

Film

• Genier, Darwin, Newton, mm 88 min. Bara på dvd.
• Den rörliga jorden, 51 min.

Lektion 5 - Medelhastighet, vektorer mm

Addition av vektorerna u och v. CC By

Projicera rutnätet för att rita vektorer

• Repetera S-t-diagram och medelhastighet s 24-26, 30-32. Vi tittat på våra diagram från filmen. Vi räknar ut medelhastigheten ∆s/∆t.

vm = ∆s/∆t

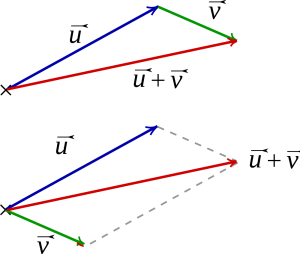
• Hastighet som en vektor, s 28-29.
  • Fart är hur fort det går i vardagligt tal.
  • Hastigheten har en storlek och en riktning. Den ritas som en vektor.
• Vektorer kan adderas och subtraheras.
  • PPT om vektorer som presenterar bokens exempel med fågeln.
• Gör arbetsblad vektorer. Formelsamlingen sid 13 definierar trigonometrin f rätvinklig triangel.
  • Resultant och komposant

Film

• Isaac Newton och gravitationen - Milstolpar inom naturvetenskap och teknik, 15 min. Den börjar med de gamla grekerna, uppehåller sig länge vid Newton och berör Einstein. TEDT hann inte se den.

Gör den här övningen med vektorer!

Lektion 6 - Hastighet

Sträcka-tid-diagram ser ut så här:

Repetition: Forts genomgång av extrabladet om vektorer.

Idag gör vi sid 30-32.

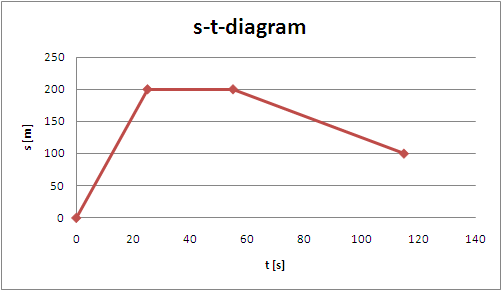
Sträcka-tid-diagram

Att utläsa hastigheten ur diagram.

• ∆s
• ∆t
• v_m = ∆s/∆t (som vi vet sedan tidigare)
• brantare lutning är högre hastighet
• vågrät = stillastående
• avtagande lutning betyder att färden går tillbaks

Bokens Exempel 3.5: Gå igen detta och förklara vad en tangent är. En applet förklarar

Uppgifter: Gör uppgifternas 308-312 på sidan 32. Lösning i Excel till uppgift 310

Datorövning: titta på s-t-diagrammet med pingisboleln igen.

1. Excelfil med pingisdata.
2. Beräkna medelhastigehten för hela resan.
3. Hur ändras hastigheten under bollens färd?

Datorövning: Movin Man från PhET Colorado

Click to Run

Lektion 7 - Acceleration och vt-diagram

Bedömningsmatrisen för densitetslabben

Planering: Vi behöver bestämma datum för laborationen om acceleration. Förslag:

TEDT10 onsdag vecka 39 kl 10.40-12.10 Den halvklassgrupp som har operativsystem denna onsdag
TEDT10  onsdag vecka 40 kl 10.40-12.10 Den halvklassgrupp som har operativsystem denna onsdag
NVNV10 tisdag kl 8-9.30 vecka 39. (NV10 ledigt)
NV10 onsdag kl 12.40-14.10 vecka 39. (NVNV10 ledigt)

v 38 Genomgång idag: neXus FYSIK sid S 33-38.

Acceleration

• Medelaccelerationen = ∆v/∆t
  • ∆v = v_efter-v_före
  • ∆t = t_efter-t_före
• Acceleration enligt Wikipedia.
• Gå igenom exempel 3.8 i boken.

Tyngdaccelerationen

• Tyngdaccelerationen är cirka 9,82 m/s² vid jordytan. Eftersom jorden är plattare vid polerna ökar tyngdaccelerationen ju längre norrut vi kommer från ekvatorn.

v-t-diagram

• vt-graf Wikipedia.
  • Här kan man jämföra st- och vt-grafer. Motsvarar Exempel 3.9 i boken.
• Lutningen i vt-diagrammet visar accelerationen:
  • brantare lutning <==> större acceleration
  • lutar "neråt" <==> retardation

Datorövning:

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

• titta på filmen med pingisboleln igen.
• Använd ditt s-t-diagrammet med pingisbollen igen till att skapa ett vt-diagram. Är rörelsen accelererad? Excelfil med pingisdata.
• Räkna ut medelaccelerationen. (Detta motsvarar exempel 3.7)

Mer att titta på:

• Khan Academy om acceleration
• Georgios smedja i matematik och fysik.

Lektion 8 - Begynnelsehastighet

Sträckan = arean under en vt-graf. CC By Tharbad

v 38 Idag: Sid 39-44

Laborationsinstruktion: Gå igenom instruktionen till Acceleerationslabben

Begynnelsehastighet och förändring av hastigheten

Acceleration är lika med hastighetsökningen per sekund. Vid en konstant acceleration a, gäller då att:

v = v0 + at

v₀ är hastigheten vid start och t är så klart tiden från start.

Exempel: Fru Gran tapper en blomkruka genom fönstret. Vilken hastighet har den 1,5 sekunder senare?

t = 1,5 s. a = g = 9,82 m/s2. 
v = at = 9,82 m/s2 * 1,5 s = 14,7 m/s

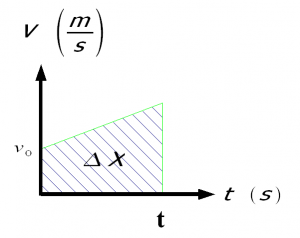
area

Arean under en vt-graf är lika med sträckan. Tänk att medelhastigheten * tiden = sträckan.

vm = (vefter - vföre) / 2 

Men sträckan är ju v_m * t och det kan man ju se som arean av cen triangel som bildas av grafen i vt-diagrammet.

naturvetenskap.org ger en beskrivning.

Animering av sträcka under vt-kurva <swf width="600" height="400">/images/FysikA_s_e_area_u_vt_kurva_2.swf</swf>

uppgift 320 b, c, d

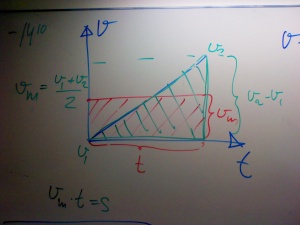
sträcka

Härled uttrycket nedan som på sidan 41.

s = v0t + at2/2

Extrablad: Rörelselära ... Och Övningsuppgifter på hastighet och fart.

v 39

Sid 45-53

Uppgifter: 320-327

Vecka 40-42 - Newtons kraftlagar

Planeringen måste tryckas ihop för vi ligger efter i tid. Friktionslabben måste skjutas på eller utgå.

Vi ska göra friktionslabben men inte i halvklass utan under lektionen.

Lektion 9 - Krafter: Newtons tre kraftlagar

Newtons tre kraftlagar. CC By

v 40 neXus FYSIK A: Sidorna 54-62.

Newton

Newton kuinde bygga visdare på Keppler mfl och förklara fysiken bakom planeternas banor.

Krafter

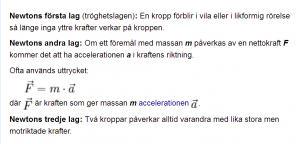
Newtons första lag

Newtons andra lag

Click to Run

Enheten Newton

Tyngdkraft

F = mg

Newtons tredje lag

Click to Run

Lektion 10 - Gravitationskraft, friktion och fjäderkonstant

v 40

neXus FYSIK A: Sidorna 63-69.

Dagens tre formler finns i formelsamlingen på sidan 44.

Gravitationskraften

Click to Run

Friktionskraft

F = μ * FN
där F är friktionskraften, μ är friktionskoefficienten och N är Normalkraften.

Normalkraften är lika med tyngdkraften i många fall.

Fjäderkonstant

Formeln som beskriver kraften som förlänger fjädern kallas Hookes lag.

F = k * ∆l
där F är fjäderkraften, k är fjäderkonstanten och ∆l är förlängningnen av fjädern

neXus FYSIK A: Sidorna 65-69.

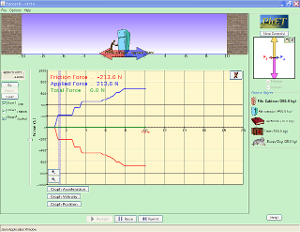
PhET Colorado om fjäderkonstant och friktion

lektion 11 - Kraftmoment och jämvikt

Kraften i punkt B ger ett större vridmoment på muttern än samma kraft i punkt A. [CC http://commons.wikimedia.org/wiki/File:Torque.JPG By]

En kloss i vila på på ett lutande plan. CC By

Ta med: balansvåg med vikter, linjal och tyngder.

v 41

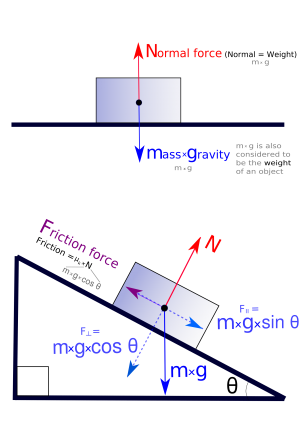
neXus Fysik A sid 68: Tyngdkraftens komposanter på ett sluttande plan.

neXus FYSIK A: Sidorna 70-74.

Förra gången: Men kanske först något om tyngdkraften (och dess komposanter) när en bok exempelvis ligger på ett lutande plan och jämvikt råder mellan tyngdkrafter och friktionskraften.

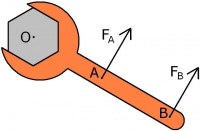
Kraftmoment

M = F * l
F är kraften, l är det vinkelräa avståndet mellan kraften och rotationscentrum
l kan ses som avståndet till kraftens angreppspunkt men då får man räkna med den vinkelräta komposanten

Teori: Wikipedia om Kraftmoment. OBS! Wikipoedia anvender begreppet vridmoment med bokstaven τ istället.

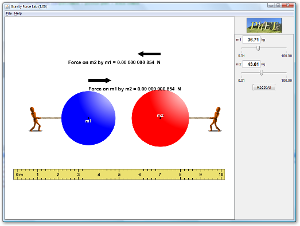
Demo: Walter Fendt - The Lever

Demo: Riktig balansvåg...

Jämvikt

Om summan av alla krafter samt kraftmoment som verkar på ett föremål är noll då är föremålet i jämvikt.

Wikipedia har en bra bild på kraftjämvikt för kloss på lutande plan.

Sammanfattning och repetition

v 41

neXus FYSIK A: Sidorna 75-78.

Diverse i slutet kapitlet

neXus FYSIK A: Sidorna 79-81.

Fundera och diskutera

Prova själv

Berg- och dalbanor

Krockar

Extra

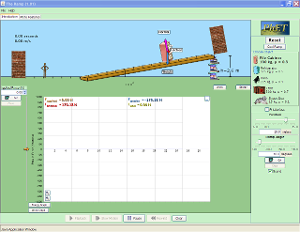
The Ramp nedan skulle vara bra men den funkar för närvarande inte på min dator.

Click to Run

Film

• http://www.sli.se/prodinfo.asp?sid=a1a52336-9fe5-4613-ac0f-6521f7bd4973&a=DVD+2021. Newton, mekanik, energi, muskler, mm.
• http://learnphysics.ning.com/video/newtons-laws-of-motion-1
• http://learnphysics.ning.com/video/dropping-a-feather-and-a

Extra

Fysik för under f Euro Fasta nyckeln och gemet. Gausskanonen.

Prov - kapitel 1-4, ons v 42

v 42

Energi

Kionetisk energi