Fysikuppgifter på de fyra systemen: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) |
||
| (40 mellanliggande sidversioner av samma användare visas inte) | |||
| Rad 3: | Rad 3: | ||
=== Lyft stenen === | === Lyft stenen === | ||
[[Fil:hävstång.jpg|right| | {{uppgfacit|'''Hävstång och sten''' | ||
[[Fil:hävstång.jpg|right|300px]] | |||
Om man tar ett spett som är 1 meter långt och sätter spetsen under en sten och sedan sätter en sten 1 decimeter från spetsen så har man fått en utväxling på 1:9, vilket innebär att spettets spets om man trycker nedåt med 650 Newton på spettets andra ände utsätter stenen för en större kraft. Hur stor är kraften på stenen? | Om man tar ett spett som är 1 meter långt och sätter spetsen under en sten och sedan sätter en sten 1 decimeter från spetsen så har man fått en utväxling på 1:9, vilket innebär att spettets spets om man trycker nedåt med 650 Newton på spettets andra ände utsätter stenen för en större kraft. Hur stor är kraften på stenen? | ||
| | |||
: <math>F = 9 \cdot 650 N = 5850 N</math> | |||
Om man jämför kraftmomenten ser man att: | |||
: <math>F_1 l_1 = F_2 l_2</math> | |||
: <math>F_2 = \frac{l_1 }{l_2 }F_1 = \frac{9 }{1 } 650 </math> | |||
<math>F_1 </math> och <math>l_1 </math> är i detta fallet kraften på den långa delen av spettet till höger i bild | |||
}} | |||
{{clear}} | {{clear}} | ||
=== Uppgift med besman === | === Uppgift med besman === | ||
{{ | {{uppgfacit | '''Väg med ett besman''' | ||
[[Fil:Besman (ur Nordisk familjebok).png| left |300px|Besman]] | [[Fil:Besman (ur Nordisk familjebok).png| left |300px|Besman]] | ||
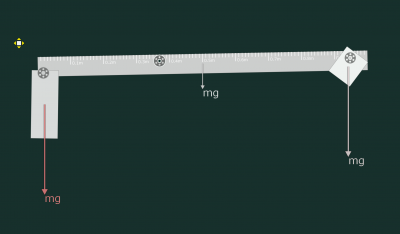
Ett besman enligt figuren består av en en meter lång stång med en centimeterskala. Stången väger 0,4 kg. I stångens ena ände hänger man det man det föremål som ska vägas och i den andra änden sitter en 1.5 kg tung metallklump. Skalan visar att den korta delen (A-C) är 37 cm. Vad väger föremålet. | Ett besman enligt figuren består av en en meter lång stång med en centimeterskala. Stången väger 0,4 kg. I stångens ena ände hänger man det man det föremål som ska vägas och i den andra änden sitter en 1.5 kg tung metallklump. Skalan visar att den korta delen (A-C) är 37 cm. Vad väger föremålet. | ||
| | |||
[[Fil:Besman.PNG|400px|höger]] | |||
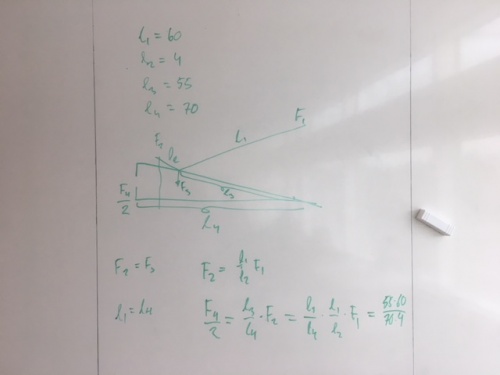
Ställ upp kraftmomenten för den okända vikten, stångens vikt samt tyngden i högra änden. Observera att vi räknar med masscentrum för stången i mitten av stången. | |||
: <math> m_1</math> sökes, <math> l_1 = 0.37~m</math> | |||
: <math> m_2 = 0.4 ~kg</math>, <math> l_2 = 0.13~m</math> | |||
: <math> m_3 = 1.5 ~kg</math>, <math> l_3 = 0.63~m</math> | |||
Eftersom besman-vågen är i balans är kraftmomentet <math> M_1</math> på vänster sida lika stort som de två <math> M_2 + M_3</math> på höger sida. | |||
: <math> m_1 l_1 = m_2 l_2 + m_3 l_3</math> | |||
När vi löser ut : <math> m_1</math> får vi | |||
: <math> m_1 = \frac{m_2 l_2 + m_3 l_3}{l_1} = \frac{0.4 \cdot 0.13 + 1.5 \cdot 0.63}{0.37} = 2.7 kg</math> | |||
}} | }} | ||
{{clear}} | {{clear}} | ||
| Rad 24: | Rad 53: | ||
=== Bilens vrid === | === Bilens vrid === | ||
{{uppgfacit|'''Vridmoment''' | |||
I en Volvo V70 har motorn ett vridmoment på 330 Nm. Växellådan växlar ner varvtalet med förhållandet 1:1.7. Vilken kraft ger däcket mot asfalten? sök lämpliga fakta som behövs för uppgiftens lösande på internet och ange dessa i redovisningen. | I en Volvo V70 har motorn ett vridmoment på 330 Nm. Växellådan växlar ner varvtalet med förhållandet 1:1.7. Vilken kraft ger däcket mot asfalten? sök lämpliga fakta som behövs för uppgiftens lösande på internet och ange dessa i redovisningen. | ||
| | |||
Mekanikens gyllene regel gäller här. Det man vinner i varvtal förlorar man i kraftmoment (kraft). | |||
: Fakta: <math>M_d = 330 Nm</math> | |||
: Kraftmoment: <math>M_d= \frac{1}{1.7} \cdot M_m</math> | |||
Beteckningen på ett ganska typiskt bildäck är 225/55 R 17 97 W vilket kan ge oss information om hjulets radie. En sida med hjälp att [https://www.bfgoodrich.se/se/raad/Daeckfakta/Vad-betyder-markeringarna-paa-daecksidan tolka beteckningar på däck] anger att fälgen är 17 tum och däckets höjd är 55 % av bredden 225 mm. | |||
Däckets diameter är då: | |||
: <math> 2(225 \cdot 0.55)+17 \cdot 25.4 = 680~mm </math> | |||
: och <math> r = 340~mm </math> | |||
: <math> F = \frac{M_d}{r} = \frac{330}{1.7 \cdot 0.34} = 570 N </math> | |||
}} | |||
=== Uppgift kraftmoment === | === Uppgift kraftmoment === | ||
{{ | {{uppgfacit| '''Hur fungerar det mekaniska systemet nagelklipparen''' | ||
[[File:Coupe ongle.png| right | 300px | Coupe ongle]] | |||
En nagelklippare består av två skänklar med tänder vilka klipper av nageln från båda hållen. Skänklarna kläms ihop genom att en hävstång verkar på båda skänklarna genom en stång. | |||
Vilken utväxling får man med denna nagelklippare? Totala längden är cirka 7 cm. | Vilken utväxling får man med denna nagelklippare? Totala längden är cirka 7 cm. | ||
| Rad 35: | Rad 86: | ||
Använd figuren och sätt ut relevanta mått och krafter. | Använd figuren och sätt ut relevanta mått och krafter. | ||
| | |||
[[ | [[Fil:Tk2 IMG 2038.JPG|500px]] | ||
}} | }} | ||
{{clear}} | {{clear}} | ||
=== Friktion === | === Friktion === | ||
{{uppgfacit|'''En bil''' | |||
[[Fil:Static friction flat.jpg |400px|right| Krafter vid friktion.]] | [[Fil:Static friction flat.jpg |400px|right| Krafter vid friktion.]] | ||
Bilen på bilden väger 1240 kg. Friktionstalet är 0.13. Hur mycket väger tyngden om bilen | Tänk dig en bil som glider på grus eller is. | ||
Bilden föreställer en bil som dras av kraften från en tyngd men det skulle kunna vara en bogsering eller något annat. | |||
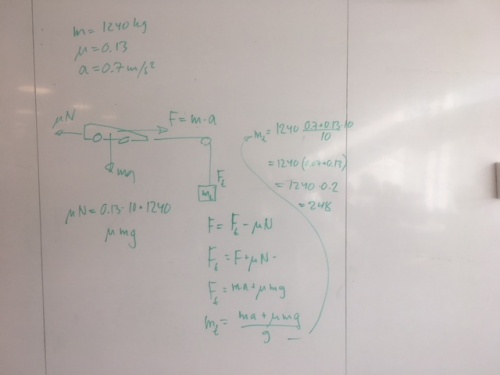
Bilen på bilden väger 1240 kg. Friktionstalet är 0.13. Hur mycket väger tyngden om bilen accelererar med 0.7 m/s<sup>2</sup>? | |||
| | |||
[[Fil:IMG_2039.JPG|500px]] | |||
Bilen påverkas av tre krafter. En bromsande friktionskraft <math>F_{friktion}</math>, en dragkraft från tyngden <math>F_{tyngd}</math> samt en resulterande accelererande kraft <math>F_{a}</math>. Krafterna balanserar varandra så att | |||
<math>F_{friktion} + F_{a} = F_{tyngd}</math> | |||
: Friktionskraften beror på friktionstalet och normalkraften: <math>F_{friktion} = \mu N</math> där <math>N = mg</math>. | |||
: Dragkraften beror på tyngdaccelerationen som verkar på bilens massa: <math>F_{tyngd} = m_2 g</math> | |||
: Den resulterande kraften ger upphov till en acceleration hos bilen: <math>F_{a} = m a</math> | |||
}} | |||
{{clear}} | {{clear}} | ||
=== Verkningsgrad i vattenkokare === | === Verkningsgrad i vattenkokare === | ||
{{ | {{uppgfacit|'''Vattenkokaren''' | ||
En vattenkokare hemma är märkt med effekten 1520 Watt. Det tar 130 s att värma 0.5 l 22-gradigt vatten till kokning. Vad har den för verkningsgrad. | En vattenkokare hemma är märkt med effekten 1520 Watt. Det tar 130 s att värma 0.5 l 22-gradigt vatten till kokning. Vad har den för verkningsgrad. | ||
| | |||
'''Fakta:''' | |||
: <math>P=1520 ~W,~ t=130 ~s,~ m=0.5 ~kg,~ c=4.19 \cdot 10^3~J/(kg K),~ \Delta T = 100-22~C</math> | |||
'''Formler:''' | |||
: <math>\eta = \frac{W_{nyttig}}{W_{tillförd}}</math> | |||
Tillförd energi {{=}} Elektrisk energi: | |||
: <math>W_{tillförd}= P \cdot t </math> | |||
Nyttig energ {{=}} uppvärmningen av vattnet: | |||
: <math>W_{nyttig}= c \cdot m \cdot \Delta T </math> | |||
: <math>\eta = \frac{4190 \cdot 0.5 \cdot 78}{1520 \cdot 130} = 0.83 = 83~\%</math> | |||
}} | }} | ||
| Rad 65: | Rad 150: | ||
=== Praktisk ellära för husägare === | === Praktisk ellära för husägare === | ||
{{uppgfacit |'''Stoppa tjuven''' | |||
# Tag reda på vad enheten Amperetimmar innebär. | # Tag reda på vad enheten Amperetimmar innebär. | ||
# vad är en kilowattimme. | # vad är en kilowattimme. | ||
# | # Vilken lampa ska man välja för att stoppa tjuven? | ||
Vilken lampa ska man välja för att stoppa tjuven? | |||
Du tänker ha en lampa (inne i huset) som tänds med automatik på kvällarna när du inte är på ditt landställe. Avsikten är att lura tjuvarna att tro att det är någon där. | Du tänker ha en lampa (inne i huset) som tänds med automatik på kvällarna när du inte är på ditt landställe. Avsikten är att lura tjuvarna att tro att det är någon där. | ||
| Rad 94: | Rad 177: | ||
: Konventionella lampans ström: <math> I_k = \frac{P}{U} = \frac{60}{230} = 260 mA</math> | : Konventionella lampans ström: <math> I_k = \frac{P}{U} = \frac{60}{230} = 260 mA</math> | ||
Tag sedan reda på priset per kilowatttimme och beräkna kostnaden per år för respektive lampa. | |||
}} | }} | ||
=== Ellära i GeoGebra === | === Ellära i GeoGebra === | ||
Dra i reglagen i figuren och betrakta grafen. Vad betyder lutningen? | |||
{{clear}} | |||
<html> | <html> | ||
<iframe scrolling="no" src="https://tube.geogebra.org/material/iframe/id/1065885/width/635/height/370/border/888888/rc/false/ai/false/sdz/true/smb/false/stb/false/stbh/true/ld/false/sri/true/at/auto" width="635px" height="370px" style="border:0px;"> </iframe> | <iframe scrolling="no" src="https://tube.geogebra.org/material/iframe/id/1065885/width/635/height/370/border/888888/rc/false/ai/false/sdz/true/smb/false/stb/false/stbh/true/ld/false/sri/true/at/auto" width="635px" height="370px" style="border:0px;"> </iframe> | ||
</html> | </html> | ||
{{uppgfacit| '''Max effekt''' | |||
Välj lämpliga värden på spänning och resistans. Vilken är den maximal effekt systemet utvecklar och vad blir det av effekten? | |||
| | |||
Maximal effekt får vi med de högsta värdena på spänning och ström, dvs: | |||
: <math> P = U \cdot I = 12 V \cdot 60 A = 720 W </math> | |||
Det är ungefär en hästkraft och motsvarar den effekt man får i startmotorn till en bil. I detta fall här vi en resistans som värms upp. I startmotorns fall omvandlas effekten genom elektromagneterna i motorn till vridmoment och mekanisk effekt. | |||
}} | |||
=== Lyfta bilen === | === Lyfta bilen === | ||
I en hydraulisk | {{uppgruta| | ||
I en hydraulisk domkraft har den lyftande pistongen diametern 3.5 cm och den kan lyfta 1.5 ton. Hur stor skulle den pistongen kunna vara och hur stor kraft behövs för att få max lyftkraft? | |||
}} | |||
=== Hydraulisk press === | === Hydraulisk press === | ||
{{uppgruta| | |||
Tag reda på fakta om [https://www.biltema.se/bil---mc/verkstadsutrustning/lyftutrustning/verkstadspressar/verkstadspress-10-ton-2000040920 pressen] och utför några lämpliga beräkningar. | Tag reda på fakta om [https://www.biltema.se/bil---mc/verkstadsutrustning/lyftutrustning/verkstadspressar/verkstadspress-10-ton-2000040920 pressen] och utför några lämpliga beräkningar. | ||
}} | |||
Nuvarande version från 26 november 2018 kl. 19.32
Lyft stenen
Facit: (klicka expandera till höger)
- [math]\displaystyle{ F = 9 \cdot 650 N = 5850 N }[/math]
Om man jämför kraftmomenten ser man att:
- [math]\displaystyle{ F_1 l_1 = F_2 l_2 }[/math]
- [math]\displaystyle{ F_2 = \frac{l_1 }{l_2 }F_1 = \frac{9 }{1 } 650 }[/math]
[math]\displaystyle{ F_1 }[/math] och [math]\displaystyle{ l_1 }[/math] är i detta fallet kraften på den långa delen av spettet till höger i bild
Uppgift med besman
Facit: (klicka expandera till höger)
Ställ upp kraftmomenten för den okända vikten, stångens vikt samt tyngden i högra änden. Observera att vi räknar med masscentrum för stången i mitten av stången.
- [math]\displaystyle{ m_1 }[/math] sökes, [math]\displaystyle{ l_1 = 0.37~m }[/math]
- [math]\displaystyle{ m_2 = 0.4 ~kg }[/math], [math]\displaystyle{ l_2 = 0.13~m }[/math]
- [math]\displaystyle{ m_3 = 1.5 ~kg }[/math], [math]\displaystyle{ l_3 = 0.63~m }[/math]
Eftersom besman-vågen är i balans är kraftmomentet [math]\displaystyle{ M_1 }[/math] på vänster sida lika stort som de två [math]\displaystyle{ M_2 + M_3 }[/math] på höger sida.
- [math]\displaystyle{ m_1 l_1 = m_2 l_2 + m_3 l_3 }[/math]
När vi löser ut : [math]\displaystyle{ m_1 }[/math] får vi
- [math]\displaystyle{ m_1 = \frac{m_2 l_2 + m_3 l_3}{l_1} = \frac{0.4 \cdot 0.13 + 1.5 \cdot 0.63}{0.37} = 2.7 kg }[/math]
Övningsuppgift från Provbanken NP Fysik A vt-2005
Bilens vrid
Facit: (klicka expandera till höger)
Mekanikens gyllene regel gäller här. Det man vinner i varvtal förlorar man i kraftmoment (kraft).
- Fakta: [math]\displaystyle{ M_d = 330 Nm }[/math]
- Kraftmoment: [math]\displaystyle{ M_d= \frac{1}{1.7} \cdot M_m }[/math]
Beteckningen på ett ganska typiskt bildäck är 225/55 R 17 97 W vilket kan ge oss information om hjulets radie. En sida med hjälp att tolka beteckningar på däck anger att fälgen är 17 tum och däckets höjd är 55 % av bredden 225 mm.
Däckets diameter är då:
- [math]\displaystyle{ 2(225 \cdot 0.55)+17 \cdot 25.4 = 680~mm }[/math]
- och [math]\displaystyle{ r = 340~mm }[/math]
- [math]\displaystyle{ F = \frac{M_d}{r} = \frac{330}{1.7 \cdot 0.34} = 570 N }[/math]
Uppgift kraftmoment
Friktion
Facit: (klicka expandera till höger)
Bilen påverkas av tre krafter. En bromsande friktionskraft [math]\displaystyle{ F_{friktion} }[/math], en dragkraft från tyngden [math]\displaystyle{ F_{tyngd} }[/math] samt en resulterande accelererande kraft [math]\displaystyle{ F_{a} }[/math]. Krafterna balanserar varandra så att
[math]\displaystyle{ F_{friktion} + F_{a} = F_{tyngd} }[/math]
- Friktionskraften beror på friktionstalet och normalkraften: [math]\displaystyle{ F_{friktion} = \mu N }[/math] där [math]\displaystyle{ N = mg }[/math].
- Dragkraften beror på tyngdaccelerationen som verkar på bilens massa: [math]\displaystyle{ F_{tyngd} = m_2 g }[/math]
- Den resulterande kraften ger upphov till en acceleration hos bilen: [math]\displaystyle{ F_{a} = m a }[/math]
Verkningsgrad i vattenkokare
Facit: (klicka expandera till höger)
Fakta:
- [math]\displaystyle{ P=1520 ~W,~ t=130 ~s,~ m=0.5 ~kg,~ c=4.19 \cdot 10^3~J/(kg K),~ \Delta T = 100-22~C }[/math]
Formler:
- [math]\displaystyle{ \eta = \frac{W_{nyttig}}{W_{tillförd}} }[/math]
Tillförd energi = Elektrisk energi:
- [math]\displaystyle{ W_{tillförd}= P \cdot t }[/math]
Nyttig energ = uppvärmningen av vattnet:
- [math]\displaystyle{ W_{nyttig}= c \cdot m \cdot \Delta T }[/math]
- [math]\displaystyle{ \eta = \frac{4190 \cdot 0.5 \cdot 78}{1520 \cdot 130} = 0.83 = 83~\% }[/math]
Pentryfysik
| Uppgift |
|---|
| Mikrovågsugnen
Gå till pentryt och koka ett par dl vatten i mikrovågsugnen och beräkna verkningsgraden. Gör lämpliga antaganden och sök den information du behöver. Det ingår i uppgiften att klura ut ett enkelt sätt att mäta vattnets temperatur.
|
Praktisk ellära för husägare
Facit: (klicka expandera till höger)
Om värmen är avstängd väljer vi naturligtvis lågenergilampan som förbrukar mindre energi eftersom den drar mindre ström.
Om vi däremot har huset uppvärmt kanske valet blir en konventionell glödlampa som är billigare i inköp. Den lampan har lägre verkningsgrad vilket innebär att en stor del av energin blir värme istället för ljus. Denna värme bidrar till uppvärmningen och blir därmed nyttig i alla fall.
Spänningen i vägguttaget är 230 V
- Lågenergilampans ström: [math]\displaystyle{ I_l = \frac{P}{U} = \frac{14}{230} = 61 mA }[/math]
- Konventionella lampans ström: [math]\displaystyle{ I_k = \frac{P}{U} = \frac{60}{230} = 260 mA }[/math]
Tag sedan reda på priset per kilowatttimme och beräkna kostnaden per år för respektive lampa.
Ellära i GeoGebra
Dra i reglagen i figuren och betrakta grafen. Vad betyder lutningen?
Facit: (klicka expandera till höger)
Maximal effekt får vi med de högsta värdena på spänning och ström, dvs:
- [math]\displaystyle{ P = U \cdot I = 12 V \cdot 60 A = 720 W }[/math]
Det är ungefär en hästkraft och motsvarar den effekt man får i startmotorn till en bil. I detta fall här vi en resistans som värms upp. I startmotorns fall omvandlas effekten genom elektromagneterna i motorn till vridmoment och mekanisk effekt.
Lyfta bilen
| Uppgift |
|---|
|
I en hydraulisk domkraft har den lyftande pistongen diametern 3.5 cm och den kan lyfta 1.5 ton. Hur stor skulle den pistongen kunna vara och hur stor kraft behövs för att få max lyftkraft? |
Hydraulisk press
| Uppgift |
|---|
|
Tag reda på fakta om pressen och utför några lämpliga beräkningar. |