Beräkning av gränsvärden: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
Hakan (diskussion | bidrag) |
||
| (4 mellanliggande sidversioner av samma användare visas inte) | |||
| Rad 1: | Rad 1: | ||
{{lm3c | En kurvas lutning |120 - 124}} | {{lm3c | En kurvas lutning |120 - 124}} | ||
{{clear}} | |||
{{#ev:youtube | tgZ-DEo3ty4 | 340 | | {{#ev:youtube | tgZ-DEo3ty4 | 340 | left | Beräkning av gränsvärden. Frökenfysik, YT-licens}} | ||
{{#ev:youtube | Bexr07IesNw | 340 | right | Beräkning av gränsvärden. 7:17 min. Åke Dahllöfk, YT-licens}} | {{#ev:youtube | Bexr07IesNw | 340 | right | Beräkning av gränsvärden. 7:17 min. Åke Dahllöfk, YT-licens}} | ||
| Rad 18: | Rad 18: | ||
: <math> \lim_{x \to 2} \frac{x^2 - 2^2}{x - 2} = \lim_{x \to 2} \frac{(x + 2)(x - 2)}{x - 2} = \lim_{x \to 2} (x + 2) = 4 </math> | : <math> \lim_{x \to 2} \frac{x^2 - 2^2}{x - 2} = \lim_{x \to 2} \frac{(x + 2)(x - 2)}{x - 2} = \lim_{x \to 2} (x + 2) = 4 </math> | ||
}} | }} | ||
== Numerisk beräkning av gränsvärden == | |||
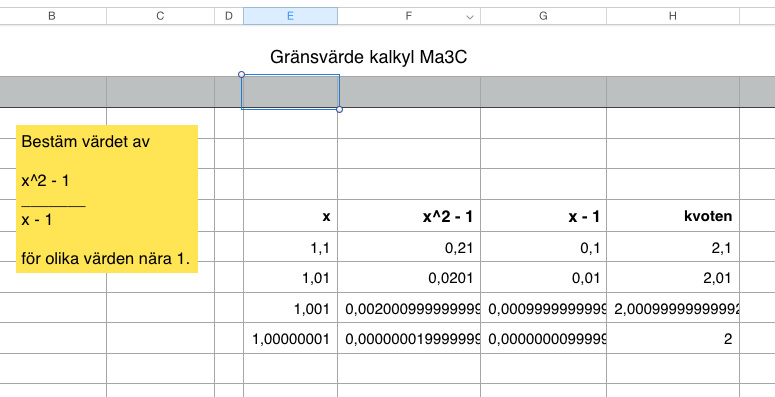
Många gånger kan det löna sig att använda ett kalkylprogram om man vill se hur ett uttryck närmar sig gränsvärdet. Här syns ett exempel i Numbers: | |||
[[Fil:Skärmavbild 2016-02-06 kl. 02.01.18.png|left]] | |||
{{clear}} | |||
== Fördjupning == | == Fördjupning == | ||
Nuvarande version från 6 februari 2016 kl. 01.09
| Definition |
|---|
Gränsväde i en punkt
|
| Exempel |
|---|
| Beräkna gränsvärdet algebraiskt
Vad är gränsvärdet för [math]\displaystyle{ \.. \frac{x^2 - 4}{x - 2} }[/math] om [math]\displaystyle{ x }[/math] går mot 2 ?
|
Numerisk beräkning av gränsvärden
Många gånger kan det löna sig att använda ett kalkylprogram om man vill se hur ett uttryck närmar sig gränsvärdet. Här syns ett exempel i Numbers:
Fördjupning
Rita grafen för funktionen [math]\displaystyle{ f(x) = (1 + \frac{1}{x})^x }[/math] och uppskatta gränsvärdet för [math]\displaystyle{ \lim_{x \to \infty} f(x) }[/math]
