Dataövning - konsekutiva tal: Skillnad mellan sidversioner

Nuvarande version från 7 februari 2018 kl. 07.08

Flipped lesson: arbeta igenom innehållet till nästa lektion innan lektionen. Det vinner du på!

Ma2C: Konsekutiva tal, sidan 57

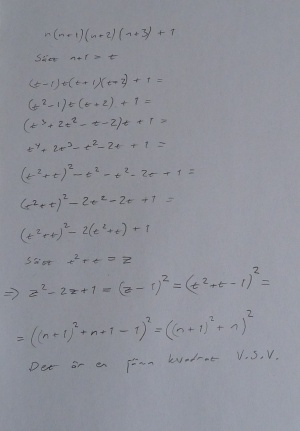
Börja med att använda ett kalkylprogram för att pröva hur uppgifterna stämmer för några olika tal. Använd formler.

Del ett Visa att roten ur ett plus produkten av ett tal och samma tal plus två är ett heltal.

Ledning: (n-1)(n+1)+1

Del två

Visa att roten ur produkten av fyra konsekutiva tal plus ett är ett heltal.

Del tv är svårare. Det handlar om fyra konsekutiva tal. Addera ett till produkten av de fyra talen och ta roten ur. Detta ska bli ett heltal.

Wolfram|Alpha har en lösning men ingen förklaring.
Med hjälp av den ledtråden från Wolfram ser min lösning ut så här.
Tanja löser uppgiften genom att pröva.
Fredrik använder kvadratkomplettering och substitution för att lösa uppgiften. Lösningen syns i bilden till höger.
Charlie i NV11 löser det genom att hitta mönster i de tal han prövar med och ...

@@ Rad 2: / Rad 2: @@
 [[Fil:Fredrik_problem_konsekutiva_tal.jpg|300px|right|Fredriks lösning.]]
-'''Del ett''' (n-1)(n+1)+1
+Börja med att använda ett kalkylprogram för att pröva hur uppgifterna stämmer för några olika tal. Använd formler.
+'''Del ett'''
+Visa att roten ur ett plus produkten av ett tal och samma tal plus två  är ett heltal.
+Ledning: (n-1)(n+1)+1
 '''Del två'''
+Visa att roten ur produkten av fyra konsekutiva tal plus ett är ett heltal.
 Del tv är svårare. Det handlar om fyra konsekutiva tal. Addera ett till produkten av de fyra talen och ta roten ur. Detta ska bli ett heltal.