Lektion 6 Sinussatsen: Skillnad mellan sidversioner
Hoppa till navigering
Hoppa till sök
Hakan (diskussion | bidrag) (Skapade sidan med ' {{#ev:youtube|R1Sjs8FIu38|240|right|Sinussatse}} 300px <math>\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} </math> === Hä...') |
Hakan (diskussion | bidrag) |
||
| (10 mellanliggande sidversioner av samma användare visas inte) | |||
| Rad 1: | Rad 1: | ||
{{flipp}} | |||
{{#ev:youtube|R1Sjs8FIu38|240|right|Sinussatse}} | |||
{{#ev:youtube| wBTe_xo1G8E |240|right|Sinussatse, av Åke Dahllöf.}} | |||
{{ | {{defruta | Sinussatsen | ||
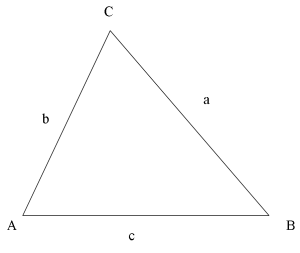
[[Fil:Triangle_ABC_with_Sides_a_b_c.png|300px]] | [[Fil:Triangle_ABC_with_Sides_a_b_c.png|300px]] | ||
<math>\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} </math> | <math>\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} </math> | ||
}} | |||
=== Härledning === | === Härledning 1 === | ||
# Ställ upp areasatsenför alla tre vinklar. | # Ställ upp areasatsenför alla tre vinklar. | ||
| Rad 10: | Rad 14: | ||
# Dividera med abc | # Dividera med abc | ||
<br /> | <br /> | ||
=== Härledning 2 === | |||
<div style="float:right;margin:0 0 1em 1em;">[[Fil:Law of sines proof.svg]]</div> | |||
Antag en triangel med sidorna ''a'', ''b'' och ''c'' och med de motstående vinklarna ''A'', ''B'' och ''C''. En linje med längden ''h'' och vinkelrät mot sidan ''c'' är dragen från hörnet ''C'' till motstående sida ''c'' eller sidan ''c'':s förlängning. | |||
Då är | |||
:<math>\sin A = \frac{h}{b}</math> | |||
och | |||
:<math>\; \sin B = \frac{h}{a}</math> | |||
Vilket är ekvivalent med | |||
:<math>h = b\,\sin A = a\,\sin B</math> | |||
och | |||
:<math>\frac{\sin A}{a} = \frac{\sin B}{b}</math> | |||
Om linjen dras mellan vinkeln ''A'' och sidan ''a'' och samma procedur upprepas blir resultatet | |||
:<math>\frac{\sin B}{b} = \frac{\sin C}{c}</math> | |||
{{svwp|sinussatsen}} | {{svwp|sinussatsen}} | ||
<br /> | <br /> | ||
{{Läxa|Lös uppgifterna 1414- | |||
== Kunskapskontroll == | |||
<html> | |||
<iframe src="https://docs.google.com/forms/d/1jMvctF7DQpm58aRJoXjr1WuBvn95q7l-VkCrwCaB06I/viewform?embedded=true" width="760" height="500" frameborder="0" marginheight="0" marginwidth="0">Loading...</iframe> | |||
</html> | |||
== Räkna alla uppgifterna == | |||
{{Läxa|Lös uppgifterna 1414-1427 på sidan 28 och gärna fler. | |||
}} | }} | ||
{{clear}} | {{clear}} | ||
== Fördjupning - Sinussatsen == | |||
[[Fördjupning - Sinussatsen]] med uppgifter från gamla NP. | |||
Nuvarande version från 15 september 2015 kl. 10.39
| Definition |
|---|
| Sinussatsen
|
Härledning 1
- Ställ upp areasatsenför alla tre vinklar.
- Förläng med 2.
- Dividera med abc
Härledning 2
Antag en triangel med sidorna a, b och c och med de motstående vinklarna A, B och C. En linje med längden h och vinkelrät mot sidan c är dragen från hörnet C till motstående sida c eller sidan c:s förlängning.
Då är
- [math]\displaystyle{ \sin A = \frac{h}{b} }[/math]
och
- [math]\displaystyle{ \; \sin B = \frac{h}{a} }[/math]
Vilket är ekvivalent med
- [math]\displaystyle{ h = b\,\sin A = a\,\sin B }[/math]
och
- [math]\displaystyle{ \frac{\sin A}{a} = \frac{\sin B}{b} }[/math]
Om linjen dras mellan vinkeln A och sidan a och samma procedur upprepas blir resultatet
- [math]\displaystyle{ \frac{\sin B}{b} = \frac{\sin C}{c} }[/math]
Wikipedia skriver om sinussatsen
Kunskapskontroll
Räkna alla uppgifterna
Fördjupning - Sinussatsen
Fördjupning - Sinussatsen med uppgifter från gamla NP.