Introduktion till induktion samt demonstration: Skillnad mellan sidversioner
Hakan (diskussion | bidrag) |
Hakan (diskussion | bidrag) Ingen redigeringssammanfattning |
||
| (13 mellanliggande sidversioner av samma användare visas inte) | |||
| Rad 1: | Rad 1: | ||
{| class="wikitable" | |||
|- | |||
! Digital bok !! Pappersbok | |||
|- | |||
| {{Gleerups| [https://gleerupsportal.se/laromedel/impuls-2/article/9a2b6bc7-6f4d-43ba-b68a-30f98d07a90e Induktion] [https://gleerupsportal.se/laromedel/impuls-2/article/8882c005-152f-4081-9b2b-90107609c92c Uppgifter Induktion]}} || {{Heureka2| Kap 6 Sid 106-112}} | |||
|} | |||
{{clear}} | |||
== Introduktion == | == Introduktion == | ||
{{#ev:youtube|-UzfQqJTZto|320|right | Praktisk demonstration av induktion.}} | {{#ev:youtube|-UzfQqJTZto|320|right | Praktisk demonstration av induktion.}} | ||
| Rad 61: | Rad 67: | ||
== Lenz lag == | == Lenz lag == | ||
Tillämpning av industriell betydelse: [[Teslas_induktionsmotor|Teslabilarnas induktionsmotor]] | |||
[[Fil:Lenz lag.png|340px|miniatyr|höger|Den inducerade strömmen ger upphov till en motriktad kraft på ledaren. Det krävs alltså en kraft (=arbete) för att röra den med jämn fart i magnetfältet.]] | [[Fil:Lenz lag.png|340px|miniatyr|höger|Den inducerade strömmen ger upphov till en motriktad kraft på ledaren. Det krävs alltså en kraft (=arbete) för att röra den med jämn fart i magnetfältet.]] | ||
Ledarens rörelse i magnetfältet ger upphov till en inducerad ström i den yttre slingan men eftersom det är en sluten krets fortsätter den strömmen även genom ledaren i magnetfältet. Då har vi den välbekanta situationen med en elektrisk ledare i ett magnetfält. Det ger upphov till en kraft som vi sett tidigare. Denna kraft är motriktad kraften som skapar ledarens rörelse. Det måste uträttas ett arbete för att skapa strömmen. | |||
För att röra ledaren med en konstant hastighet så krävs e kraft som är lika stor och motriktad den kraft som uppstår på grund av Lenz lag. Om det inte krävdes en kraft för att röra ledaren skulle man ju generera ström utan att arbete utfördes (en evighetsmaskin). | |||
Strömmen i ledaren kan också förklaras som att det är strömmen av laddningar som förskjuts när den inducerade spänningen skapas. | |||
{{clear}} | |||
== Magnetsikt flöde == | == Magnetsikt flöde == | ||
| Rad 81: | Rad 95: | ||
<br /> | <br /> | ||
<math> | : <math>\Phi = B A </math> | ||
<br /> | |||
\Phi = B A | |||
: <math>\Delta \Phi = B \Delta A </math> | |||
\Delta \Phi = B \Delta A | <br /> | ||
: <math>\Delta \Phi = B \Delta s \cdot l </math> | |||
\Delta \Phi = B \Delta s \cdot l | <br /> | ||
: <math>\Delta \Phi = B v \Delta t \cdot l </math> | |||
\Delta \Phi = B v \Delta t \cdot l | <br /> | ||
: <math>\Delta \Phi = B l v \Delta t </math> | |||
\Delta \Phi = B l v \Delta t | <br /> | ||
: <math>\Delta \Phi = e \Delta t </math> | |||
\Delta \Phi = e \Delta t | <br /> | ||
: <math>\Leftrightarrow</math> | |||
\Leftrightarrow | <br /> | ||
: <math> e = \frac{\Delta \Phi}{\Delta t} </math> | |||
e = \frac{\Delta \Phi}{\Delta t} | |||
</math> | == Lästips == | ||
: [http://olleh.se/start/teori/teori-induktion.htm Olle H] | |||
: [http://www.bjornjonsson.se/pdf/fybmagnlekt06.pdf Fy B Björn Jonsson] | |||
Nuvarande version från 15 november 2017 kl. 12.25
| Digital bok | Pappersbok |
|---|---|
Introduktion
Om en elektrisk ledare förflyttas i ett magnetfält uppstår en spänning och man kan generera ström. Detta kallas induktion.
Det är fysik med många nyttiga tillämpning i bland annat elektriska motorer och generatorer.
Induktion
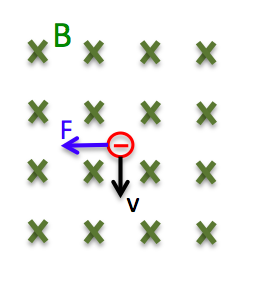
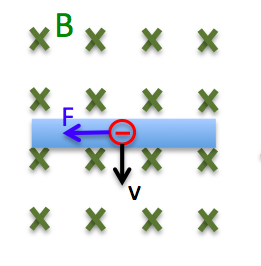
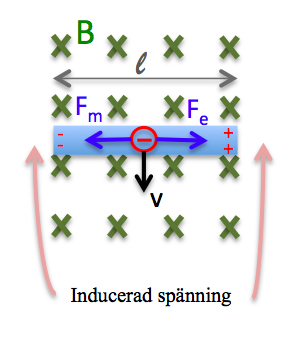
En ledare förflyttas i ett magnetfält. Om man ser till en laddning i ledaren så förflyttas den nedåt i bilden och vi har en laddning med en hastighet i ett magnetfält. Den påverkas således av en vinkelrät kraft. I det här fallet påverkas elektroner av en kraft till vänster i bilden och positiva laddnings påverkas av en kraft till höger. Detta gör att laddningarna förskjuts åt sidorna vilket ger upphov till ett elektriskt fält i ledaren och en elektromotorisk spänning (ems, e).
Om ledaren förflyttas med jämn fart uppstår en balans mellan de elektriska och magnetiska krafterna.
Kraften från det magnetiska fältet.
- [math]\displaystyle{ F_B = q v B }[/math]
Kraften från det elektriska fältet ges av:
- [math]\displaystyle{ F_E = q E }[/math]
När krafterna är i balans fås:
- [math]\displaystyle{ q E= q v B }[/math]
eller
- [math]\displaystyle{ E= v B }[/math]
Det elektriska fältet kan skrivas som:
- [math]\displaystyle{ E = U / d = e / l }[/math]
Vilket ger:
- [math]\displaystyle{ e = l B v }[/math]
Inducerad ström

Den inducerade spänningen ger upphov till en inducerad ström om ledaren ingår i en sluten krets.
Så länge man rör ledare kommer det att drivas fram nya elektroner i den del av ledaren som befinner sig i magnetfältet. En kontinuerlig rörelse ger en kontinuerlig ström.
Strömmen går åt samma håll i den slutna kretsen vilket innebär att den går från minus till plus i den delen av ledaren. I den yttre delen av kretsen går strömmen som brukligt från plus till minus.
Lenz lag
Tillämpning av industriell betydelse: Teslabilarnas induktionsmotor
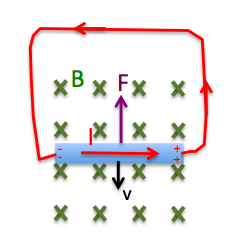
Ledarens rörelse i magnetfältet ger upphov till en inducerad ström i den yttre slingan men eftersom det är en sluten krets fortsätter den strömmen även genom ledaren i magnetfältet. Då har vi den välbekanta situationen med en elektrisk ledare i ett magnetfält. Det ger upphov till en kraft som vi sett tidigare. Denna kraft är motriktad kraften som skapar ledarens rörelse. Det måste uträttas ett arbete för att skapa strömmen.
För att röra ledaren med en konstant hastighet så krävs e kraft som är lika stor och motriktad den kraft som uppstår på grund av Lenz lag. Om det inte krävdes en kraft för att röra ledaren skulle man ju generera ström utan att arbete utfördes (en evighetsmaskin).
Strömmen i ledaren kan också förklaras som att det är strömmen av laddningar som förskjuts när den inducerade spänningen skapas.
Magnetsikt flöde
B känner vi ju som magnetsk flödestäthet. Det är alltså areaberoende.
magnetskt flöde definieras som
- [math]\displaystyle{ \Phi = B A }[/math]
Där A är arean.
Enheten för magnetiskt flöde är T m2 eller Weber, Wb.
Induktionslagen på annan form
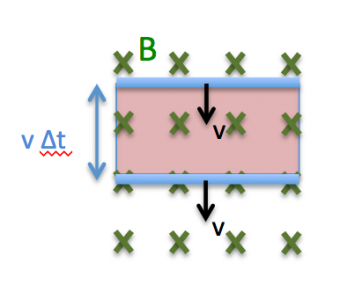
- [math]\displaystyle{ \Phi = B A }[/math]
- [math]\displaystyle{ \Delta \Phi = B \Delta A }[/math]
- [math]\displaystyle{ \Delta \Phi = B \Delta s \cdot l }[/math]
- [math]\displaystyle{ \Delta \Phi = B v \Delta t \cdot l }[/math]
- [math]\displaystyle{ \Delta \Phi = B l v \Delta t }[/math]
- [math]\displaystyle{ \Delta \Phi = e \Delta t }[/math]
- [math]\displaystyle{ \Leftrightarrow }[/math]
- [math]\displaystyle{ e = \frac{\Delta \Phi}{\Delta t} }[/math]
