Heureka 8.10: Skillnad mellan sidversioner
Jakob (diskussion | bidrag) Ingen redigeringssammanfattning |
Jakob (diskussion | bidrag) Ingen redigeringssammanfattning |
||
| (3 mellanliggande sidversioner av samma användare visas inte) | |||
| Rad 4: | Rad 4: | ||
[[Fil:Fysik uppgift 8,10.jpeg]] | [[Fil:Fysik uppgift 8,10.jpeg]] | ||
Hur löser vi denna uppgift? | |||
Vi kan använda oss Kirchhoffs första lag säger att strömmarna som går in i en förgrening är lika stora som strömmarna som går ut ur förgreningen. | |||
Alltså kan vi addera strömmen som vi får och därmed kan vi räkna ut I. | |||
I uppgift A ska vi addera 2.0+0.5 A och ta slutsatsen att strömmen är 2.5 A åt höger. | |||
I uppgift B är precis likadan som uppgift A men stömmarna är rikdade åt vänster. | |||
I uppgift C så har vi en 2.0 ut från kretsen och en 0.5 in samt en okänd krets. Vi kan använda Kirchhoffs första lag igen och ränka ut den okända värdet på I. | |||
2.0-0.5=1.5=I. Svar: 1.5 A med rikning åt vänster. | |||
Grattis du löst 8.10, du är nu lite smartare och kan fortsätta dina studier genom att fortsätta in på 8.11. Bra jobbat och lycka till! | |||
Nuvarande version från 9 januari 2014 kl. 12.46
Denna Sida är uppfunnen av Jakob Johannesson torsdagen den 9/1-2014
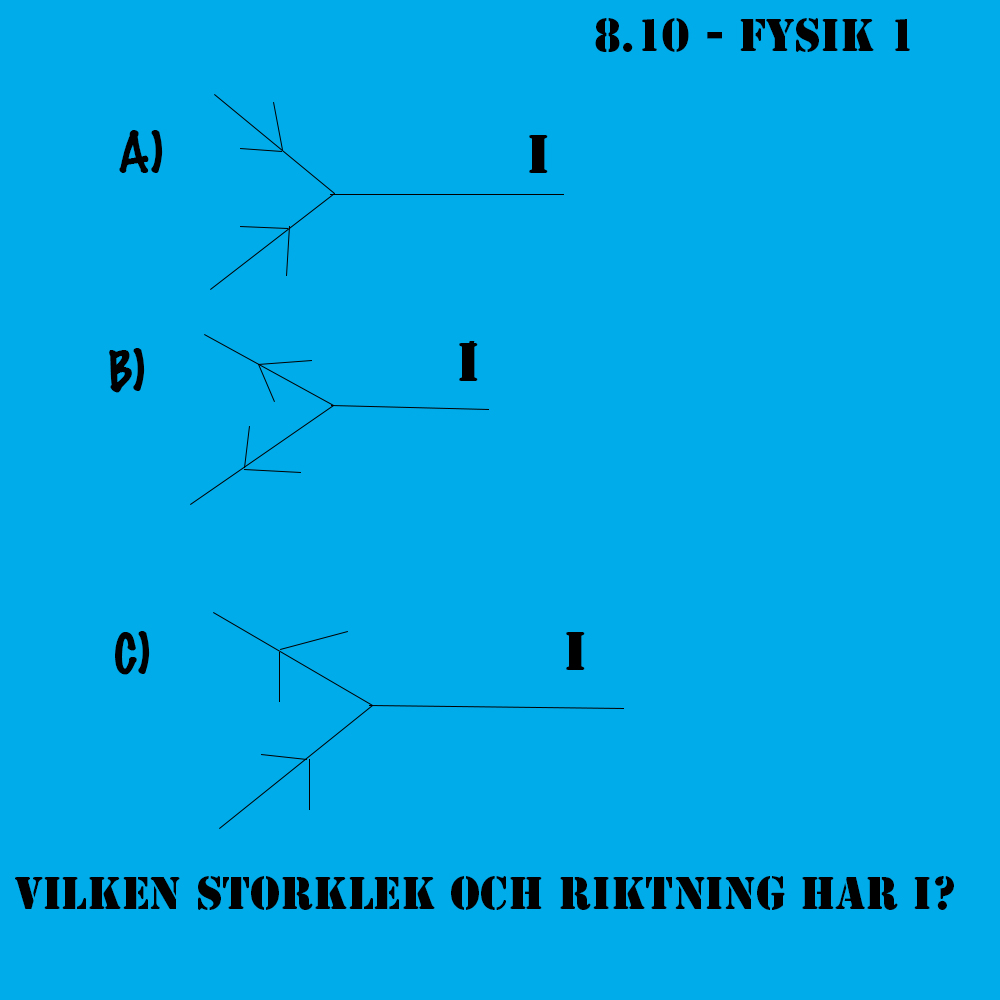
Bestäm strömmen I till storlek ock riktning i följande fall:
Hur löser vi denna uppgift?
Vi kan använda oss Kirchhoffs första lag säger att strömmarna som går in i en förgrening är lika stora som strömmarna som går ut ur förgreningen.
Alltså kan vi addera strömmen som vi får och därmed kan vi räkna ut I.
I uppgift A ska vi addera 2.0+0.5 A och ta slutsatsen att strömmen är 2.5 A åt höger.
I uppgift B är precis likadan som uppgift A men stömmarna är rikdade åt vänster.
I uppgift C så har vi en 2.0 ut från kretsen och en 0.5 in samt en okänd krets. Vi kan använda Kirchhoffs första lag igen och ränka ut den okända värdet på I. 2.0-0.5=1.5=I. Svar: 1.5 A med rikning åt vänster.
Grattis du löst 8.10, du är nu lite smartare och kan fortsätta dina studier genom att fortsätta in på 8.11. Bra jobbat och lycka till!