Konjugatregeln: Skillnad mellan sidversioner

Från Wikiskola
Hoppa till navigering Hoppa till sök
Visuell
 
(10 mellanliggande sidversioner av 2 användare visas inte)
Rad 1: Rad 1:


=== Konjugatregeln ===
=== Konjugatregeln ===
{{lm2c|Konjugatregeln|22-24}}


    Så här ser den ut:
:  Så här ser den ut:
 
    a<sup>2</sup>-b<sup>2</sup> = (a-b)(a+b)  
:    a<sup>2</sup>-b<sup>2</sup> = (a-b)(a+b)
   
    utför multiplikationen:
:   <math> (a-b)\cdot(a+b) </math>  
    (a - b)(a + b) = a<sup>2</sup> + ab - ba - b<sup>2</sup>
    vi kan stryka ab - ba = ab - ab = 0:
    (a - b)(a + b) = a<sup>2</sup> - b<sup>2</sup>
    V.S.B.


=== Konjugatregeln med &lt;math&gt; <math>\LaTeX</math> &lt;/math&gt; ===
:  <math>= a^2 +a\cdot b -a\cdot b -b^2 </math>
:
:  vi kan stryka ab - ba = ab - ab = 0:


    Så här ser ''beviset'' ut:
:   <math>= a^2-b^2 </math>
   
   
    <math>(a-b)\cdot(a+b) </math>
:    V.S.B.
    <math>= a^2 +a\cdot b -a\cdot b -b^2 </math>
    <math>= a^2-b^2 </math>
    <math>\blacksquare</math>


=== Film ===
=== Film ===
Rad 55: Rad 44:
   Denna är gjord med Geogebra, sparad som animerad gif, upladdad till WIKIMEDIA COMMONS och länkad hit.
   Denna är gjord med Geogebra, sparad som animerad gif, upladdad till WIKIMEDIA COMMONS och länkad hit.
   
   
   (a-b)(a+b) = a&#178; - b&#178;</p>
   <math>(a - b)\cdot(a + b) = a^2 - b^2 </math>


<applet name="ggbApplet" code="geogebra.GeoGebraApplet" archive="geogebra.jar"
<html>
codebase="http://jars.geogebra.org/webstart/4.2/unsigned/"
<iframe scrolling="no" src="https://tube.geogebra.org/material/iframe/id/390017/width/1188/height/912/border/888888/rc/false/ai/false/sdz/true/smb/false/stb/false/stbh/true/ld/false/sri/true/at/auto" width="1188px" height="912px" style="border:0px;"> </iframe>
width="1669" height="929">
</html>
<param name="ggbBase64" value="UEsDBBQACAgIACeiY0IAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAAnomNCAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbN1c23LbNhq+bp8Cw53JNLsRjRNPidyOkzpOZpO2U2c7O3sHiZDEiCK1JGXLmTzHPkH3vu1FHyC57zPtD4CUSB1sSZZreZNIIEic/u8/4ieU9jfTUYwuZJZHaXJsERtbSCbdNIyS/rE1KXot3/rm6y/bfZn2ZScTqJdmI1EcW9ym1rwf1GzKVOcoPLZ6vZCKkPmtnhBui3sObQlMwxYhQUi8gElHQmc0zaOnSfqdGMl8LLryvDuQI/Em7YpCjzkoivHTo6PLy0u7mt1Os/5Rv9+xp3loIVh5kh9b5cVTGK7R6ZLp5hRjcvTPt2/M8K0oyQuRdKWFFFWT6Osvv2hfRkmYXqLLKCwGgIEbuBYayKg/ADoJZlA7Us3GQO1YdovoQubQuVbVVBejsaWbiUQ9/8JcoXhGkIXC6CIKZXZsYZsAEJQ71GeY+L7rWyjNIpkUZVtSznlUjda+iOSlGVZd6Rk5DjxgQpRHnVgC7CLOga4o6WWAKSwom0A1L65i2RFZVZ+vhzyBv9Ag+iDVWMA8AwRUAvyEcvLEw/iJw3yzlvrEFirSNNajYuQE6ONHRDHF6IkqiCkoFK5rHmFzDzNTUFNwUzimDTfduWnKTRtu2nB2DZ1lfU5oeaNBaUUnq9NJgD71ceGjAVig06/RSRQRHxFRq9cFQ2rdRK9fFbysuqbq6YJgU5Dyoa++NF7uLSliO1FEarMaedhm0mpKwl2++Zx0izkXZXRGJV1FJXXWUHlLcGd0OrVJYS79T3+WpmR0mymXVHGHGRULdtf9HSb0cEPtK503JSnL62DY26LaR5U1bJcLQvlAtS3Fq5CjXC2RBdo4IYIcUF7XA1viIBJA4Sklpog4iDtQJT5yVekhpvSWI4Z8pNoRhrQJcnz44lqnXeTAWOqmZ5QbMY4chog2XBwBCkgbP8CEMmjhOMiBTmp2oqZlLuIuVJiPOCxQmT1PmRYG/aAOk1PECGKqL/EQdZFLkadMJ+HKorq+WjsMSpGLkau6gu0Eu2lsJvTwEVPUgBaM0zyagTuQ8XjGFY1jlIwnRYldeb87Cisci3SheZh2h88XwJYiL6praAQea+4XjQdruM0v2rHoyBjCi3MlBwhdiFipuR6/lyYFqmSAmnv9TIwHUTc/l0UBvXL0XlyIN6KQ05fQOq8WqKfW/rwtJ904CiOR/ARCooZQA6KZe9e2q3LvAQ7MNN00zcLzqxxEB03/JbMUTI5vB/U/joWuzBMeuM1HMGLeFUrmedB84gMTrtY888zU8mJGm5jKGUWon+lgal55nT9P4/mtcRolxQsxLiaZjtbAVmaKqpOkH0uNruY6xD3dYSednhtYmRnr3dUYatisoNN/kcZphkAnqQNk9suyY0rdRi1t1grrNli3wBWfonD2nARUt9Blx5S6FTDeLK0klVRkElxNE+Xa2sDgDbnUYqOCqEkSFW+qShF1h3NSVYfvJqMOSFxNLmqDkr0N2j5aELO2iHWMWgmdmEyjOBLZVV1bdMdGw/ZQZomMjQgmIAWTdJIbpagRMMnlD6IYnCThj7IP6vyDUBa1gCWZptXgoKKyG42go7lfoi6URPwDSDR3Q9nPZAWNWYzhiX6K6wqxdFsP9TJLR6+Ti3cgbgtLbR9V9LTzbhaNlVijDpj4oZwLbhjlAhxEWO8HxOdARVcZK2BAocAfpsn7SV8UmezLOLGQmBSDFKTr1P47DAImAGQevRUAAsUg1zqUT7NhPpCyeCenBRKd9AIafSVancdfib91HqNjJD79hlqo8+k3EEwZK858/s9FAssEu/b00V8Ifqa/ZA/QRSEopkCw/QCwsygfCugD7g0NRQJuDmWffx4mYt6JPAbvEjA0VWGtB5N9o2/Tx+jN599zNP30WyuAuxj1Pv8OeiJlHAt08fnnLJQJGn/+L5ra88FWfZ3/dPIjeorMZI2ZOMIY609LeZVj8GBgYVDgEA2vjOUIdheo0GqvLcdM+k80ckpKUdp5D5Z65pnN85ocwvOVNkBbCxGPB0LtbUpRicUVQFiXQz3g2zRcFCmQWM13sL5jo3NjKY26mgXDxRiG02authwto4Cr2rgysMFXMJPtgsX9YLayZtumiFXGz0zq1O/OxZuWSm1wugGx5/8HiDm2QzVizN4PYN10NBJJiBId6/2Qxlf9NLHmUYbAStSQIAo/JKjaRhqIJkX1vOxFTDNhmnWgYMdWFwoOxgsK59h6AYV7bH1rVlHOvYJtZhUVY2bjN31RAQHGEPbZud6sFKVr1BevohCUU+F5tBPPK39a+co5z+kSz8l6nq+XzFz2VW22DrGbbK5f57Js4utkcy5hLWwHRim5TXwtY63A9p2A1MKjxbBgc1aA2MRKvl8nyg9K7TmWPedQyrGKdb5P3mUiyVX6qukyN0e2c8/IziOKBZ9fgxyQ9hrhp8ZfcYItxrLADura3PGceWvnAbGjewM75vjsgxvf93q5LDTGBtPVBpptzKpFluiNwmoOftB7EUocUrt734wCWmDroXyQvi22Y154X8wjxum1nFuyb5FNgR52iancmD3fJpjM9SzgB8c+FRNvEwK9WGZgc0+1moMq0d03RccUd2gNue0YXfVsb4VOrQt42OqA5wY/3ITn2wcAD7Y5rv8hngbLtf2mr9gLWIvRoQKrGRuKpWjw9Kbgro746R5icszvNyYHgWXcgT2b63CHE+KXATrzfA7s8Zmr3xV5f1q8frpZvE5NM2ma9Uy83jfx+sDE6y9NvH62U7xO/7x4fb083FG8LnfyhNuI7Wo7wVaE6xRijMCnxGU+IYxwWjk13+GY+yCb3PF95UKVU6M2o5wyh3JwaASuD86r3eDRFlnRu19WbBLfL/HCqwL8Ju+oZyJ816bMA6NBXcd1wbgspWEfGIv6d2/lb+9WF9SoiuwXeYeZZhGYd86ZyzzssQDCxPsP7Tdnx+AhsGPZel2t4ZKyag5stDwMTzA8c1zOD3lP3AyBXj6AoBPgDerBjFcmiJwGk+idB+hnDwArbjNCg8ANeIA9gM11SrDAWvjYBfyIy0tDv9/4/LzU82Y0WGZvz5bCwOj6qG7RakQ3Yb+B2dhPhpLYHq5Byct8GbUDrwH8zDa41MEeGGmXBAyi8oMyDU0Wvo3C8Ypd1pnh4ckSD19ts9l6dd/aM+chtSG4AcYB9xwGF6zcMzmEBJgxHIAdZ3eiJG+jLEuz1TumV0v4vt4G39e74UuoyY/pcoOXTBtCTGzYitY3oNV7I95wrPwOjLZ+3Tyj+o9fNS7QcVJ1r2bLY3WyEo2iRGvcSEzV4Y6/fvoFAOjkaTwp5Hk3kzKZHzA1kcrsWAhXx1cVtVhfqUyIvuhFUzk7EjNIs+hDmhRNk73bloHgZVNGNuQR2cHyVIcBsm6NK2uyF4ArUQpFA6qyzhwunOWEBl6V0FivMD+mhSjkgsK8NgrTAt7q7MHzZc15JMZp/mwr/Sm73N7PPEQV2gD1sxtRP9se9bPDQP2gI6uV3Di5kRsn23Pj5DC40Tij0UwsB5ud2Ngj0Kc3An26PdCnhwb0XtLIuyb2V6aRS4TM9mFWoXNDrTPGNSFflWVmZZa53r9f7x/NKhwih80YuTLfzA7ifIizDf+3SDivE9d7PCayKkOznI8uUzQPKkOzlMDcCP39vv6+JumPba8ZlxhH2GI2CRompPSF2PY5JQyQ5xy2VtS9d+i3f5G9lI64B5bUTiTwm4+T7J7NJHaAAz9gHmMQ5NBgl33DIeX/xa187d1Yr5UatEaBWp7yzYEKLjF2fNe7/xcyO74TPikduHG9yznBsjM3rd+b1kPTOjYuerSTc+brnTPbg3PupkkYmZ0wNP++bP3Hr+hRv3iG8Kdf1otV/TcTc9EKlkRrL++N399SB1YvdlkPrlnsLRzJohpcZ5du4Oqf7sKHh4X8xvETxdW5p6ZPuM4EHRr28cFhv5X13yp+OjTsR4eF/Z2+2L0H7KfjDKZWjqeEU/2EiVgIHhxbj/49SYtnJqdxlKUwqzC39DBNvhXQz2oOstNeb/PXbdcejMsLkRX6wB8qs0C0furQcC2weeMuq+cm6jAd1X8opn/zWf7fEF//D1BLBwgKNUdU9AsAAMtCAABQSwECFAAUAAgICAAnomNCRczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIACeiY0IKNUdU9AsAAMtCAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAjAwAAAAA" />
<param name="java_arguments" value="-Xmx1024m -Djnlp.packEnabled=true" />
<param name="cache_archive" value="geogebra.jar, geogebra_main.jar, geogebra_gui.jar, geogebra_cas.jar, geogebra_algos.jar, geogebra_export.jar, geogebra_javascript.jar, jlatexmath.jar, jlm_greek.jar, jlm_cyrillic.jar, geogebra_properties.jar" />
<param name="cache_version" value="4.2.23.0, 4.2.23.0, 4.2.23.0, 4.2.23.0, 4.2.23.0, 4.2.23.0, 4.2.23.0, 4.2.23.0, 4.2.23.0, 4.2.23.0, 4.2.23.0" />
<param name="showResetIcon" value="false" />
<param name="enableRightClick" value="false" />
<param name="errorDialogsActive" value="true" />
<param name="enableLabelDrags" value="false" />
<param name="showMenuBar" value="false" />
<param name="showToolBar" value="false" />
<param name="showToolBarHelp" value="false" />
<param name="showAlgebraInput" value="false" />
<param name="useBrowserForJS" value="true" />
<param name="allowRescaling" value="true" />
Detta är en Java Applet skapad med GeoGebra från www.geogebra.org - det verkar som om du inte har Java installerat på din dator, vänligen besök www.java.com


This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com
[http://www.geogebratube.org/material/show/id/390017 Länk till filen]
</applet>


=== Uppgifter ===
=== Uppgifter ===
Rad 86: Rad 59:
   
   
   2.  Lös  <math>x^2-1=0</math> för alla reella x.
   2.  Lös  <math>x^2-1=0</math> för alla reella x.
  ''Tips : Använd konjugatregeln och nollregeln för ekvationen.''


{{khanruta|'''Khan: Parentesmultiplikation'''  
{{khanruta|'''Khan: Parentesmultiplikation'''  

Nuvarande version från 28 januari 2015 kl. 20.54

Konjugatregeln

Ma2C: Konjugatregeln, sidan 22-24


Så här ser den ut:
a2-b2 = (a-b)(a+b)
[math]\displaystyle{ (a-b)\cdot(a+b) }[/math]
[math]\displaystyle{ = a^2 +a\cdot b -a\cdot b -b^2 }[/math]
vi kan stryka ab - ba = ab - ab = 0:
[math]\displaystyle{ = a^2-b^2 }[/math]
V.S.B.

Film

Bondestam (tv) respektive Matteboken (th) förklarar:

Load video
YouTube
Load video
YouTube


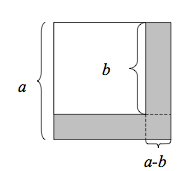
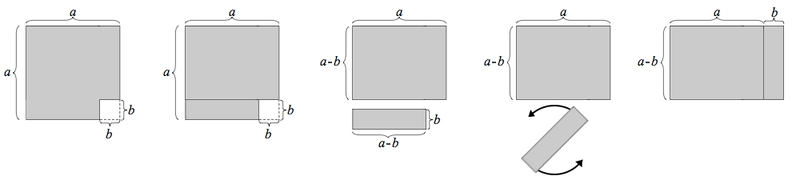
Geometriskt bevis av konjugatregeln

Första beviset

Andra beviset

Visualisering 

  Här gäller:

  [math]\displaystyle{ (x-y)\cdot(x+y) = x^2 - y^2  }[/math]

  Denna är gjord med Geogebra, sparad som animerad gif, upladdad till WIKIMEDIA COMMONS och länkad hit.

  [math]\displaystyle{ (a - b)\cdot(a + b) = a^2 - b^2  }[/math]

Länk till filen

Uppgifter

Övningar (utan räknare) 

  1. [math]\displaystyle{ 1992\cdot 2008 = ? }[/math]

  2.  Lös  [math]\displaystyle{ x^2-1=0 }[/math] för alla reella x.

  Tips : Använd konjugatregeln och nollregeln för ekvationen.
Öva på Khan: Khan: Parentesmultiplikation

Hunnet så här långt kan vi repetera genom att lösa lite uppgifter på Khan Academy. De är dels av typen (a+b)(c+d) men också sådana som tillämpar kvadreringsregeln.

Khan om hur man multiplicerar binom ska du verkligen öva på.


Webbmatte

Hämtad från ”https://wikiskola.se/index.php?title=Konjugatregeln&oldid=30565”